指向直观想象的教学设计

罗成芳

摘 要：本文是以培养数学学科直观想象核心素养为目标，以探讨一元二次方程根的分布为载体进行教学设计。利用方程与函数的关系，数形结合思想，解决根的分布问题。首先，教师引导，建立数与形的关系，渗透直观想象素养;然后，问题深究，巧用直观想象解决问题;最后，问题变式，落实直观想象素养。

关键词：直观想象;一元二次方程;根的分布;教学设计

1教学内容及其解析

1.1 内容

一元二次方程的根分布在一个区间、两个区间的问题

1.2 地位和作用

本节是人教A版必修一《3.1函数与方程》之后的一个专题内容，一元二次方程根的分布问题是高中数学重要的内容。它与二次函数，以及一元二次不等式（必修五第三章）联系密切。本节课是对数形结合思想、函数与方程的思想、零点存在定理的应用，它是研究函数与方程的重要载体，而其中用到的思想方法为进一步学习数学做铺垫。

1.3 思想方法

在讨论根的分布问题用到了数形结合、函数与方程、化归思想

1.4 核心素养

直观想象、逻辑推理、数学运算

1.5 教学重点

基于以上分析，确定本节课的教学重点是利用函数图象求解有关一元二次方程根的分布问题。难点：函数与方程，数形结合思想、直观想象核心素养的渗透。

2教学目标解析

2.1 目标

掌握一元二次方程根的分布問题，会根据函数与方程的关系进行转化，能够解决一些简单的不等式。

2.2 目标解析

正确划分一元二次方程根的分布问题，即分布在同一区间还是不同区间。在方程根的问题转化为函数零点问题过程中体会函数与方程、数形结合思想。

3教学问题诊断分析

3.1 教学的第一个问题可能是在例1思考过程中在想不到利用函数与方程间的关系，将根的分布问题转化为函数与轴的交点问题。

问题解决方案：适当的提醒学生我们可不可以画出图形，接着问画出谁的图形，然而将方程与函数联系起来，将方程根的问题转化为函数与轴的交点问题。

3.2 教学的第二个问题可能是当根分布在两个区间时，学生会类比写出约束条件。

问题解决方案：首先鼓励学生要大胆猜想，提示能否根据二次函数的特点及零点存在定理只需利用区间端点函数值的正负就可以确定函数是有两不同的实数根。

3.3 教学的第三个问题可能是学生无法准确总结出一般结论。

问题解决方案：带动学生去分析、猜想、归纳。根据他们写出的结论，要进行一一的分析，保证思维的严密性，培养学生的逻辑思维能力。

4教学过程设计

4.1复习回顾：

方程（1）有两个不同实根 （2）有相等的实根 （3）没有实根

求的取值范围。

设计意图：回顾旧知，利用判别式来判断二次方程在实数范围内有无根的情况，为下一步讨论在给定区间（范围缩小）有根做铺垫。

4.2 创设情境、导入新课

问题1：若方程在区间上有两个不同的实根呢？

设计意图：在给定区间上有两个不同的实数根，只能用初中所学习的求根公式，把方程的两根用表示出来，限定在区间上，转化为求解不等式的问题。

问题2：有没有更好的处理方法？

设计意图：由于还没系统的学习解不等式，在解不等式组时会出现不好解的情况，激发学生研究该问题的兴趣。需要另辟蹊径，直接切入研究的课题----二次方程根的分布问题。

4.2.1 教师引导，建立数与形的关系，渗透直观想象素养

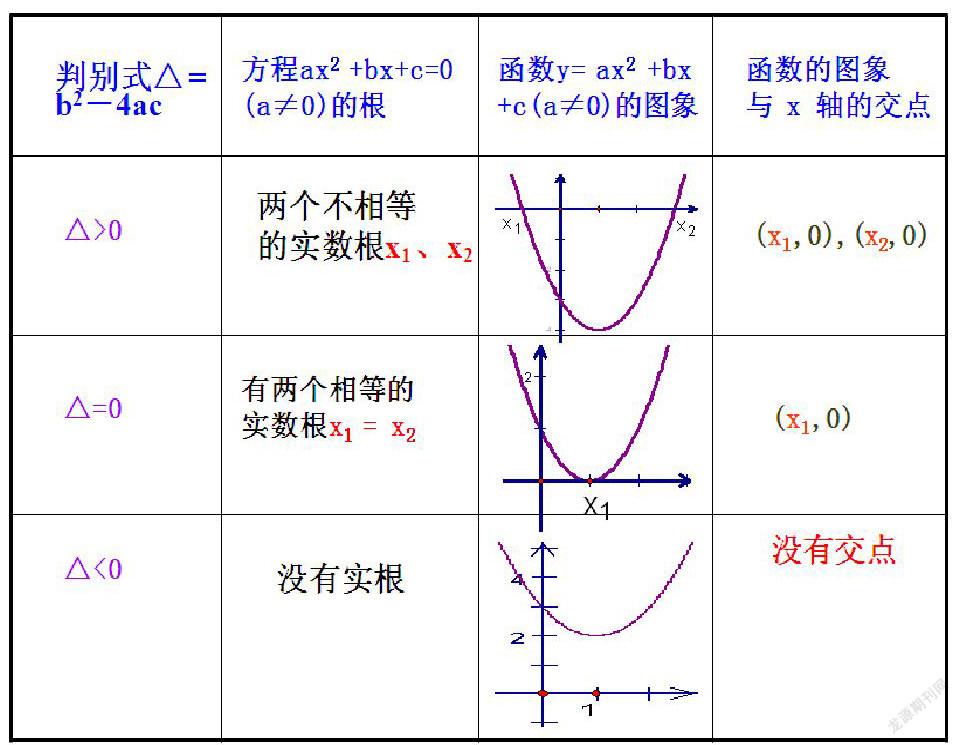
一元二次方程的根及相应的二次函数 的图象与 轴交点的有如下关系：

设计意图：已经学习过函数零点的相关内容，引导学生根据方程与函数的关系，利用数形结合思想，将二次方程根的分布问题转化为讨论函数零点的问题，培养直观想象能力。

问题1：方程的根等价于函数的零点，所以研究二次方程的根可以转化为研究二次函数的零点。此问题转化为，在区间上与轴有两个交点，那么如何保证二次函数与轴有两个交点呢，决定二次函数图象的因素有哪些呢？

设计意图：引导学生用函数零点研究方程根的分布，画出对应函数的图像，考虑影响二次函数图象的因素。开口方向，判别式，对称轴位置，与y轴交点。从形的角度解决问题，进一步培养直观想象能力。

其一：保证方程有根

问题2：我们发现开口向上且过定点，仅仅是不可以的，所以还要要求对称轴怎么样呢？

设计意图：引导学生画图解决问题，利用数形结合的思想，增加条件。其二：对称轴往区间中间移动。

问题3：对称轴限定在区间上，但是如何保证函数与轴的交点恰好落在区间上呢？

设计意图：提醒学生前面的两个条件是不够的，还需要加条件约束，即考虑区间端点函数值的符号。培养逻辑思维的严谨性。

整理思路，书写解题过程。

问题4：条件能够得到方程在区间上有两个不同的实根吗？

设计意图：引导学生积极思考，利用函数与方程的关系，从图形直观得到等价关系即列出的式子可以得到方程在区间上有两个不同的实根。

归纳总结，得到一般结论：

4.2.2 问题深究，巧用直观想象解决问题

问题5：若区间改为呢？再改为呢？

设计意图：将区间一个端点改为，让学生们思考能否用前面总结的规律去做，找到区别与联系。

例2.关于的方程的一根，另一根求的取值范围。

问题6：还需要来锁定有两个根吗？根据二次函数的特点及零点存在定理能否利用区间端点函数值的正负锁定？

设计意图：引导学生利用数形结合的思想，通过画出函数的大致图形，利用零点存在定理我们只需要通过区间端点函数值的正负就可以锁定，从而解出此题。

整理思路，书写解题过程。

问题7：条件能够得到方程两根分别落在区间上吗？

设计意图：引导学生积极思考，利用二次函数的特点及零点存在定理、端点函数值的正负就可以确定在题中所给定的两个区间。

归纳总结，得到一般结论：

设计意图：由特殊到一般，总结规律。

4.2.3 问题变式，落实直观想象素养

变式1.已知关于的方程的一根比小，另一根比1大，求实数的取值范围。

问题8：能否写出方程的根在哪个区间？变式1与例2的区别在哪里？

设计意图：通过对题目的分析，将文字语言转化为数学语言，明确此题是说方程的两根落在不同的区间，而区间的端点是，类比例2得出的一般结论来解出此题。

变式2.已知关于的方程的一根比1小，另一根比1大，求实数的取值范围。

设计意图：加深对两根不在同一区间的理解，明确做题方法，巩固知识。

4.3总结归纳，掌握规律，提升直观想象核心素养

问题1：讨论二次方程根的分布问题，我们需要考虑哪些因素？

问题2：本节讨论问题的数学思想方法是什么，核心素养有哪些？

设计意图：引导学生对所学的知识和数学思想方法的总结，并对学生的学习过程进行反思，为今后的学习进打下坚实的基础。

5.总结与反思

我国数学家华罗庚说： “数缺形时少直观，形少数时难入微;数形结合百般好，隔离分家万事休。”在数学的教与学中，数和形是两个重要的研究对象，它们联系密切。本节课通过问题设疑、创设问题情境，引导学生利用方程与函数思想，数形结合解决了二次方程根的分布问题，感受图形直观，培养直观想象核心素养。

参 考 文 献

[1] 人教A版《普道高中课程标准实验教科书-必修1》. [M]

[2] 指向学科核心素养的普通高中教学设计案例丛书.[ M] 杭州：浙江教育出版社.

[3] 冯祉璇，廖伟光，黄绍清，方強. 数形结合的思想在数学课堂教学中的实际应用. 《教师教学能力发展研究》总课题组科研成果集 （第十五卷）

[4] 石丽敏. 指向数学核心素养培养的高中例题教学研究. [D] 福州：福建师范大学.