深度揭示概念 感受负数价值
吴德娟 刘久成





【摘 要】负数来源于生活,同时具有构造特征。通过层层递进的三个板块,让学生在生活实例中感受负数表示相反意义的量,在数轴模型中感受负数在数轴上的排列、有理数的有序性以及数的分类,在运算推理中感受负数能进行更多的运算、解决更多的实际问题,从而获得对负数的本质认识,感受负数的价值,促进学生数学思维的发展。
【关键词】小学数学 认识负数 教学片段 教学评析
负数虽然在小学教学中所占篇幅较少,但对负数的教学研究还是受到了广泛关注。负数来源于生活,同时具有构造特征,为了让学生清晰地认识负数概念,了解负数的来龙去脉,深切感受负数的价值,我们进行了以下教学尝试。
教学片段1
师:同学们,在以前的學习中,我们认识了哪些数?
生:3、4、5、6等,这些是自然数。0.2、0.3、0.45等,这些是小数。
师:还有不同类的数吗?
生:1— 2、1— 4、3— 4等,这些都是分数。
师:是啊,我们认识了整数、小数和分数。在人类历史的长河中,人们曾用小石子、结绳和刻痕等来计数,随着生产发展、交流增多、语言不断丰富,于是逐渐产生了十进制计数法,并形成了现在的整数。人们在分物或测量的时候发现整数不够用了,于是产生了分数和小数。今天我们还要来认识一种新数。(板书课题:认识负数)
【评析】本课一开始教师就提出:我们已经认识了哪些数?帮助回忆旧知,并对已经认识的整数、分数、小数的产生进行了概述,渗透了数学史教育,让学生认识到数学不仅源于生活实践,也源于理性思考,为学生从不同侧面认识负数埋下了伏笔。
板块一:在生活实例中初识负数
教学片段2
师:认识了整数、分数和小数,为什么还要认识负数呢?让我们到生活中去寻找答案。如图1所示,甲、乙两组参加知识竞赛,第一题过后,甲组答对,乙组答错,两组现在的比分各是多少?
生1:甲组得了20分,就用20来表示,乙组答错,比0分还少20分,我认为用负20来表示。
师:-20会读吗?会写吗?表示什么意思?(板书:-20)
师:为什么乙组的得分不用以前学过的数表示?
生2:因为用以前的数表示比0分要高,而乙组比0分低。
生3:这个数比0小,要用负数来表示。
【评析】由于正负数的基本含义是具有相反意义的量,同时离不开“0”点的确定,而“0”点的确定带有人为规定的特点。为分步推进,这里改变了教材中通过温度计引入负数的做法,而是利用知识竞赛的得分、失分这一生活中非常熟悉的事例,首先让学生初步感受到正负数具有相反意义的特征。
教学片段3
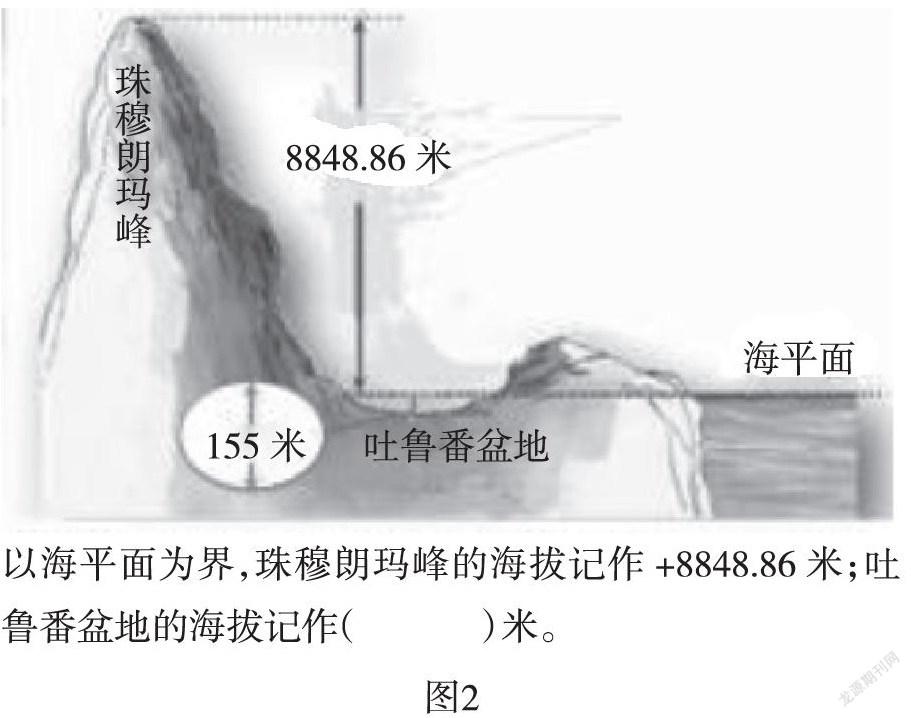
(出示海拔高度图,如图2)
师:吐鲁番盆地该怎么表示?想一想为什么你会选择用负数来表示。
生:我用-155来表示,因为吐鲁番盆地比海平面还要低,海平面是0米,比0还要少就用负数表示。
师:同学们在观察图的时候,以海平面为分界点,海平面以上的高度用+8848.86来表示,海平面以下的高度用-155表示。
师:像-20和-155这样的数都是负数,像20和+8848.86这样的数都是正数。正数可以加正号,也可以不加,正号可以省略。负号可以省略吗?
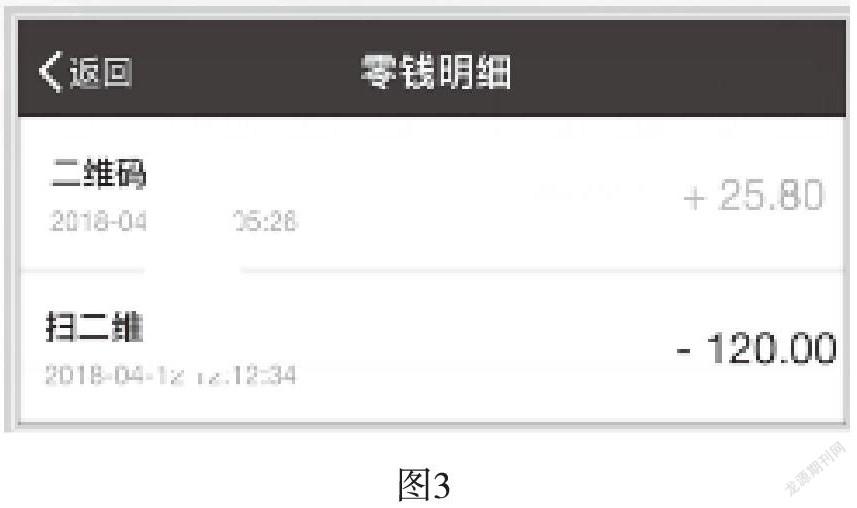
(出示微信账单,如图3)
师:下面是一份微信账单,你能读懂这两个数分别是什么意思吗?
生:+25.8元表示增加了的钱,-120元表示花去了120元。
师:这里的正数表示收入,那负数表示什么呢?
生:支出。
师:同学们能够根据生活实际理解这两个数的意思,支出的钱数可以用负数表示,收入的钱数可以用正数表示。
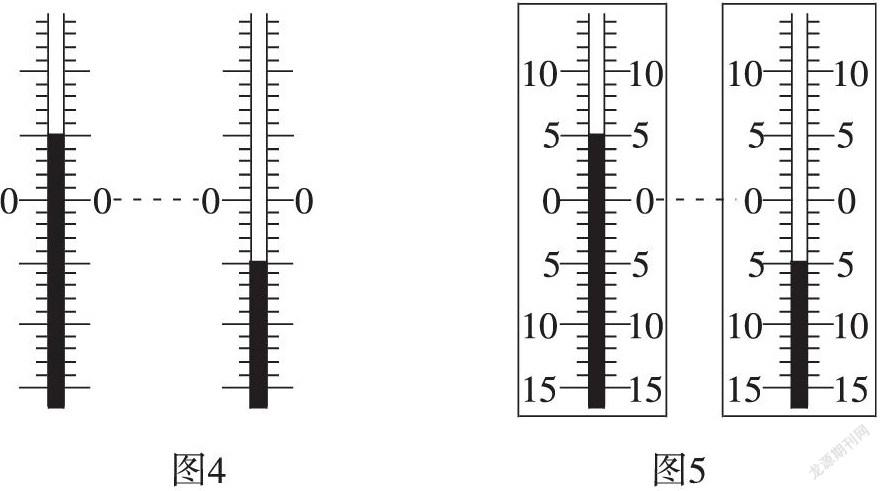
(出示温度计,如图4和图5)师:图4中这两个温度计的示数用正数还是负数来表示呢?
生:左边的图用正数表示,右边的图用负数表示。因为左边的温度比0摄氏度高,右边的温度比0摄氏度低。
师:现在能读出图5中两温度计显示的温度各是多少摄氏度吗?
(学生读并写出温度计上的温度)
师:刚才大家在判断用正数还是用负数表示的时候,首先需要确定什么?
生:先要确定0摄氏度在哪里。
师:0有什么作用?
生1:我认为0是把正数和负数隔开的。
生2:0是正数和负数中间的数。
生3:0的上面是正数,0的下面是负数。
生4:0在这儿是一个分界点,分界点的上面是正数,分界点的下面是负数。
师:大家说得都非常有道理,知道了0在表示正负数中的作用,它是正数和负数的分界点。
(板书:分界)
师:我们研究了4个问题,在每一幅图中,既有正数也有负数,对照每一组数表示的含义,比一比,你有什么发现?(对照图,见图6)
生1:我发现右边的都是正数,左边的都是负数,我想中间应该是0吧。
生2:我发现正数表示的意思和负数是相反的,比如20分是得分,-20分是扣分,得分和扣分是相反的。收入和支出也是相反的,上和下也是相反的。
生3:我同意你的看法,我也认为正数和负数的意义是相反的。
师:这几幅图中,都含有相反的情况,得分和扣分,海平面以上和以下,收入和支出,当遇到这样相反情况的时候,人们借用“-”号,创造了负数。有了负数,我们的表达会更加简洁、准确。
【评析】通过记分表、海拔、账单、温度计四个问题的讨论,从负数的自然意义(如记分表、账单)到人为规定意义(如海拔、温度计)的理解,让学生充分感受到,正数、负数是表示相反意义的量,同时认识到“0”的定位作用。温度计上的零上5摄氏度在左、零下5摄氏度在右,正好与板书设计的左右相反,这一设计不仅提醒了学生书写时的规范,也在细节处强化了学生对概念的认识。通过四个问题的讨论,最后概括出:当遇到相反的情况时,人们借用“-”号,创造了负数。学生在解决这四个问题的过程中体会到负数来源于生活实际,同时具有构造的特征。
板块二:在数轴模型中感受负数
教学片段4
师:这是我们熟悉的数轴(如图7),从0开始往右延伸,自然数都在上面,也可以找到分数和小数。大家想想负数在哪里?
生:从0开始向左延伸,负数应该在上面。(课件演示)
师:点A是多少,你怎么想的?(-1、-2、-3未标)
生1:点A表示-1,因为它在0的左边。
生2:我要补充,它是在0的左边,而且它和0相隔1格,所以是-1。
生3:我也认为是-1,因为在0的右边一格是1,所以0的左边一格就是-1。
师:大家说得很有道理,确实是用-1表示。观察一下-1和1这两个点,它们到0的距离相等吗?
生:相等。
师:我们称它们为一对相反的数。你能找出2、3、1.4这些数的相反数吗?
(学生在数轴上指出)
师:观察数轴你有什么发现,跟你的同桌说一说。
生1:我发现0的左边的数比右边的数多一个负号。
生2:如果把这条数轴沿中间的0对折,这些数会重叠在一起。
生3:我补充,点会重合在一起,数如果把负号去掉,也会重合在一起。
生4:他们的意思是,每一个正数和它相应的负数关于0点是对称的,可以沿0点折起来重合在一起。
生5:正数在0的右面,负数在0的左边。
师:同学们发现正数和它相应的负数关于0点是对称的,有一个正数就能找到一个相应的负数,那么数轴上的每个点都是这样的吗?
生:不是,0没有。
师: 0这个数很特殊,其实,它的相反数就是它自己。所以呢,0既不是正数也不是负数,它是正数和负数的分界。
师:如果把数轴上的数分为正数和负数两类,大家同意吗?如果不同意,那怎么改?
生:应该分为三类——正数、负数和0,因为0既不是正数也不是负数。
【评析】在数轴上讨论负数比起生活中的负数要抽象一些,但它能整体地反映负数的特征,负数与正数的关系,强化了0的特殊性,以及0在认识正数、负数中的作用。
教学片段5
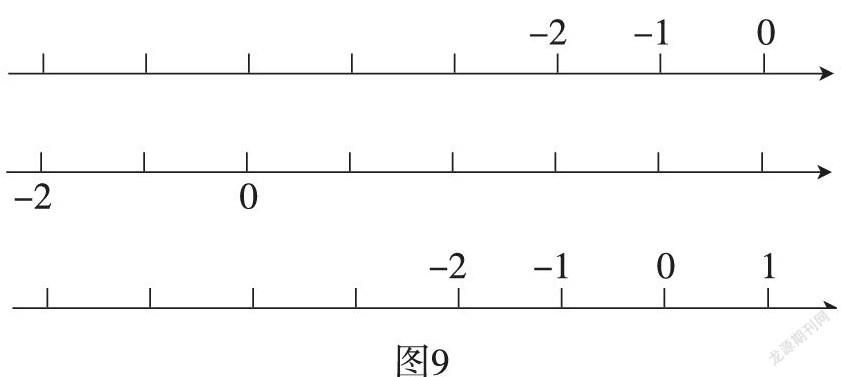
师:请同学们完成下面这道练习,在图8中标一标。
(展示学生完成的练习结果,如图9)
师:为什么同学们表示出的-2的位置不一样呢?
生:因为0点的位置不一样,所以-2的位置也不一样。
师:虽然大家标的-2的位置不一样,观察三个学生的标法,有没有什么共同点呢?
生:-2都在0左边2格,也就是说如果确定了0的位置,那么它的左边2格就是-2的位置了。
师:当我们要表示负数时,首先要确定0的位置,0的位置变化了,-2的位置也会变化。
【评析】出示数轴,并紧扣问题:负数在哪里?负数有多少?谁与谁是相反数?你有什么发现?展开讨论,环环相扣,各个击破。在数轴上认识负数,不仅形象直观,渗透数形结合思想,而且有利于学生感受有理数的有序性。由此,学生不难发现规律:每一个正数都有相对应的负数;正数都比负数大;数轴上越往左的数越小,越往右的数越大;等等。
为了凸显“0”的作用,教者特意安排了在数轴上标“-2”的练习,通过三种标法的对比,提问:同样是表示“-2”,为什么点的位置不同?从而强调了“0”的定位作用,这就抓住了数轴上表示负数的关键。
板块三:在运算推理中体会负数的应用
教学片段6
师:其实每一种数的产生,它的价值不仅是为了解决生活中的问题,数学科学的发展,同样有需要。以熟悉的1和2为例,组成不同的算式,请用数来表示计算的结果。
1+2= 1×2= 1÷2= 1-2=
师:1÷2能用整数表示吗?为什么?
生:1÷2不能用整数表示,因为不够1个了,用1— 2表示。
师:在除法运算中,不能整除时,我们可以用分数或小数来表示。
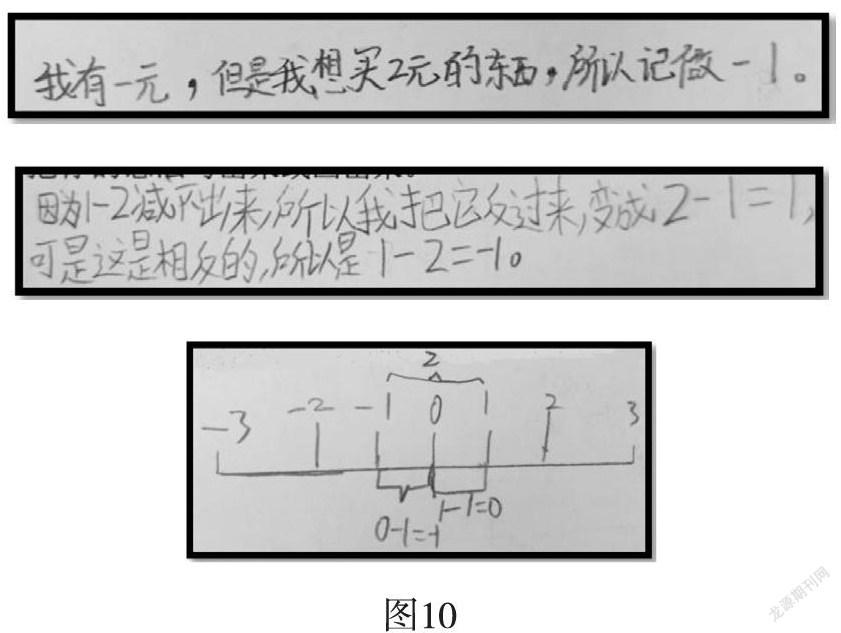
师:1-2的结果呢?你能写一写、画一画,让大家了解你的想法吗?
(学生独立活动,展示学生作品如图10,学生交流)
师:为什么计算1-2的时候你们想到了用负数来表示结果呢?
生:因为被减数减减数的时候不够减了,所以我们想到用负数来表示。
师(小结):人们在遇到小的数除以大的数,不够除了的情况后,创造了分数;人们在遇到小的数减大的数,不好减了的情况后,创造了负数。
【评析】数的一个重要功能是能够运算,新数的出现,常常受到运算的推动,比如“分数”的产生,原因之一就是基于整数除法运算的需要。这里教者利用一组算式,放手让学生思考:1-2=?写出你的想法,再进行全班交流。学生从运算角度体会引进负数的必要,以及负数在运算中表达的合理性,同时也为后续学习负数的四则运算、解方程等知识做铺垫。
总评
认识负数是小学生数概念的又一次重要扩展。以前小学生学习的都是“算术数”,这些数与生活实际联系紧密,学生感受和理解这些数的含义相对比较容易。学生虽然在日常生活中了解过负数,但在学生生活中直接应用负数的情况并不多见。因此,学生真正理解负数的概念还是存在一定困难的。为此,教者在深入研究教材的基础上,对教学过程做了精心设计,体现了以下特色:
(1)改變单纯由温度计引入负数的做法,采用丰富多样的事例,循序渐进地揭示负数是表示相反意义的量。“相反意义的量”通常有自然意义和人为规定意义两种。输与赢、收与支、盈与亏等都是自然意义下“相反意义的量”,学生易于理解;而温度、海拔等都需要规定“0”点,具有“人造”的特点,相对复杂。因此,教者改由温度计引入负数为从比赛的得分、扣分出发,让学生初步感受具有相反意义的量是合适的。
(2)注重概括提炼,揭示负数概念的本质。概念是数学知识的细胞,是构成数学公式、规则、命题等规律性知识的基础。学习数学概念,要让学生尽可能了解概念从何而来,它的本质是什么,我们应该如何理解。教者通过生活中的负数、数轴上的负数、运算中的负数,层层递进,逐步抽象,及时概括,不断丰富负数的内涵,让学生不仅认识到负数是具有相反意义的量,同时由于“0”的作用讨论,让负数的意义更加完整,负数与正数的关系更加清晰,通过对数的分类让学生能更加清楚地认识到负数是一种新数。
(3)三个板块步步深入,让学生充分感受到负数来自多方面的需要,体验到负数的价值。具体说来:
通过第一个板块的学习,让学生感受到负数是表示相反意义的量,运用负数能让生活中问题的表达更加准确。
通过第二个板块的学习,让学生感受到负数在数轴上的排列、有理数的有序性,以及数的分类,让学生对数的认识更加全面。
通过第三个板块的学习,让学生感受到有了负数能进行更多的运算,有利于解决更多的实际问题,也促进了数学科学的发展。
总之,本课创造性地运用教材,别具一格地对各个环节进行了精心设计,通过三个板块的有序推进,让学生对负数的本质及其规律有了清晰的认识,促进了学生数学思维的发展。

