与积分有关的一个极限及其应用

黄永忠， 吴 洁

(华中科技大学 >数学与统计学院，武汉430074)

1 引 言

与定积分有关的极限问题常常涉及综合知识，有一定难度但同时也有一些好的结论，见文[1-8]. 文[9]综合习题第62题：

这个结论的证明较容易，基本思路是用“拟合法”(见命题1的证明). 文[9]的接下来63题就是这个结果的应用题(见例4)，其实第6题也是这个结论的应用题(见例1).

2 对应数列极限及其应用

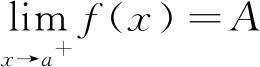
|f(x)-A|<ε.

注意到

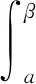
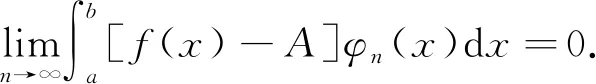
随后几个命题可作相应说明，不再提及.

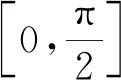
证利用Beta函数和Gamma函数，得

(1)

其中等价关系由下列Stirling公式而得

注2 利用本例，特别是式(1)， 可立即简洁地得到文[10]第1.46题的极限(其中f，g是连续函数).

因为

即φn(x)在[c，b]上一致收敛于零， 所以由命题1后注1得

下例来自文[10]， 那里用Lebesgue控制收敛定理，这里用命题1.

∀c∈(0，1)，φn(x)在[c，1]上满足

对偶地，有如下结论：

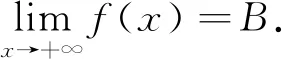
例4[9]设函数f(x)在积分区间上连续，求下列极限：

解因为xn在右端点1的任何区间上不一致收敛，所以(1)与f(1)有关. 余下题可类似把握.

(i) 设φn(x)=(n+1)xn，则它满足命题1′对φn(x)的条件，从而得到

(ii) 令t=x2，利用Beta函数得

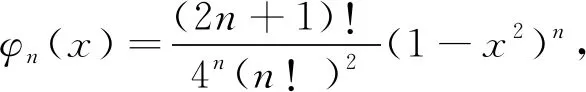
也就是φn(x)在[0，c]上一致收敛于零. 因此，由命题1，有

下面例5来自文[10]第1.45题，做法与文[10]不同， 那里用到有界收敛定理，这在通常的数学分析或微积分教材中并不提及.

解设m，M为正常数，且m≤f(x)≤M(x∈[0，1])，则

从而由迫敛性定理得到

所求极限为1∞型. 于是利用等价关系ln(1+y)～y(y→0)知，求极限J归结为求极限

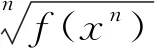
|lnf(xn)|≤C，x∈[0，1].

由不等式

得到

于是

因此，令t=xn，有

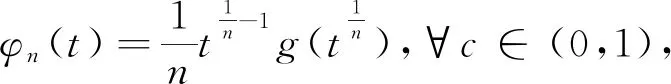
也就是φn(t)在[c，1]上一致收敛于零，其中常数β使0≤g(x)≤β(x∈[0，1]). 因此由命题1得L=lnf(0)，从而得所求极限J=f(0).

3 对应函数极限及其应用

定义设Uo(x0，δ′)为实数x0的一个去心邻域，I⊆R是一个区间. 对定义在平面区域Uo(x0，δ′)×I上的函数w(x，y)，称w(x，y)当x→x0时关于y在I上一致收敛于零，是指∀ε>0，存在δ>0(δ≤δ′)，当0<|x-x0|<δ时，∀y∈I有|w(x，y)|<ε.

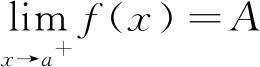
|f(x)-A|<ε.

注意到

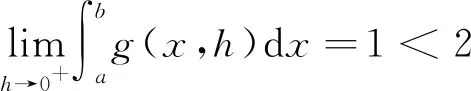
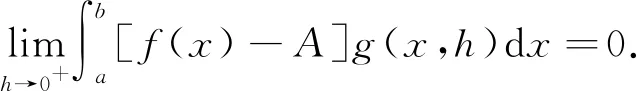
这里没有用函数的上极限. 命题1的证明后段也可以如这里的处理，用极限的定义.

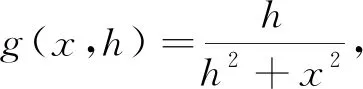
为方便应用，下面给出命题3和命题4，其证明与命题2雷同，从略.

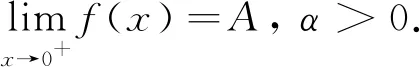
解令μ(x，t)=xαt-(1+α)，则

注4 若f(x)在[0，1]上连续，则本题可用洛必达法则来做.

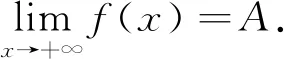
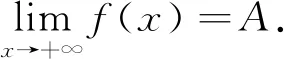
4 结 论

本文对文[9]的一道综合习题进行推广，得到相应数列极限和函数极限的计算式子，其中的积分可以是变限的也可以是瑕积分、无穷积分等，并通过较多的例子展现了这种推广的全面性和有效性.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.