基于支持向量回归机的机器人定位精度提高

于连栋，常雅琪，赵会宁*，曹家铭，姜一舟

（1. 合肥工业大学 仪器科学与光电工程学院，安徽 合肥230009；2. 测量理论与精密仪器安徽省重点实验室，安徽 合肥230009）

1 引 言

随着机器人技术的快速发展，工业机器人广泛应用于自动化、先进制造等领域。机器人具有较好的重复定位精度，但绝对定位精度较差，使其适用范围受到了严重的限制。因此，如何进一步提高机器人的绝对定位精度成为研究的焦点。目前，解决上述问题主要有两种方式：提高机器人的加工和装配精度，以增加开发成本为代价，更新速度较慢，难以满足生产需要；采用数学方法修正结构参数与非结构参数的误差，在不增加任何成本情况下，能够有效地提高机器人的绝对定位精度。

机器人结构参数标定通常包括建模、测量、参数辨识和补偿4 个步骤。 1995 年Denavit 和Hartenberg 提出D-H 建模，并被广泛应用于机器人建模［1］。Samad 等提出5 参数MD-H 模型［2］，改进了D-H 模型相邻两个关节平行时产生奇异的问题。在测量方面，激光跟踪仪［3］、视觉跟踪系统［4］和球杆仪［5］等能够实现高精度测量，为误差修正提供标准量。 在参数识别方面，最小二乘法［6］具有原理简单和计算量大的特点，LM 算法［7］、扩展卡尔曼滤波［8］等是经典的解决方法。然而，基于机器人运动学的建模仅能部分修正机器人的制造和装配误差，因此，结构参数误差的占比不同，补偿效果在整个空间不均匀，修正效果受到限制。

非结构参数误差主要受杆件变形、温度等方面的影响。Lubrano 等［9］通过在机器人上布置温度传感器测量其自身温度，实现了温度补偿。Gong 等［10］研究了连杆柔性以及温度对机器人的影响，连杆温度的升高造成零件的膨胀，重力与载荷使连杆变形，难以直接消除。Nguyen 等［11］通过将参数辨识后的残差作为ANN 模型的输出，关节转角作为输入，建立了机器人非结构参数误差修正模型。部分学者通过将结构参数与非结构参数误差当做整体，统一考虑，为机器人标定提供了新的思路。Zeng 等［12］对机器人误差进行分析，提出了基于误差相似性的精度补偿方法。Guanbin 等［13］采用BP 神经网 络与粒 子群算法混合，搜索最优变量，以补偿运动学参数的误差。赵俊伟等［14］采用空间差值法，自动调用之前库内补偿值进行补偿。

相对于上述方法，支持向量回归机（Support Vector Regression，SVR）整体考虑结构与非结构参数误差，将低维非线性自变量空间，转至高维特征空间，使其实现可线性规划的学习系统。同时，引入损失参数减小随机误差对预测模型的影响，能够通过较少的训练样本获得较强的泛化能力，不易陷入局部最优，结构更简单，学习效果更好［15-16］。

机器人的杆件变形、温度变形等因素引起的非结构参数误差会随着机器人在工作空间的运动，产生一定规律的变化。网格划分便成为解决这类问题的有效途径，王一等［17］提出了扇形网格划分方法，周炜等［18］采用网格划分的方法实现了机器人结构参数与非结构参数的误差修正。

本文采用Universal robot 公司的UR5 机器人作为研究对象，采用MDH 模型为基础，通过对工作空间进行网格划分，并利用SVR 方法建立机器人转角与机器人误差之间的关系模型，以实现网格内绝对定位误差的补偿。

2 机器人运动模型

机器人运动学建模的经典方法是D-H 模型［1］，根据D-H 模型的描述，关节之间的转换可以用4 个结构参数进行描述。这4 个结构参数是连杆长度a，连杆偏距d，连杆绕X 轴旋转转角α，以及关节转角θ。

采用如图1 所示的UR5 机器人作为研究对象，共有6 个转动关节，其中有两相邻关节旋转轴系处于平行状态，D-H 模型存在着病态性。为了克服这类问题，MDH 模型在D-H 模型的基础上增加了绕Y 轴的转动量β。在相邻关节不平行时，β=0，仅当两相邻关节平行时存在β。如图2所示，采用MDH 模型可以获得机器人相邻连杆的坐标转换关系，以确定最末端坐标值。连杆之间的转换关系为：

图1 UR5 机器人关节坐标系示意图Fig. 1 Schematic diagram of UR5 robot coordinate system

图2 MDH 模型连杆坐标系Fig. 2 Linkage coordinate system of MDH model

对于n自由度转动机器人，末端位姿是各个连杆变换矩阵的乘积。机器人运动学模型为：

机器人末端工具的实际位置P=[Px Py Pz]T。由于各参数的理论值与实际值存在一定的偏差，所以机器人末端位置的实际值与理论值也不同，存在定位误差e=P-P′，其单点绝对定位误差在笛卡尔坐标系中存在3 个方向的距离误差ei∈R3。

3 支持向量回归机理论

假 设 一 个 样 本 集{(x1，y1)，(x2，y2)，…，x}(xm，ym) ，其中xi∈Rn作为样本集自变量，yi∈R表示样本集因变量。 使用非线性映射将数据{x1，x2，…，xm}映射到高维空间F，再在高维空间进行线性拟合。因此可以将函数关系式用公式（3）表达：

式中：w是将样本数据映射到高维空间之后对应的权重向量，b被称为偏置项。

在利用SVR 进行计算时，会引入参数ε的不敏感损失函数度量，如式（4）所示。若回归函数误差小于损失参数ε，忽略对回归结果的影响，尽可能包含更多数据点。

根据样本估计出回归函数f(x)，使得yi与f(x)的差值都很小，将问题转化为：

式（5）作为目标函数。考虑到部分样本不能被正确分类，引入松弛因子ξi，ξi*≥0，惩罚因子C＞0，表示大于ε的样本惩罚程度。式（5）是一个二次规划问题，只要优化求解方法满足KKT条件，通常采用Lagrange 对偶问题解决方法，以及Lagrange 乘数法。引入拉格朗日乘子αi和α*i，将目标函数转化为：

式中K(xi，xj) 为核函数。通过选择合适的核函数，不仅能提高预测模型的精度，而且能降低随机噪声对预测模型的影响和运算量。目前，常用的核函数及其特点如下：多项式函数，维数过高时其计算复杂度增加；线性函数，适用于输入输出维度相同的训练模型；sigmoid 函数，类似于多层神经网络的结构，具有一定的局限性；径向基函数（Radial Basis Function，RBF），对样本要求低、应用广泛、灵活性高。由于机器人输入输出维度不同以及模型复杂度高，选择RBF 进行训练，具体表达式为：

通过指数关系，将输入样本空间映射到无限维空间，从而实现高精度非线性拟合。

4 机器人单点标定误差模型

具有旋转关节的n-DOF（Degree of Freedom）机器人采样样本m个，建立样本集{(θ1，e1)，(θ2，e2)，…，(θm，em) }T，θ∈Rn，为机器人n个转角数值，ei为对应在直角坐标系中的误差值。具有n旋转关节的机器人的末端位置误差可以表示为：ei=E(θ)=ωi，1θi，1+ωi，2θi，2+ …+ωi，nθi，n，（10）式中：ei= [exi eyi ezi]T，是机器人x，y，z3 个方向的误差向量；ωij= [ωxij ωyij ωzij]T，表示结构参数和非结构参数有关的转角补偿系数。误差补偿函数E(θ)是关节转角与末端坐标误差的函数表达式。

图3 坐标转换示意图Fig. 3 Coordinate conversion relationship

如图3 所示，利用激光跟踪仪测量机器人末端坐标的笛卡尔坐标值PMT，在理想结构参数与运动学模型获得机器人的理论末端坐标值PST。采用RANSAC 快速转换算法获得坐标转换矩阵PSM［19］。单点位置误差表示为：

在采用式（12）进行预测时，需要对平衡系数c，允许误差ε，以及高斯核函数σ进行选择。随着c的增加，训练时间变长，训练样本集的标准均方差成反比例函数减小。高斯核函数σ越小，标准均方差越小。随着允许误差的减小，被考虑的样本减少，标准均方差增大。综合考虑，最终选定平衡系数c=100，允许误差ε=0. 2，高斯核函数σ=2。

5 空间网格划分

为提高SVR 模型的训练精度，降低非结构参数的影响，需要对机器人工作空间进行划分。网格划分的好坏会直接影响机器人标定的精度与速度。如图4 所示，网格划分按照机器人末端位置区域进行形状大小的分类。网格的大小与标定结果在一定范围内成反比，网格越小，给实际操作带来了很大的难度；网格越大，标定结果越差。

图4 机器人工作空间网格划分Fig. 4 Grid division of robot workspace

网格划分步骤如下：

（1）定义网格属性，包括形状和大小。若采用扇形网格划分方法，结合机器人3 个基础转角进行划分，该方法比较贴合机器人的移动方式。但求解预测误差是在笛卡尔坐标系中，导致标定效果并不理想。针对上述情况，本文采用如图4所示的立方体结构，便于最终的误差修正，且标定效果较好。立方体大小的选择主要根据所需精度予以决策。根据洪鹏等对网格大小选取的分析［20］，本文采用100 mm×100 mm×100 mm 的正立方体结构对UR5 机器人进行网格划分。

图5 训练样本量与标定精度之间的关系Fig. 5 Relationship between training sample size and accuracy

（2）划分网格，获取采样点集。机器人工作空间是一个球形，网格划分采用立方体结构，无法覆盖所有空间，对于边界空间，尽量减小网格大小，以实现准确修正。在单一网格内，采样点数量对最终训练结果的影响结果如图5 所示。标准偏差在0～10 个采样区间快速下降，并在10～30 个采样区间出现拐点，对误差的修正效果趋于平稳。在保证训练结果的前提下，采用较少的训练样本可以减小采样难度，也避免发生过拟合。因此，选择20 个点为单一网格的采样数目。

6 实验结果及分析

如图6 所示，采用U R 5 机器人作为研究对象，并利用A P I T racker T 3 激光跟踪仪作为测量仪器，其测角精度为± 3. 5 μm /m，测长精度为±0. 5 μm/m。 UR5 机器人的关节转角Θ=[θ1，θ2，…，θm]T，θ∈R6，作 为 自 变 量 输 入 模 型 。因变量分别为机器人末端x，y，z3 个方向的误差值。

图6 UR5 机器人与激光跟踪仪实验装置Fig. 6 UR5 robot and laser tracker experimental setup

如图7 所示，机器人臂长的20%～80% 区域作为中心位置，80%～100% 区域作为边缘位置，划分边长为100 mm 的正立方体，每个网格内随机运动采样120 个点，其中20 个点作为训练样本。按照第4 节所述方法，获得误差值作为模型的因变量，对SVR 模型训练，以确定式（8）中的参数α，α*和b。 不同位置的预测结果如图8 所示，x，y，z3 个方向的原始位置误差和预测模型结果基本重合，并计算两者相关系数的均值为0. 944，均趋近于1，表明训练效果较好。

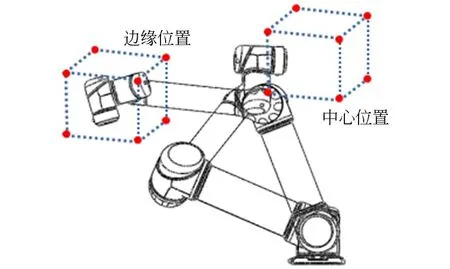
图7 UR5 机器人采样位置选择Fig. 7 Selection of UR5 robot sampling position

其余100 个采样点作为验证，评价SVR 的系数拟合结果。采用验证样本进行验证，并随机抽取50 个点进行观察，得到如图9 所示的验证结果。由图9 可知，不同位置的验证结果和原始误差的重合度较好。

为了验证已提出方法的优势，与LM 算法进行比较，结果如表1 所示。图10 为不同位置修正前后绝对距离误差示意图。结果表明，机器人末端位置不同，会造成原始误差分布不同，但定位精度均有明显提高，且效果优于LM 算法。

图8 不同位置的训练结果Fig. 8 Training results at different positions

图9 不同位置的验证结果Fig. 9 Verification results at different positions

图10 不同方法的绝对定位精度对比Fig. 10 Comparison of absolute accuracy between different methods

表1 不同方法的补偿效果Tab. 1 Compensation effects of methods at different positions （mm）

7 结 论

结构参数误差和非结构参数误差是影响机器人末端单点定位精度的重要因素。本文采用SVR，同步考量结构参数误差与非结构参数误差。通过机器人转角与末端绝对定位误差的高维拟合，建立两者之间的直接联系，实现了位置误差的预测与修正。实验结果表明，将机器人中心位置与边缘位置分别从2. 107 mm 和2. 182 mm，修正到0. 103 mm 和0. 123 mm，有效地提高了机器人的绝对定位精度。