氧化硅光波导侧壁角测量精度的提高

尚鸿鹏，孙德贵，3*，李天成，于 汀，曾春红，2，姜会林*

（1. 长春理工大学 理学院 光电工程学院，吉林 长春130022；2. 中国科学院 苏州纳米所，江苏 苏州215125；3. 渥太华大学 光子学中心，加拿大 渥太华ONK1N6N5）

1 引 言

硅基氧化硅（SiO2）光波导是构成光网络中无源光器件的重要组成部分［1-2］。随着通信领域的飞速发展，信息量的需求急剧增长，光通信器件加工工艺技术不断更新，新的波导加工工艺不断涌现。作为无源光器件的核心，SiO2波导仍起着不可替代的作用。 依靠平面光波线路器件（Planar Lightwave Circuit，PLC）工 艺 制 造 的SiO2波导具有光传输损耗小，对传输光波长不敏感，与传统的半导体加工工艺相兼容，与单模光纤耦合效率高等优点而广泛应用在通信领域［3-4］。SiO2波导制备的光通信器件，如光分束器（Splitter）、可调光衰减器（Variable Optical Attenuator，VOA）、光开关（Optical Switch，OS）等的性能则直接关系到整体光网络的工作状态［5-6］。

平面光波线路器件的加工通常采用刻蚀工艺。刻蚀工艺存在固有缺陷，在光刻、掩膜质量、刻蚀条件等均会导致器件的波导存在形貌误差，从而增加波导光在传输过程中的散射损耗［7］。波导刻蚀以后波导侧壁与基底存在侧壁角度，增加了偏振相关损耗，限制了器件在通信设备中的性能［8］。

目前，常见的芯层精确测量装置包括原子力显微镜（Atomic Force Microscope，AFM）、扫描电 子 显 微 镜（Scanning Electron Microscope，SEM）和激光共聚焦显微镜（Confocal Laser Scanning Microscope，CLSM）等［9-11］。 其 中 ，CLSM 具有非接触，实现无损检测完整晶片等优点，SiO2波导器件由于芯层和包层的折射率差很小（0. 1%～0. 75%），无法使用CLSM 对波导芯层侧壁角进行测量［12］。另外，芯层和包层均为绝缘材料无法使用SEM 对端面芯层的侧壁角度进行精确检测［13］。

在SiO2波导加工工艺中，波导芯层与包层间折射率差很小，导致上包层沉积完成后很难通过检测仪器对芯层的形貌进行检测，无法进行刻蚀形貌表征和侧壁角度测量，这是SiO2波导的理论设计与实际加工工艺间的矛盾所在［14］。因此，对于器件波导通道的形貌表征，无论从理论还是技术上进行深入研究是十分必要的［15］。

本文提出了一种应用光学图像显微镜（Optical Image Microscope，OIM）测量沉积包层后波导通道侧壁角度的测量方法［13］。通过应用光学显微镜测量微米级波导通道，对测量采集的图像数据的精度和误差进行了修正，达到了对波导侧壁角度进行精确测量的目的。

2 测量实验及原理

实验样片SiO2波导以Si 为基底材料，通过（Plasma Enhanced Chemical Vapor Deposition，PECVD）工艺沉积8 μ m 底包层后在其表面沉积6 μ m 的SiO2作为波导芯层主材料，再经过蒸镀金属掩膜、光刻、刻蚀掩膜、去除光刻胶、刻蚀芯层以及沉积12 μ m 上包层等主要工艺完成器件制造，芯层与包层的折射率差为0. 75%，通过DISCO 划片机对完整晶片中的器件进行划片，并应用Krell-Flex 波导研磨机研磨波导端面。 图1（a）为完成沉积包层后的波导侧视图。 芯层端面结构设计为6 μ m×6 μ m 的 矩 形 。 但 由 于 刻 蚀 工 艺 的 不 稳定，实际波导通道不规则，存在侧壁角，其结构如图1（b）所示。在划片、端面研磨过程中难以保证波导z方向对应x，y方向均垂直，划片和研磨工艺导致x方向的倾角误差较大，所以波导立于光学显微镜载物台，波导上下端均存在倾角，如图1（c）所示。

图1 波导结构与测试放置示意图Fig. 1 Schematic diagram of waveguide chip

图1 （b）中，φ1和φ2分别表示波导芯层左端和右端侧壁角度的余角，wt和wb分别表示波导的顶边和底边的宽度，h为波导高度。图1（c）中，θ1和θ2分别为波导上端和下端相对物镜平面的倾角，波导相对物镜平面的总倾角为θt=θ1+θ2。波导底边与顶边的长度差为：

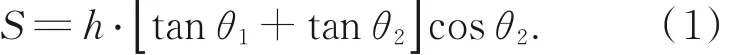
由式（1）分析得出，当测量过程中存在S时波导的顶边和底边不能处于同一物方焦平面，观测时端面成像呈现梯形。

2.1 显微镜物镜和目镜之间图像倍增关系

光学显微镜光路如图2 所示。光路主要由物镜部分L1和目镜部分L2组成，焦点分别表示F1和F2，光学间距（Optical Tube Length，OTL）［16］，焦距为f1和f2，L为虚像到目镜焦平面的距离［17］。

用u1和v1分别表示物镜的物距和像距，放大倍数为M1=v1/u1，可得到像距和目镜L2的关系为：

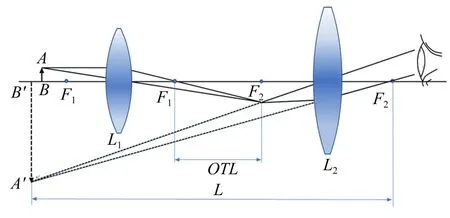
图2 BMM-50 型显微镜成像系统示意图Fig. 2 Schematic of imaging system of optical microscope-BMM-50

通过光学成像显微镜总放大倍数自校准方法［18］，有效放大倍数可以表示为：

其中k为镜筒系数，通常为1. 0。

2.2 波导侧壁角度与显微物镜放大倍数

波导器件立于载物台上，且波导顶边与显微物镜处于同一焦平面，此时显微物镜的放大倍数为M。显微镜采集到的波导端形貌为实际尺寸，即H=M·h，Wt=M·wt，Wb=M·wb。

当器件与载物台之间存在角度θ2时，显微镜获得的波导投影高度为：

如果波导端面相对载物台的倾角为θt，高度为h，顶边宽度为wt，底边宽度为wb，在不同的放大倍数M，Mt，Mb下可以表示为：

在波导端面的显微测量过程中，可以将波导顶边或底边作为成像的物平面，由于器件端面相对于物镜存在倾角，成像过程中存在S的偏移，因此可以通过两种方式进行检测。首先将波导底边处于物镜物平面，此时顶边波导的实际宽度为wt，但是底边宽度wb因为偏离焦平面并非实际的宽度，对应的S偏移由倾角θt决定。此时，未处于焦平面的底边宽度由定义的物距变化表示为：

所以，显微镜的放大倍数不再是原显微镜的放大倍数，具体的放大倍数需要对焦平面为波导顶边和底边两种条件进行分析后确定。

2.2.1 波导底边处于物镜物平面

设定波导底边处于显微物镜焦平面，在不失一般性条件下，将波导底边分为Lb和Rb两部分，与显微镜成像系统的轴线正交，如图3 所示，即：

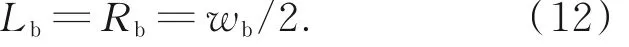
显微镜物镜光轴与波导底边处同一焦平面。

图3 显微镜观察时将波导底边成像分为对称的两部分Fig. 3 Separating and setting bottom line of waveguide end for two symmetric imaging parts of optical microscope

当波导边宽度固定时，波导顶边的宽度表示为：

实验中可通过显微镜测量得出波导底边宽度：

设定φ1m(A)和φ2m(A)分别表示波导端面显微成像的左右两端的侧壁角度，由式（15）和式（16）可得出显微镜图像后侧壁角度变化的表达式：

将式（7）和式（13）代入上式中可得出显微成像中两端侧壁角度和波导倾斜角度中间的关系：

通过式（19）和式（20）可以得出波导两侧壁角的变化为：

2.2.2 波导顶边处于物镜焦平面

当波导顶边处于物镜焦平面时，顶边的实际放大倍数无变化，底边放大倍数发生变化，于是将图3 所示的芯片顶边波导宽度设为Lt和Rt与物镜光轴垂直，即为Lt=Rt=wt/2。

相对底边宽度变化为：

显微成像后波导两侧壁倾角分别由φ1m(B)和φ2m(B)表示，并通过式（22）和式（23）可以得出显微成像的侧壁倾角改变，分别为：

于是可以得出波导侧壁倾角的变化为：

3 波导侧壁角度变化与倾角依赖关系

根据显微镜对波导芯片上下两个端面的波导底边或顶边聚焦的两种方式，通过上述数学模型进一步计算分析显微成像与波导侧壁角度的变化关系。直立波导倾角θ1和θ2的典型值设定为1. 0°，3. 0°和5. 0°，显微镜倍数设定为600×，对侧壁角度变化设定两种分析方法：（1）物镜对波导端面未聚焦并逐渐接近被检测端面；（2）物镜对波导端面未聚焦并远离被检测端面。通过计算发现，显微成像与波导侧壁角度的变化关系不依赖于聚焦点选择在波导端面的底边和顶边上，所以在下面的计算分析中只选择底边条件。

3.1 物镜逐渐接近波导端面过程分析

实验使用的光学成像显微镜型号为BMM-50，物镜的放大倍数M1=60，目镜放大倍数M2=10，通过总放大倍数自校准方法［17］的有效放大倍数M= 601，物镜的有效焦距f1=2. 9 mm，OTL=160. 0 mm。通过式（1）～式（5）得到物镜和目镜的其他基本参数：v1=176. 9 mm，u1=2. 9 mm，f2=140. 0 mm，v2=1 260. 0 mm，u2=126. 0 mm。首先将波导的顶边作为检测点，显微物镜焦平面由远到近逐渐接近波导端面，该过程中由于无法聚焦，显微成像质量较差，即θ1和θ2均会影响到显微镜的成像质量。根据图4（a）所示的检测原理可以测得非600×放大倍数下波导侧壁角度φ1m和φ2m的显微图像与实际波导侧壁角度φ1和φ2之间的变化关系。图4（b）所示为θ1和θ2倾斜角不同时3 个数值的变化规律。由此可知：通过数值模拟结果得出显微镜成像过程中侧壁倾角的变化与焦平面的选择无关。

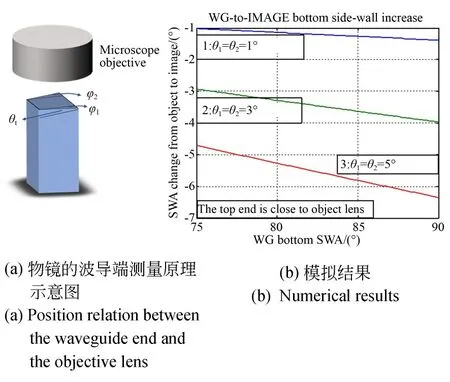
图4 物镜焦平面逐渐接近波导端面时波导倾角θ1 和θ2与成像侧壁角度之间的变化关系Fig. 4 Numerical calculations on side-wall angle changes of waveguide end from real device to microscope image for top-side of waveguide end approaching to objective lens with respect to θ1 and θ2 values

图4 是对于θ1和θ2波导端从实际设备到显微镜图像的侧壁角度变化的数值计算结果。为改进聚焦状态，使用可调器件倾角卡具使底端倾斜角θ2= 0°。当只有θ1影响显微镜的成像过程时，获得的波导φ1m（或φ2m）的显微镜图像和实际波导φ1（或φ2）显微镜图像随侧壁角度变化的数值计算结果比图4 中的结果缩小一倍。

3.2 物镜逐渐远离波导端面过程分析

物镜对波导端面未聚焦并远离被检测端面情况如图5（a）所示。图5（b）所示为波导φ1（或φ2）的显微镜图像与实际波导之间的侧壁角度变化关系的数值模拟结果。为得到更好的聚焦状态，使用可调器件倾角卡具消除底端倾斜角的影响，即θ2= 0°，此时，显微镜图像随侧壁角度变化的数值计算结果应该比图5 中的结果缩小一倍。

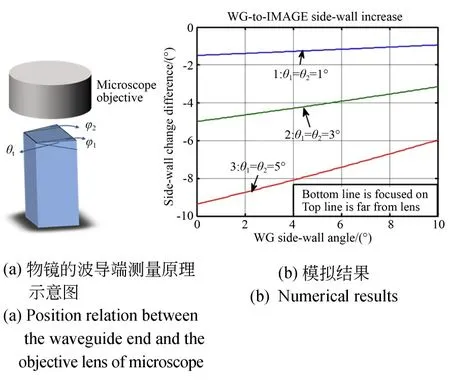
图5 物镜焦平面逐渐远离波导端面时，波导倾角θ1 和θ2与成像侧壁角度之间的变化关系Fig. 5 Numerical calculations on side-wall angle changes of waveguide end from real device to microscope image for top-side of waveguide end distancing from the objective lens with respect to θ1 and θ2 values

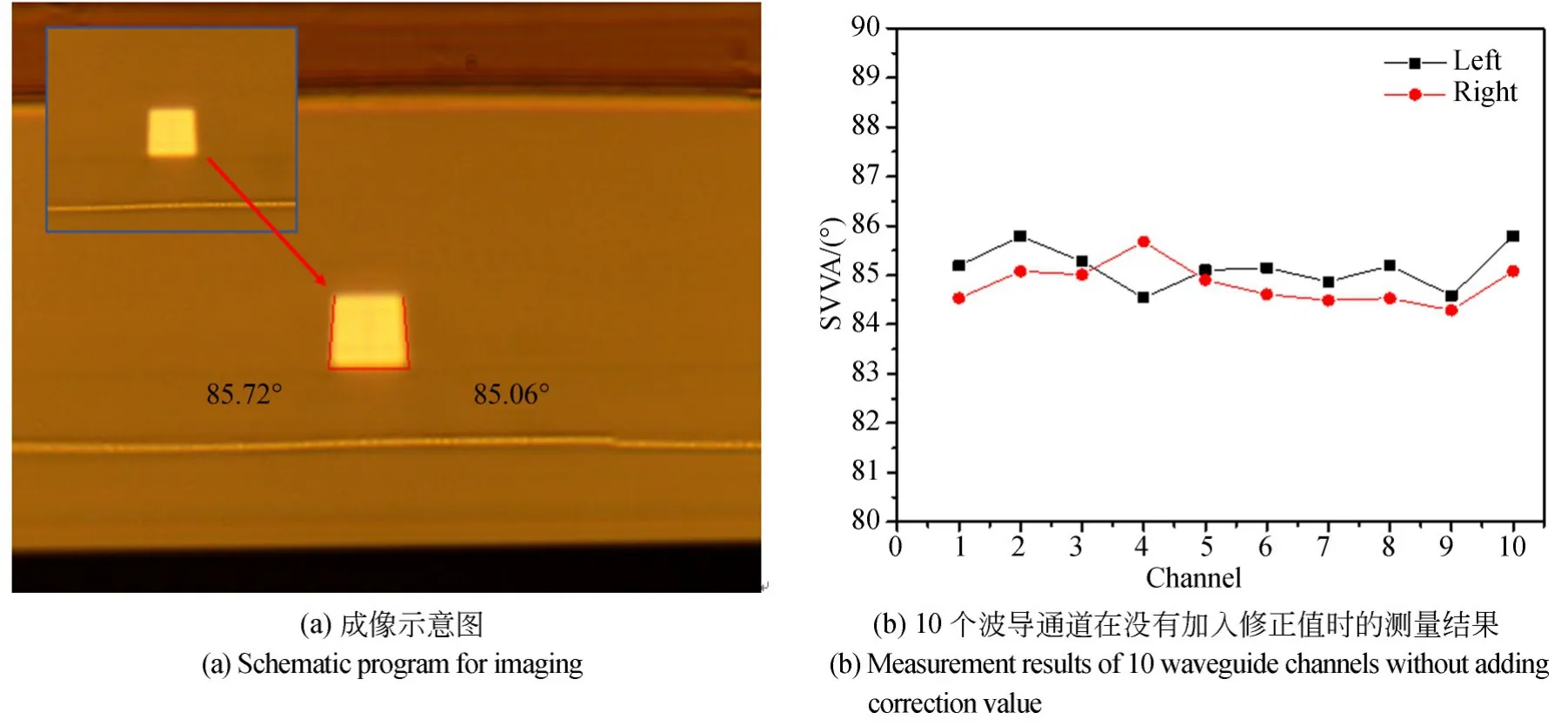
图6 SiO2波导端面光学显微镜测试Fig. 6 Measurement of end side of SiO2 waveguide by optical microscope

波导顶边远离物镜焦平面，波导端面由显微镜成像时侧壁角的变形要比波导顶边逐渐接近物镜焦平面时形变更为明显，因此该情况在光学显微镜下测量波导端面时应避免使用。角度增加的负值表示当波导端面远离物镜焦平面时图像的方法倍数迅速增加，因此测得的顶边宽度要比实际波导定边宽度值大。分析表明该方法得到的数值计算结果与实际情况相吻合。用显微镜图像测量波导末端倾斜角时，上述曲线可用于预估波导实际侧壁倾角。

4 实验结果与分析

根据上述数值模拟与分析方法所得出的结论，在满足加工均一性的前提下，制备了SiO2波导器件。由于模拟与分析过程中所设定的侧壁角度在实际测量中会产生较大误差，所以在实验中通过波导底部的侧壁角度互为余角的关系得出φ1和φ2。应用该方法对沉积包层后的10 个波导通道芯层的侧壁角度进行了测量，图6（a）为光学显微镜成像示意图，图6（b）是10 个波导在没有进行系统固有误差补偿时侧壁倾角的测量结果。

测量过程中，通过模拟分析法得出其误差角度为1°。作为对比，对同一晶片刻蚀SiO2波导未沉积芯层使用CLSM 进行沿波导顶面的逐层扫描测量波导侧壁角度，其中一个扫描重建结果如图7 所示，左右侧壁倾角分别为86. 8°和85. 3°。

10 个波导左右两侧SWA 的OIM 测试值如图8 所示，直立后波导倾角所引起的波导侧壁角度误差为1°。对每一个波导的两个角度取平均并计算测量容差后OIM 测得值与CLSM 所测值，结果如图8 所示。

图7 CLSM-LM710 测量结果Fig. 7 Test results of CLSM-LM710

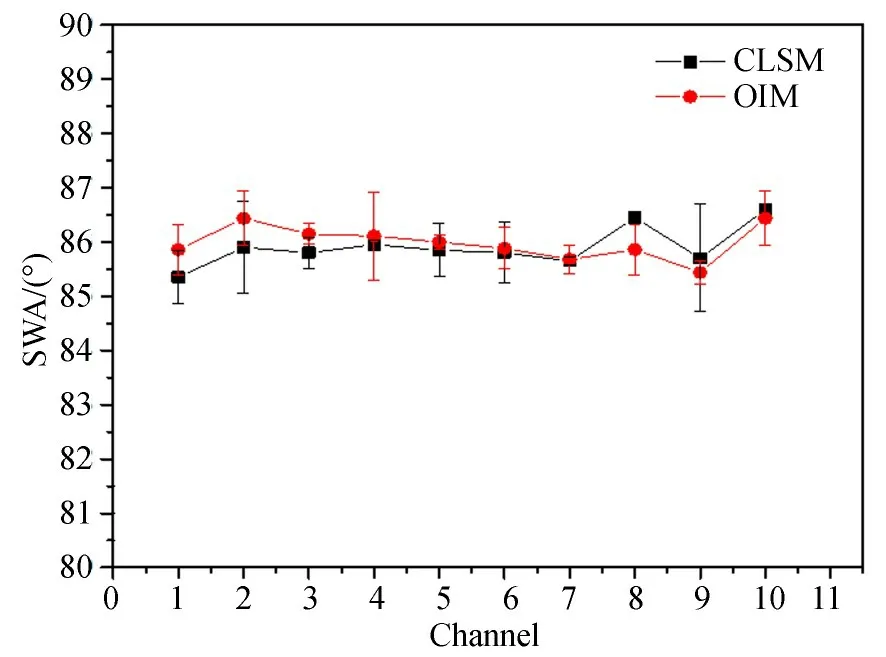
图8 OIM 测得添加误差量后的10 个测试值与CLSM 测试结果的对比Fig. 8 Comparison of 10 channels measurement results between added error range OIM and CLSM

5 结 论

本文根据SiO2波导结构和材料的特点，设计了通过光学成像显微镜测量波导芯层侧壁角度的方法，并对这种测量方法的精度进行了理论分析，对测量过程中的误差来源进行了详细的分析，提出了减小误差的测量方法，并应用光学成像显微镜测量实际器件。通过与激光共聚焦扫描显微镜测量侧壁角度的结果比较，获得了可信的波导轮廓和尺寸的测量结果。实验结果表明，光学成像显微镜测量波导芯层侧壁角度与激光共聚焦显微镜测量结果的测量精度差为±1°，在完成波导上包层沉积后的芯层侧壁角度测量方面具有较大优势。