非公共视场双目相机位姿标定

李勤文，倪首军，王志乾，李建荣，沈铖武，杨文昌，刘玉生

（1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春130033；2. 中国科学院大学，北京100049；3. 北京航天发射技术研究所，北京100076）

1 引 言

视觉测量系统由于其具有非接触，灵活性高，采集迅速等优点而被广泛应用［1］。在大多数视觉测量系统中，单台相机很难覆盖所有测量目标，而多相机系统具有比单个相机更大的视场，通常被用于获取大型物体或场景的几何信息［2-3］。决定多相机测量系统准确性的关键因素是相机之间的位姿关系标定。目前，多相机系统标定多利用额外的标定物，如平面棋盘格［4-5］或基于共线三点的一维标定物［6］来完成。然而当实际实验条件有限，无法借助额外的标定物且已有的目标特征点不足3 个时，现有的标定方法失效，需要寻求其他解决办法。

目前，双目相机位姿标定方法多是针对于双目立体相机，利用两个几何关系相对固定的相机以不同视角获取被测物体的影像信息，再利用同一个视觉信息在不同相机下的匹配特征不同进行相机标定，因此两相机之间要具有重叠的视场［7-8］。然而，在一些特殊的环境下，由于物体的遮挡或视场的限制，两相机无法获得重叠的视场，因此要进行非公共视场相机的标定［9-10］。目前，对无公共视场相机标定的研究可分为两类：一类是利用其他设备建立多相机视场之间的联系，如Long［11］和Wang［12］等人利用光学镜的反光特性对相机视场进行改善，克服了所有相机必须直接观察普通目标的局限，相机能够通过镜面间接观察目标。Sun［13］等人利用多组球面目标和高精度辅助相机对非公共视场相机进行标定。标定相机观测一组球体，辅助相机观测所有的球体。每个相机在各自的视场中重建球面中心后实现全局标定。另一类是利用标定物之间固有的位置约束关系进行相机标定，如Liu［14］等人利用两个相对位置关系不变的平面棋盘格组成复合目标对非公共视场相机进行标定。通过求解各视觉传感器坐标系到世界坐标系的关系，进而得到各视觉传感器之间的相对位姿。

本文针对自动对准系统中非公共视场的双目相机标定问题，不借助于高精度靶标或额外标定物，利用现有系统结构寻求两相机位姿关系标定的解决办法。通过多次移动标定物得到多组坐标数据的方法进行解算，由于相机视场范围有限，因此得到的目标点较为密集。然而，传统直接线性变换（Direct Linear Transformation，DLT）算法精度依赖于目标点的稀疏度［15］，为了克服DLT 方法的局限性，本文对DLT 求解方法进行了改进，并通过实验对比证明了本文方法的有效性。

2 系统概述

图1 双目相机标定系统示意图Fig. 1 Schematic diagram of binocular camera calibration

基于双目测量的自动对准系统如图1 所示，系统由位于上方部件上的两个光学测量装置A，B 以及位于底部部件上的两个合作目标点A，B组成。光学测量装置内含有光学测量相机和激光测距仪，底部部件长2 m，宽1. 5 m，测量范围为700～1 300 mm。测量过程中，2 个光学测量相机分别对底部部件上的合作目标点进行拍摄，得到点的图像坐标用于位姿解算，计算两部件的对准偏差，调整部件完成对准，在此过程中系统测量误差要＜2 mm。为了完成上、下两部件之间对准偏差的解算，需要对光学测量装置内的两个光学相机A，B 进行标定。然而，由于底部部件尺寸较大，两光学相机之间没有公共视场，因此需要考虑无公共视场相机的标定问题。为了尽可能利用现有系统完成两光学相机之间位姿关系的标定，摆脱传统的依靠高精度靶标或较多数量特征点的相机标定方法。本文利用两台莱卡经纬仪测量目标点在经纬仪坐标系下的坐标，进而对两相机之间位姿关系进行标定的方法。图1所示为标定系统示意图，以莱卡经纬仪1 的坐标系O-XYZ为公共目标坐标系，两个经纬仪通过交汇测量得到目标点A和目标点B在目标坐标系下的坐标。之后利用原有系统中的两个无公共视场相机分别对底部移动部件对角线上的目标点A和目标点B进行拍摄，得到点的图像坐标。利用得到的点在目标坐标系O-XYZ下的坐标和点的图像坐标进行相机标定。针对仅有两个目标点的情况，为了充分利用点的坐标信息，标定过程中保持上方部件和两经纬仪固定不动，即公共目标坐标系与两测量相机坐标系保持固定不动，通过多次移动底部部件，得到目标点A、目标点B的多组图像坐标和目标坐标进行两个无公共视场相机的标定。

3 非公共视场双目相机标定

图2 所示为非公共视场双目相机标定简图。在测量场内建立公共目标坐标系O-XYZ、相机A坐标系OCA-XCAYCA ZCA和相机B 坐标系OCBXCBYCB ZCB，各坐标系之间的位置关系保持固定。多次移动标定物，利用两台莱卡经纬仪测得目标点A，B每次移动后的坐标，分别为PiA=(XiA，YiA，ZiA)T，PiB=(XiB，YiB，ZiB)T，对 应 的 图 像点 坐 标 分 别 为pia=(uia，via)T，pib=(uib，vib)T，在 各自相机坐标系下的坐标为cia=(xia，yia，zia)T，cib=(xib，yib，zib)T，其 中i= 1，2，3，...，n。 为 了 标 定 两相机之间的位姿关系，需要先分别标定出相机A、相机B 到公共目标坐标系O-XYZ之间的外参数矩阵RA，tA和RB，tB，进而求出两相机坐标系之间的旋转平移关系RAB，tAB。

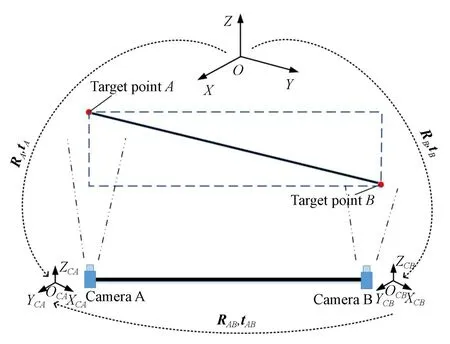
图2 非公共视场双目相机标定简化图Fig. 2 Simplified calibration diagram of binocular camera with non-public field of view

3.1 相机外参数矩阵标定原理

以相机A 为例，建立单相机成像方程：

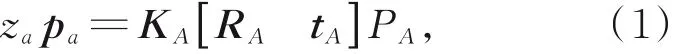
其中：za为标量系数；KA为相机内参数矩阵；[RA tA]表示公共目标坐标系到相机A 坐标系的转换矩阵，即相机的外参数矩阵，RA为旋转矩阵，tA为平移矩阵，表示为：

其中：α，β，γ表示公共目标坐标系到相机A 坐标系的旋转角。规定坐标系之间的转换关系，采用先平移后旋转的表示方式，用齐次坐标写成矩阵形式，得到：

其 中 ：i = 1，2，3，...，n，为 目 标 点 移 动 的 次 数 ；r11～r33表示矩阵RA内相应位置的元素。 经典DLT 算法标定单相机的基本原理是通过矩阵变换将式（4）整理为CM = D 的形式，其中：

C，D 中全部为已知量，M 为11× 1 的未知矩阵。当目标点移动次数n ≥6 时，可以列出的方程多于11 个，进而利用最小二乘法解得：

结合式（2）～式（5）可分离出相机A 到公共目标坐标系之间的外参数矩阵，同理可求出相机B 到公共目标坐标系之间的外参数矩阵。然而，由于两光学相机的视场范围有限实际测量中两目标点的移动范围也有限，目标点分布较为密集，使得经典DLT 算法的精度较低甚至出现病态解，影响标定精度，因此本文利用激光测距数据对DLT 算法的解算结果进行了改进。

3.2 基于DLT 的改进方法

在双目相机系统中增加激光测距仪，相机与激光测距仪的距离固定，相机光轴方向与激光测距仪的出光方向基本相同［16］。在标定后利用激光测距仪得到的一维数据，对由DLT 方法求得的相机的外参数矩阵RA，tA进行优化，然后利用Levenberg-Marquardt（LM）非线性算法进行全局求解，提高标定结果的准确度。

以相机A 为例，由3. 1 节方法求得的相机参数可以得到目标点A 在相机坐标系下的坐标，利用标定后的激光测距仪数据代替目标点A 在相机A 坐标系下沿光轴方向的坐标已知目标点A 两次移动前后在目标坐标系下的坐标为在相机A 坐标系下的坐标为相机光心为C，则有：

这里 的RA·表示将向量PiAPi+1A由目标坐标系空间转换到相机A 坐标系空间表示，RA为待优化的旋转矩阵，它是沿目标坐标系三轴的旋转角 α，β，γ 的函数，如公式（2）所示。()表示平面的法向量，若RA为真值，则在平面上，二者点积为0。因此可构造目标函数：

理 想 情 况 下V ( α，β，γ )= 0 ，然 而 由 于 测量噪声的存在，实际求得的RA不一定使式（8）为0。 为 了 最 小 化 式（8）的 误 差 ，用LM非线性优化方法对式（8）进行优化求解。 用以 指 导 优 化 方 向 的 雅 可 比 矩 阵J ( α，β，γ ) 表示为：

每次迭代过程中，目标函数V ( α，β，γ ) 的梯度为gk= JTkvk，k 为 迭 代 次 数 。 迭 代 步 长dk=数，迭代初始值 α0，β0，γ0可由3. 1 节求得的旋转矩阵反算得到。至此可以带入LM 非线性优化算法求解旋转角，进而得到旋转矩阵RA。

已 知 待 优 化 的 平 移 矩 阵tA=( ΔX，ΔY，ΔZ )T，由cia=( xia，yia，z′ia)T与PiA=( XiA，YiA，ZiA)T的关系：

可以得到：

其中r11～r33为由公式（8）求得的旋转矩阵RA中的元素。则公式（11）可表示为C1tA= D1，由最小二乘法可得tA=(C1TC1)-1C1TD1，从而可以得到优化后的平移矩阵tA。

为了保证解的准确性，防止相机外参旋转矩阵和平移矩阵各自优化有可能带来的局部解问题以及相机实际内参数值与标称值不符，进而影响外参求解精度的问题，通过最小化重投影误差的方法对相机内外参数进行全局求解。构造重投影误差函数：

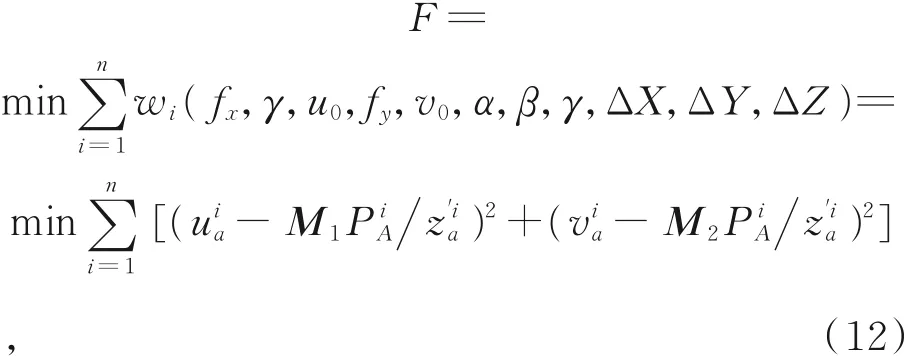
其 中 ：M1，M2表 示 取 投 影 矩 阵M 的 第 一 、第 二行，上标i 表示所有现存数据，[uiavia]T表示实际测得的图像点坐标。整个函数表示实际测得图像点坐标与空间点以（fx，γ，u0，fy，v0，α，β，γ，ΔX，ΔY，ΔZ）为参数进行重投影后得到的图像点坐标之差。 以给定的相机内参数值及由式（8）和式（11）求得的相机外参旋转角 α，β，γ 和平移距离ΔX，ΔY，ΔZ 为初值，再次利用LM 非线性算法对标定结果进行全局求解，可以得到优化后的相机外参数值，进而由式（2）和式（3）得到相机的外参旋转矩阵RA和平移矩阵tA。同理可求出相机B的外参旋转矩阵RB和平移矩阵tB。因此，按照先平移后旋转定义的相机B 坐标系到相机A 坐标系的转换矩阵为：

4 实 验

图3 所示为双目相机标定系统示意图，目标点A，B（如图4）的目标坐标系坐标由两台TM5100A 徕卡经纬仪通过交汇测量得到，点A，B 的图像坐标由光学测量装置A，B 进行测量，光学测量装置如图5 所示。光学测量装置包含有光学测量相机A，B 和两个激光测距仪，相机与激光测距仪的位置关系已知。 两光学相机采用MT9V032CMOS 数字图像传感器，像素尺寸为6 μm×6 μm，分辨率为400×400，相机焦距为35 mm。通过多次移动底部的移动部件，得到多组目标点坐标。然后对直接利用DLT 算法求解相机A、相机B 和公共目标坐标系之间的参数矩阵，进而得到两相机之间的位姿关系，与利用本文提出的方法对相机A、相机B 的外参数进行优化后得到的两相机的位姿关系进行对比，结果如表1 所示。

图3 双目相机位姿标定系统Fig. 3 Pose calibration system of binocular camera

图4 合作目标点Fig. 4 Cooperation targets

图5 光学测量装置Fig. 5 Optical measuring device

为了验证标定结果的准确性，利用求得的两相机之间的位姿参数，将相机B 坐标系下的目标点转换到相机A 坐标系下，计算两点之间的距离dAB，并与经纬仪测得的两点之间的距离tAB进行对比，将经纬仪测得的坐标值看作真值，利用公离误差的均方值，结果如表2 所示。由于实际地面不平整和底部部件微小变形的影响，实际测得两目标点之间的距离tAB有所不同。为了保证结果的准确性，在测量范围内选取10 组数据对相机A ，B 进行标定，得到两相机之间的位姿关系，之后选取另外10 组数据计算两目标点之间的距离与真值的误差。 从表2 可以看出，本文标定算法对两相机之间位姿关系标定的准确性优于DLT 方法，在系统测量范围700～1 300 mm 内随机选取10 组数据，求得目标点之间距离的均方差＜0. 2 mm，满足实际应用需求。

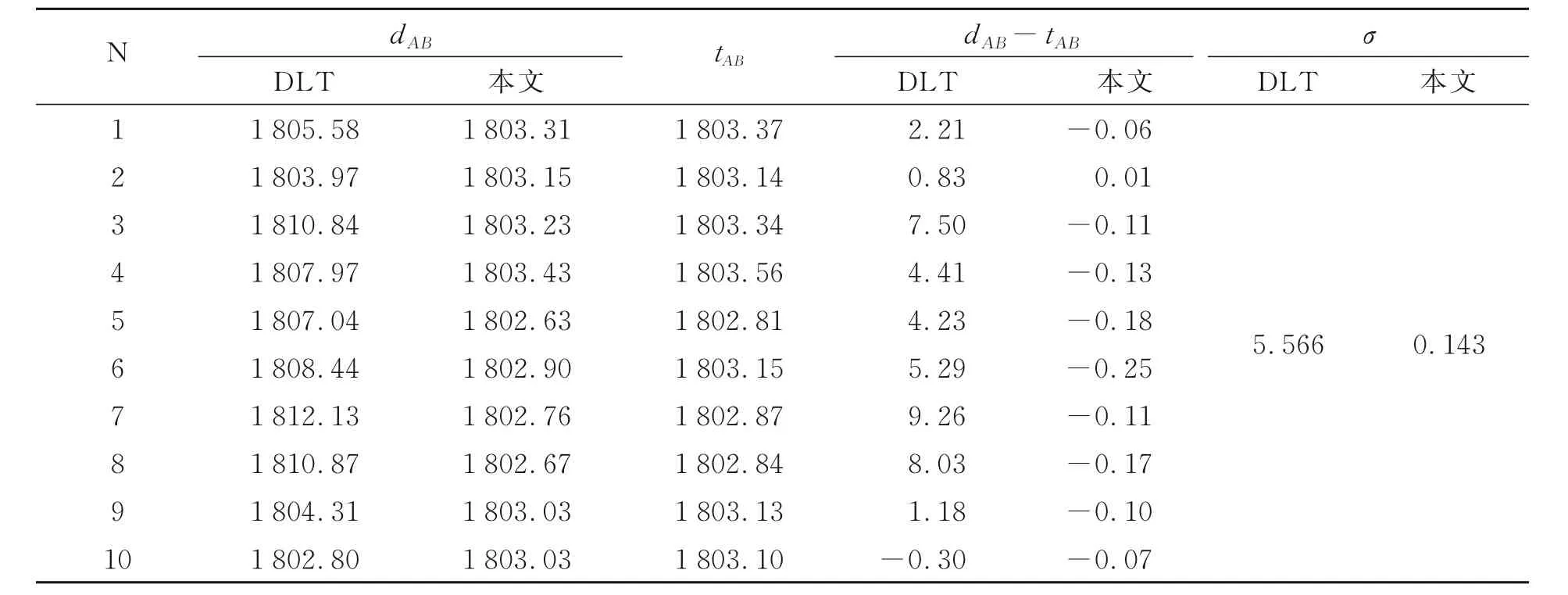
表2 由两相机位姿关系求得的目标点A，B 距离的均方差Tab. 2 Mean square error of the distance between target points A and B obtained from the pose relationship of the two cameras （mm）

表1 DLT 方法与本文标定方法结果对比Tab. 1 Comparison of DLT method and our calibration method

5 结 论

本文针对相机标定过程中目标特征点较少的问题，通过多次移动目标点得到多组数据进行标定，为双目相机位姿关系的标定提供了新思路。针对实际系统中两目标点移动范围有限导致的传统DLT 方法精度较低的问题，增加激光测距数据对标定结果进行优化，选取由两相机位姿关系求得的两个目标点之间的距离作为标定精度评价指标，以经纬仪测得的两目标点距离作为真值。实验结果表明，当相机与目标点之间的距离为700～1 300 mm 时，由本文方法求得的两目标点之间距离的均方差＜0. 2 mm，证明本文提出的非公共视场双目相机位姿标定方法是有效的。