不一般的相似——圆锥曲线中的位似关系

陈 峰

(江苏省苏州大学附属中学 215006)

在苏教版《普通高中课程标准实验教科书数学选修2-1》课本P74-P75中提出了一个很有意思的问题：尝试证明离心率相同的圆锥曲线“形状都相同”.如果上述结论成立，这意味着圆锥曲线中也存在着相似关系，为了弄清这个问题，首先必须引入位似的概念.

一、位似

两个多边形不仅相似，而且对应顶点的连线相交于一点，并且对应边互相平行或位于同一直线上，像这样的两个图形叫做位似图形(homothetic figures)，这个交点叫做位似中心，这时的相似比又称为位似比.

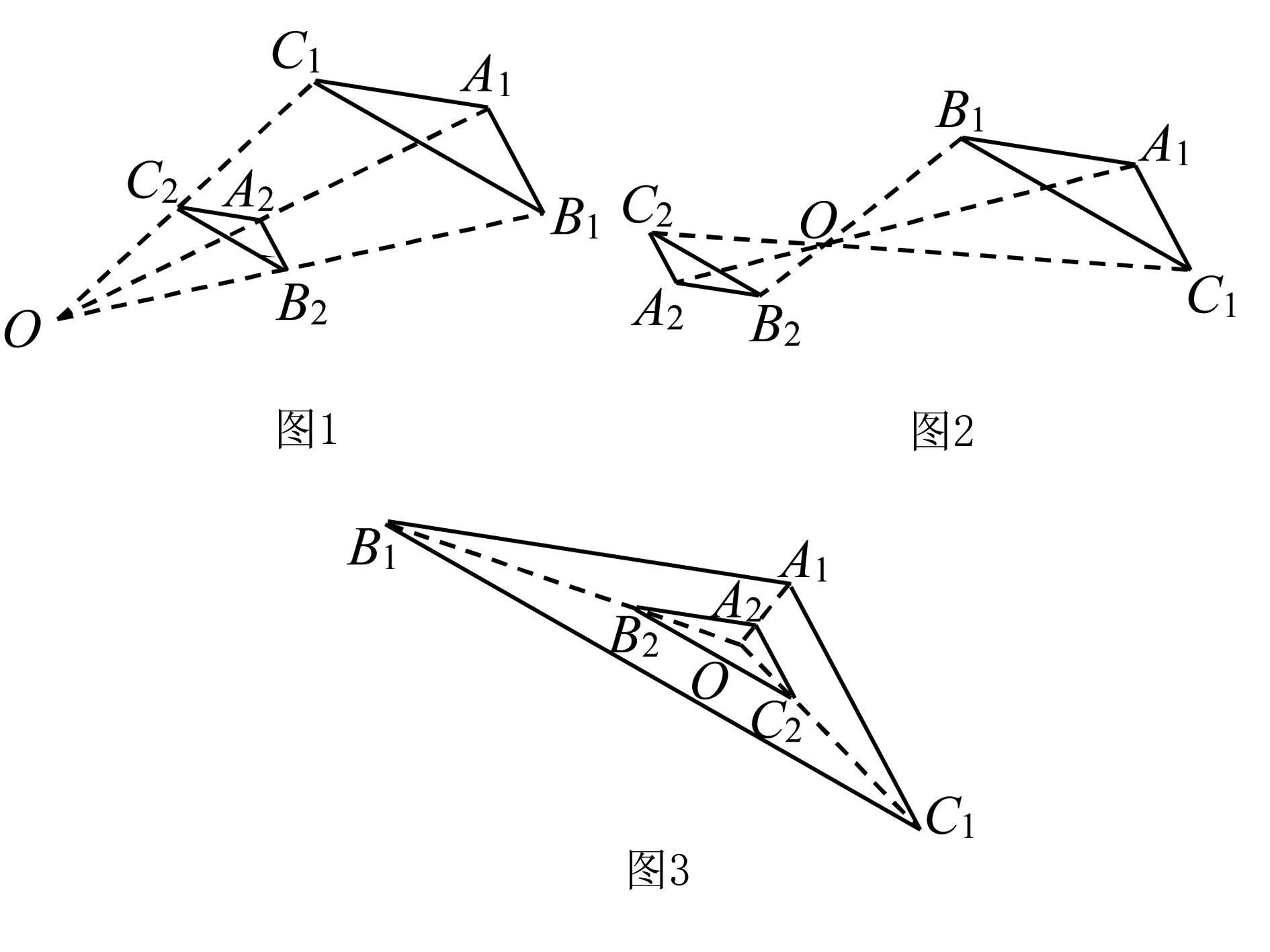
两个图形位似，它们的相对位置关系有三种：位似中心在图形的一侧(如图1)、两个图形分居位似中心的两侧(如图2)、位似中心在两个图形的内部(如图3).

根据位似的定义不难得出：两个图形位似则它们一定相似，而两个图形相似则它们不一定位似.同时，当两个图形位似时，除了满足相似的一切性质外，还满足一些特有性质，如“对应顶点的连线相交于一点”、“对应边互相平行或在同一直线上”等.

二、圆锥曲线的位似关系

1.抛物线

结论1抛物线y=ax2(a>0)与y=Ax2(A>0,A≠a)是位似图形，原点是位似中心.

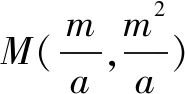
结论2抛物线y=a1x2(a1>0),y=a2x2(a2>0),…,y=anx2(an>0)是位似图形，原点是位似中心.

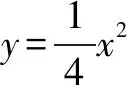
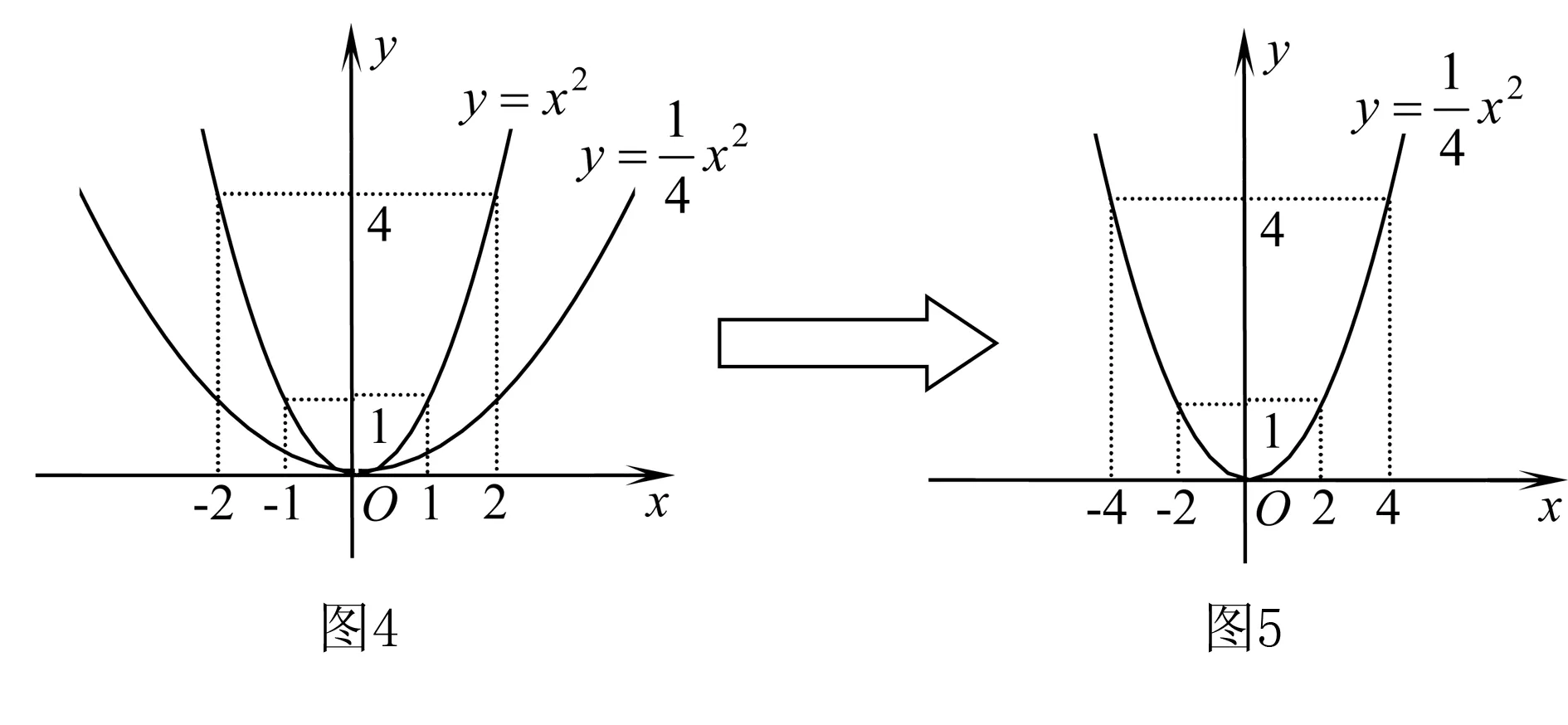
由结论3可知，抛物线的位似中心并不是唯一的，其顶点和焦点均可作为位似中心.

2.椭圆与双曲线

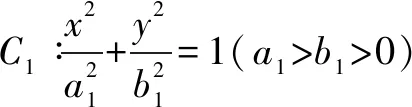
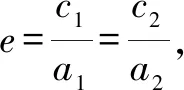
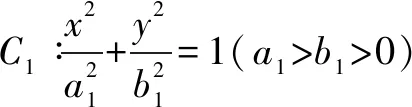
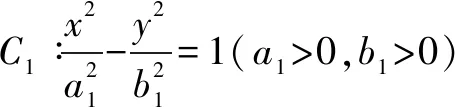
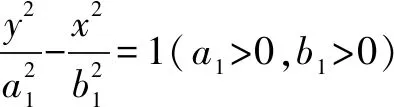
3.圆锥曲线的统一形式

当01时，方程(*)表示双曲线.

结论6离心率相等的圆锥曲线C1,C2是位似图形，反之，若圆锥曲线C1,C2是位似图形，则它们的离心率相等.(证明略)