除法竖式推导应与直观操作结合

廖文武

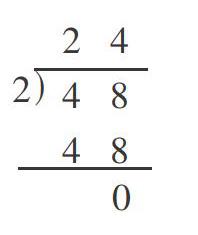
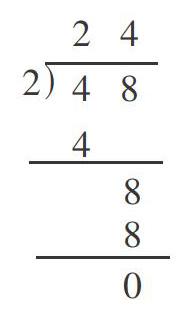
[摘 要]“除数是一位数的除法”是北师大版教材第五册中的内容，属于计算教学范围。按照课程标准的总体要求和布局，这部分内容是第一学段中最精深的计算知识。那么，指引学生探究笔算除法的算理，体验笔算除法的详细过程，带领学生实现从算理到算法的转型，便成了教学的重难点。

[关键词]除法;竖式;算理;笔算

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）02-0074-02

“分桃子”这一内容是“除数是一位数的除法”的第一课时。教学时，许多教师不解的是学生在笔算时，出现了许多稀奇古怪的竖式，如右图。在后续的教学中，无论教师如何劝导，学生还是先直接口算出结果，然后将结果转移到竖式上商的位置，再照抄被除数。这样频发的状况让教师无奈重启旧模式，一再重申竖式的标准格式，经历几天的强化训练之后，学生才能纠正不良习惯。究竟怎样才能让学生牢固掌握笔算除法的算理，实现高效计算呢？笔者认为，教学除法竖式时，应当在问题情境的任务背景下进行直观操作演示。下面笔者就通过实际教学来说明如何让学生对笔算除法的算理进行科学构建。

【教学案例一】

师 （出示课件：猴子分桃子）：鲜美的桃子熟透了，掉了满地。有2只猴子看到地上的桃子，便迫不及待地将它们捡起来，清点一下，一共有48个。桃子是被2只猴子同时发现的，见者有份，于是它们想平分这48个桃子，到底该怎么分呢？我们来帮帮他们吧。（板书课题：分桃子）

（本节课的主要目标是研究并学习笔算两位数除以一位数的除法的算法，因此，不必拐弯抹角，可以直接提问列式，从而节省课堂时间）

师：接下来，你们可以根据个人喜好自由选择方法进行研习，可以拼摆演示，也可以直接笔算。

生1：我把小棒当成桃子，每只猴子先平分捆摆放的2捆，再来平分零散放置的4根，这样一来，每只猴子分到手的共有24根。

（注：此种操作法实际上是为除法竖式建立直观表象，教师可让选用这种操作方法的学生优先展示汇报。当学生汇报时，教师可以密切配合学生，用课件演示分配小棒的动态过程。学生观看课件演示后，教师询问学生前后一共分了几次小棒，先分配哪里的小棒，再分配哪里的小棒。）

生2：我用的是口算法，先口算十位数除法，40÷2=20，再口算个位数除法，8÷2=4，最后将两次相除的商相加，20+4=24，所以48÷2=24。

生3：我用的是列竖式的方法来计算的。

（注：教师此时要让学生上台演示，引导学生写出竖式）

师：你能解释一下这个竖式是怎么算的吗？

生3：先从十位除起，因为40÷2=20，所以把商2写在十位上，再来除被除数的个位，8÷2=4，把4写在个位上，2×24=48，所以48÷2=24。

师：非常好。谁看懂了这个竖式？一共进行了几次除法演算？

生4：一共除了两次。

师（用不透明的纸板先遮住数字8，露出数字4）：先算哪一步除法？

生（齐）：4÷2。

师：被除数里的这个4对应到小棒里代表4捆小棒，4÷2=2，商2就代表2捆小棒，拆解后就是2个十根，所以第一次除得的商写在十位上。

师（用不透明的纸板遮住数字4，露出数字8）：这次算哪一步除法？

生（齐）：8÷2。

师：这个8对应到小棒里就是8根小棒，8÷2=4，商4代表4根小棒，所以第二次除得的商写在个位上。

这实际上是教师讲解竖式计算格式和算理的重要举措，纸板的作用不容小觑，两次使用纸板遮挡关键数字，将十位和个位的除法运算分开来，使学生深刻理解竖式的计算流程是十位和个位的单独相除。

【教学案例二】

师：这2只猴子正准备分桃子，忽然来了1只猴子。还是这48个桃子，现在要平均分给3只猴子，此时，每只猴子能分到几个桃子？

生1：48÷3=16（个）。

师：请大家用小棒摆一下，边摆边思考，把48平均分成3份，具体怎么操作？根据分配的流程列出竖式。

生2：我先分4捆小棒，每只猴子只能分得一捆，剩下一捆反映到竖式中，就是先用被除数十位上的4除以3，4除以3商l，代表一整捆，所以1写在商的十位位上。1×3=3，把3写在4的下面，代表4捆里面已经分掉了3捆。4-3=1，代表还剩一捆不够分也没有分，把个位上的8下移，和剩下的一捆合起来，就是18根，再来二次相除，18÷3=6，每只猴子分得6根，把6写在个位上。

师：找出48÷2与48÷3竖式的不同点和相同点。

生3：不同点是48÷3十位上除完后有余数，要把个位数字添上去继续除;相同点是都是从高位除到低位。

【教学反思】

1.注重直观操作与算理探究互相对应，引导学生将算理应用到算法中。尽管教师没有给出“除数是一位数”的笔算方法，但学生能够概括出一个基本模式，知道笔算的基本流程和操作步骤，运算逻辑十分严密。因此，教学时教师有必要将直观操作与竖式推演结合起来，揭示竖式的算理，使本节课的难点得到突破。

2.控制好时间配比，注重课堂效率。众所周知，自课程改革以来，教师热衷于创设情境，钟情于探究，但弊端明显，那就是耗时较多。而学生的注意力的持续时间有限，过于丰富的情境故事会分散学生注意力，超额占用课堂时间，导致计算训练时间被占用。因此，巧设情境，单刀直入探查48÷2的算法，并在匯报交流算法时，对传统算法一语带过，集中精力专攻直观操作与笔算竖式，并进行辨析，更能使学生深刻理解，避免学生产生困惑和犯错。

3.课堂气氛活跃，充满童趣。“分桃子”的故事吸引了学生，最后又续编故事进行拓展，激发了学生的学习兴趣。

4.扶放结合。两步计算的除法竖式是新知识，有一定难度，师生共同探究竖式的算理，并一直坚持操作演示与竖式推导并举，减轻了学生的负担。而在教学48÷3时，教师则是大胆放手让学生自主探究，使之在操作、讨论中学到知识、习得技能。这样由扶到放、逐步递进，将难点逐一攻破。

5.对本节课的难点处理得当，帮助学生深化了算理。

（责编 黄 露）