以问导学

何丽

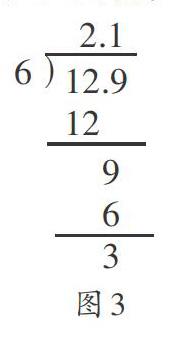
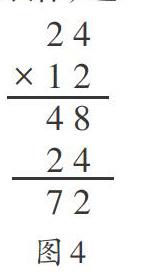
[摘 要]思维自疑问和好奇开始，在“课始、课中、课尾”三个关键时段，围绕“意义、算理、算法”三个核心要素，促生疑，巧推动，唤醒学习需求，实现从接受既定任务到自觉思维行动的转变;推动深度理解，实现从单纯关注结果到深度探寻算理的转变;建立知识联结，实现从只见树木到渐现森林的转变。

[关键词]问题;深度学习;计算教学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）02-0004-03

计算在小学数学中占据着相当大的比重，贯穿六年数学学习始终，计算教学是培育核心素养最基础层级“运算能力”的主阵地。我们尝试围绕“意义、算理、算法”这三个核心要素，在“课始、课中、课尾”三个关键时段，引学生质疑，借问题推动，以此作为深度学习计算的驱动码，唤醒学习需求，促进深度理解，建立知识联结。下面以人教版教材四年级“小数加减法”一课为例进行阐述。

一、课始之问，唤醒学习需求

【教学片段1】

师（出示图1）：我家吊灯的灯泡坏了，得换下来，够不着，怎么办呢？

生1：可以把旁边的凳子拿过来，站在凳子上试试。

师（出示图2）：能说说具体思路吗？

生1：把凳子的高度和您的身高加起来，再把结果和2.51米比一比就知道了。

师（将算式1.65+0.59写在黑板上）：仔细观察这个算式，你有什么发现？有什么问题？

生2：加数都是小数，而且是两位小数。

生3：两位小数加两位小数该怎么算呢？

（教师板书：两位小数加两位小数   怎么算？）

……

“创设情境—提出问题—列式解答”是多数计算课开启新知的基本程序。本课多了一个环节：看新建的算式与以往有何不同，问将要探究的问题是什么。数十秒的时间，一问、一思、一答、一发现，引发的变化却如蝴蝶效应般，学生从 “教师安排什么就做什么，教师讲什么就听什么”，变成了大胆质疑“学什么？为什么学？”，自明方向，自主探寻。需求被唤醒，成为动力之源。

起步之初，如何引发疑问，唤醒学习需求？

1. 创现实场景。计算内容大多是按单元来呈现，上例就是人教版教材四年级下册第六单元的第一例，此后所学都是在此基础上的延伸，如不同位数的小数相加减、小数加减混合运算等。类似这样的种子课，可以熟知的场景、现实的问题、真实的数据承载新知，借助觀察发现所学的内容“加数都是两位小数”，通过比较，拓展知识 “相关数据不再限于整数”。细思四则运算，从整数到小数，直至分数、百分数，大多因解决实际问题而生，承载的现实场景亦信手可得，教师所要做的就是让学生自然体会到并非为算而算，而是因需而学。

2.造认知冲突。巧设认知冲突是引发质疑的一种有效方式。比如乘法分配律一课，课始师生开展“两位数乘99”的计算比赛，一些学生担任主考官来出题，其余学生则使用计算器与心算的教师角逐。一场本不公平的比赛，学生似稳操胜券，但结果却出乎意料，任意报出一个两位数，数秒之内，学生尚未在计算器上输完，教师已说出答案，而且各个精准。当不甘、懊恼、沮丧等各色表情出现在屡战屡败的学生脸上时，一个疑问也呼之而出：“老师一定是用了什么技法！里面藏着什么规律？”探究聚焦此疑问展开。在混合运算及一些规律性计算的教学中，教师均可这般设陷阱、布迷阵、造冲突，引学生入愤悱之境，诱学生展心中所惑，促学生行主动探究。

3.引观察比较。教材关于计算的内容多是按照一定的逻辑顺序编排，比如三年级“两位数乘两位数”这一单元，例1的“24×12”不需要进位，例2的“24×53”出现进位，再至例3的“32×30”乘数末尾有零，从一般到特殊，逐个递进，分课呈现。在解读例2情境并列出算式之后，可指导学生观察：“看着这个算式，有什么想法？”细看、静比之后，学生会提出“怎么又是两位数乘两位数，不是刚学过吗？会遇到什么新问题呢？”百思不得其解的学生已无须教师多言，自觉用已经掌握的算法边试边寻，进而发现有进位，“进位怎么处理？需要注意哪些问题？”便成为学生关注的焦点。再至例3的算式“32×30”，无须教师发问，学生脱口而出：“要是乘数末尾有零该如何计算。”种子课之后的生长课多能这般。

计算须会其意，问起而意显。课始之问，实现了从接受既定任务到自觉思维行动的转变。

二、课中之问，推动深度理解

【教学片段2】

（学生算出1.65+0.59的结果后展示、汇报）

生1：先用5+9得14，百分位上写4，向十分位进1，再算6加5加1等于12，十分位上写2，向个位进1，最后算1加1得2，计算结果为2.24。

师：有人对这个计算过程有疑问吗？

（学生或面面相觑，或沉默不语，或欲言又止，数十秒的静寂之后开始举手）

生2：能不能从十分位开始算呢？

生3：进位的1究竟写在小数点左边还是右边？

生4：为什么5和9可以直接相加呢？

……

“自主尝试—汇报展示—评议正误”是多数计算课建构新知时的常态环节。本课的不同在于及时抛出“有人对这个计算过程有疑问吗？”原本欣喜于轻松迁移，满足于一致结果的学生，回顾过程，掀起波澜。问题最为真实，直指核心：“能不能从十分位开始算呢？”所涉及的正是“从最低位加起”，数位多了，从哪里开始;“进位1写在哪里？”似乎无关紧要，实则正是“哪一位相加满十就向前一位进一”的理解之机——哪来的1？为什么可以向前一位进1;“5和9相加”，借的是一位小数加减法的惯性，为什么？……这些问题，推动了深度理解。

建构之中，如何引发疑问，推动理解？

1.捕捉困惑，引问。有时学生的尝试并不顺利，甚至会遇难而止，无功而返。教师便可通过巡视，及时发现、敏锐捕捉、巧妙展现。如小数除以整数“12.9÷6”，相当一部分学生算到十分位有余数后就着笔难下了（如图3）。

师：这样可以吗？该怎么继续呢？

生1：在3的后面添上一个零，继续往下除。

师：为什么可以添上零？

生2：在小数末尾添上零或者去掉零，小数的大小不变，这是小数的基本性质。

师：添上零以后商写在哪？

生3：在3的后面添上零就从3个十分之一变成了30个百分之一，除以6得到5个百分之一，所以5写在百分位上。

问题不断提出，对话充分展开，疑惑轻松化解，算理就此明晰。

2.“无事生非”，追问。学生的尝试大多借助知识迁移，或是直觉判断，在意于答案是否正确，对于算理鲜有关注。比如前例的两位小数加两位小数，学生有一位小数加减法的学习基础和探究经验，又因加数的位数相同，自然而然就对齐了数位，从百分位开始加，在得数处对齐加数的小数点后补上小数点，至于其中之理并未深思细查。当被问及“有什么疑问？”时，学生才开始积极寻找答案。如“为什么相加满十可以向前一位进一”，或是从元角分的角度去说明，或是根据计数单位间的关系来解释，不同的学生，不同的视角，不同的表征，殊途同归，“因为小数相邻计数单位间的进率都是10，所以算小数部分时和整数一样逢十进一”。“无事生非”的追问，使学生不再停于表面，而是知其究竟，更添了一分追根溯源、寻其本质的意识。

3.将错就错，诱问。学生在尝试中可能出错，遇此情形，教师要捕捉资源，鼓励学生直面错误，大胆质疑。比如两位数乘两位数24×12，有学生给出如图4算法：

教师提问：“有问题吗？”于是便有了学生的各抒己见：24乘10就等于240了，24乘12怎么可能是72这个结果，应该比240大;第二次乘的不是1，它在十位上，表示的是1个十，所以乘得的积是240，因此2要写在百位上，4要写在十位上……争着辩着，理就明了。有人发问，更多的人在思考、分析，用各自擅长的方式尽述其理。

计算须明其理，问起而慧生。课中之问，实现了从单纯关注结果到深度探寻算理的转變。

三、课尾之问，建立知识联结

【教学片段3】

师：这是赵老师7到10岁时的身高，哪一年身高增长得最快？……

师：全国10岁女生的标准身高约为1.4米，赵老师和10岁女生的标准身高相差多少？

生1：用1.4-1.34就知道了。

生2：这个算式和之前学的不一样，怎么算呢？

师：这是个重要发现，还有什么新的疑问吗？

……

“应用、总结”是课尾必不可少的一步，本课的练习看似常态，应用所学知识解决实际问题，实则玄机暗藏。课中涉及的均是两位小数加减法，此练习最初也是有针对性的，随着一个信息的出现“标准身高约为1.4米”，学生的疑问如开闸般奔涌而出：“一位小数减两位小数，怎么算？”“解决问题中一定会出现位数不同的情况，算法又如何？”“如果是小数与整数相加减呢？” ……这些问题让知识不再只是散落的点，而成关联密切的线，纵横相接的网。

总结之时，如何引发疑问，建立知识联结？

1.疑生纵深发展处。聚焦知识的生长点，设一个情境，做一番鼓动，带来的将是学习内容的自然伸展，从“小数位数相同的加减法”到“小数位数不同的加减法”，直至跨数集的相加减，引起的是学习方式的自主改变，不是无为地等待下节课的到来，也不是遵守教师先学后教的规定，而是自我需求推动下的自主探寻：自己举几个不同的例子;试着用已有的方法去算一算，当想到在一位小数末尾添零补齐数位时，一切豁然开朗，原来转化使新问变旧颜;算完后再观不同的算式，方法的相同之处一目了然。待到此时，将探究所得、个人理解外化成语言与伙伴交流、与大家共享，已成学生最强烈的期待。细思计算教学，大多能如此，比如学了同分母分数加减法，向纵深处多想半步“如果是异分母分数加减法呢？”“如果是分数乘法呢？” 知识在疑问中生长。

2.问在横向关联处。找准知识间的关联点，增一个环节，行一些引导，带来的将是学习的深度发生。比如本课末将整数加法、同分母分数加法和刚学的小数加法三例展于一处：

“三类计算有何不同，又有什么关联？”课似将止，而疑又起，就这样，神秘的面纱在探寻中一点点被撩起，“整数的末位对齐，小数的小数点对齐，分数的分母不变”这些显性的不同，其实都源于它们本质上的相同——将相同计数单位的个数相加。对疑问的探索实现了知识间的整体联通，融入了原有的认知体系，长进了新的结构之中。

计算须现结构，问起而线明。课尾之问，实现了从只见树木到渐现森林的转变。

思维自疑问和好奇开始，“以问导学”教计算，不仅增课堂之趣，提教学之效，更重要的是经此驱动，需求成为动力，理解成为基础，结构成为目标，深度学习真正发生。

（责编 金 铃）