渗透数形结合思想，提升教学质量

张芸

[摘 要]在小学数学教学中，教师不仅要让学生掌握数学知识，还要培养学生的数学思维。运用数形结合的思想，有利于降低学习的难度，帮助学生加深对数学知识的印象。教师需要在教学中更好地渗透数形结合思想，使学生了解数学基本概念，掌握数学学习规律，厘清解决问题的思路，培养学习能力，打造高效的小学数学课堂。

[关键词]教学质量;数形结合;数学思想

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）02-0053-02

随着新课程改革的推进，在当前的小学数学教学中，以人为本的教学理念逐渐深入。小学阶段的学生对于事物的认知水平比较低，遇到一些较难的数学问题时会感到无从下手，这不利于数学教学活动的开展。数形结合思想可充分发挥数字和图形相互转换的优势，降低学生学习的难度，提高数学教学的效率。

一、数形结合思想的内涵

数学是一门以数量关系和空间关系为主要研究对象的学科。小学生的思维层面较浅，主要停留在直观思维层面，许多学生在学习数学知识时会感到困难。小学数学课本中有很多数字和图形出现，将这两者相结合进行教学，可培养学生数形结合的思想，使学生对知识的理解更深刻，从更深入的视角认知数学。数形结合主要表现为数量关系和空间关系相互转换，而这也是学生抽象思维和具象思维进行转换的过程。数学学习更侧重于方法的学习，学生在具备了数形结合思维之后，也会更易于掌握数学知识，使学习效果得以提升，对于他们思维能力的培养很有帮助。

二、渗透数形结合思想的必要性

1.有利于降低知识的难度

小学数学教学主要是培养学生数学学习兴趣，为难度更高的数学学习打好基础。小学生的理解力普遍较差，面对一些抽象的数学问题时，容易丧失学习的自信心。而教师在讲解的时候运用数形结合思想，就可以让学生直观感受数字与图形之间的关系，降低学习的难度。

2.有利于加深学生对知识的理解

受到理解能力和知识结构等因素的限制，小学生在理解一些复杂的数学问题时比较困难，在做题时会厘不清解题思路，而利用数形结合就可以把数学语言用图形的形式展示出来，使得数学内容更加形象化，有助于加深学生对学习内容的印象。

3.有利于调动学生的主动性

将数字和图形相结合会使得数学更加具有感染力，消除学生与数学之间的隔阂，这样学生更愿意主动学习，在探索中掌握数学知识。如鸡兔同笼的问题就是将数字和图形相结合的一个典型案例，利用数形结合引导学生进行推理，就能提高学生的学习积极性。

三、数形结合思想应用案例分析

1.抽象概念直观化

数学概念是小学数学教学的基础内容。由于大部分数学概念比较抽象，学生在理解的时候就会出现一定的困难。教师为了使概念教学的过程简便化，会让学生死记硬背一些定理和定义，学生也因此无法了解知识的由来。这样就会导致学生无法灵活运用所掌握的知识解决数学问题。要想改变这种局面，教师需要巧妙地将数字和图形相结合，使抽象的数学概念直观化、形象化，促进学生对数学概念的理解。例如，在讲解“分数的意义”这部分内容时，就可以运用数形结合思想，先让学生预习课本上的内容，再引导学生学习。

师：大家预习后有什么收获？

生1：我知道了分数的定义。

生2：我知道了分数的意义。

师：好的，那么请生2给大家说一说分数的意义。

生2：分数就是把一个整体分为好几个部分，用来表示某几部分的一个数字。

师：说得很好，还有谁想谈谈预习的收获？

生3：我知道了哪一部分是分子，哪一部分是分母。

……

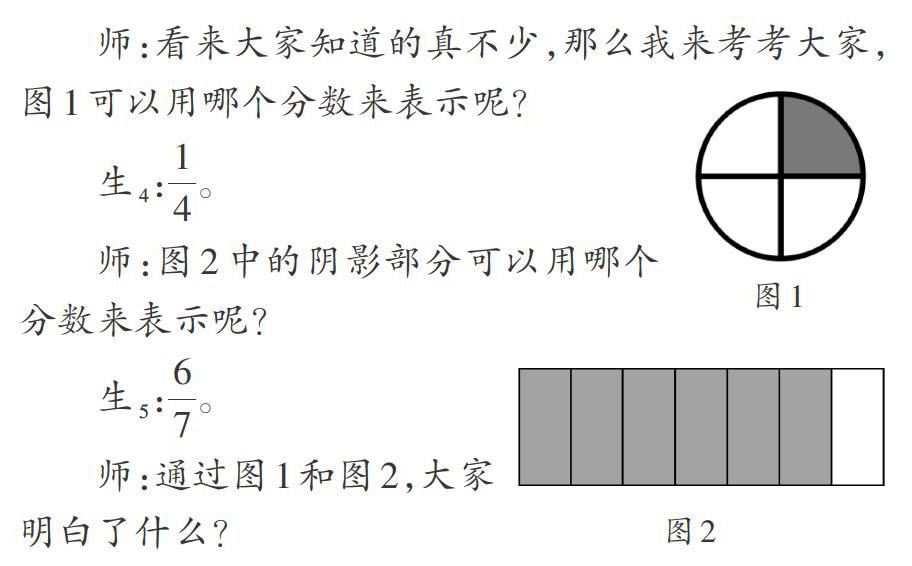
师：看来大家知道的真不少，那么我来考考大家，图1可以用哪个分数来表示呢？

生4：[14]。

师：图2中的阴影部分可以用哪个分数来表示呢？

生5：[67]。

师：通过图1和图2，大家明白了什么？

生6：分数表示总体和部分之间的关系。

在这一教学环节当中，学生掌握了分数的基本概念，能利用图形来表示分数，学会将图形和数字相对应，进而掌握数学基本概念。

2.隐形规律形象化

在小学数学中，许多数学规律都是比较隐蔽的，利用数形结合的形式可以将隐蔽的数学规律形象化。对于一些数学公式时，推导的过程也是學生进行数学思想建构的过程。一些学生并不重视公式的推导，对于公式的学习仅仅停留在背诵层面，忽视公式背后的数学规律。要想有效地避免学生生搬硬套，使他们能灵活地利用数学公式解决实际问题，教师可利用数形结合的形式辅助教学。例如，在教学“三角形的面积”时，为了让学生了解三角形面积计算公式的由来，教师通过数形结合的形式开展教学。

师（出示图3）：哪一位同学能用长方形的面积公式来求解图3中三角形的面积？

生1：6×8÷2=24。

师：6×8表示什么意思？

生2：可以看作两个完全一样的三角形拼成的长方形的面积。

师：为什么要“除以2”呢？[]

生3：因为三角形的面积正好是长方形面积的二分之一。

师：（出示图4）：请用同样的方式求出图4中三角形的面积。

在这一过程中，教师结合图形向学生展示了三角形计算公式的由来，使学生了解三角形面积与长方形、平行四边形面积之间的关系。通过数形结合的教学环节，学生了解了数学公式背后的数学规律。

3.复杂问题简单化

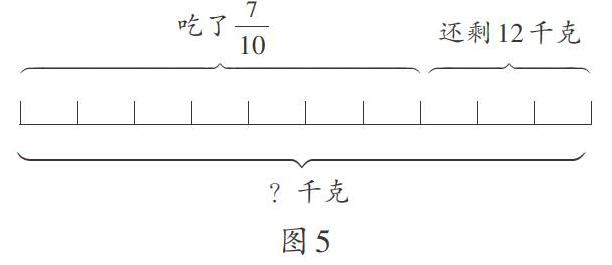
应用题考查的是学生应用知识解决问题的能力。一些学生在做应用题时感到毫无头绪，很难找到题目中的数量关系。为此，教师可以利用数形结合思想，把题目当中的文字转化为图形，帮助学生厘清解题思路。例如，小明家里有一袋小米，他们已经吃了[710]，袋子里还剩下12 kg，请问这袋小米买回来的时候有多重？

在解这道题时，教师可以让学生利用画图的形式找到题目当中各个量之间的关系。从图5可以看出已吃小米和剩下小米之间的关系，可以得出已经吃了[710]，还剩下[310]，那么剩下的[310]就是12 kg。至此，学生利用已经掌握的分数知识就可以轻松解答这一问题。通过数形结合的方式，就可以让学生轻松找到题目当中数量之间的关系，解决一些较为复杂的分数问题，化繁为简。

4.解题方法最优化

数字和图形是数学的基本元素，可以说数字和图形相互影响，共同推动了数学的发展。在日常教学中，有些数学问题不是简单地以形助数或以数辅形进行数字和图形的转换就可以解决的，教师应当引导学生从已知的数学条件和未知的结论出发，找到各个量之间的关系。例如，一个圆柱体的底面半径是10 cm，如图6所示，把它切割并拼成近似的长方体后，表面积增加了200平方厘米。请问这个圆柱体的体积是多少？

师：要想求出这个圆柱体的体积，需要知道哪些条件？

生1：需要知道圆柱体的底面半径和高。

师：底面半径在题目中已经给出了，那怎样求出高呢？利用“增加的表面积”这个量可不可以计算出高？

生2：增加的表面积是长方体左右两个侧面的面积，这个面积可以用底面圆的直径乘以圆柱的高计算得出。

可见，在解决一些几何类的抽象问题时，利用数形结合找到解题的突破口，可使解题方法最优化。

在数学教学中，教师运用数形结合的思想，使抽象的概念直观化、隐形的规律形象化、复杂的问题简单化，提高了教学效率。此外，教师还要结合具体的案例灵活地进行教学设计，使数形结合的思想能更好地融入课堂教学中，打造高效小学数学课堂。

（责编 罗 艳）