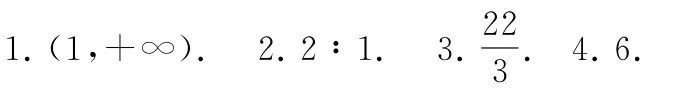浅析平面向量在解题中的应用
◇ 北京 张 辉
求解向量问题最基本的思想是基底思想,将所求向量用恰当的基底向量表示,就可以通过基底向量的运算求解;建立恰当的平面直角坐标系,又可以将向量用坐标来表示,通过坐标运算来求解,将向量的运算转化为坐标运算也是解决较难向量问题的通法.本文通过几个典型例子,谈谈这两种重要方法在解题中的应用.
例1如图1,在矩形ABCD中,点E为BC的中点,点F在边CD上,若的值是( ).


图1
解法1利用基底的思想,将用基底向量表示.
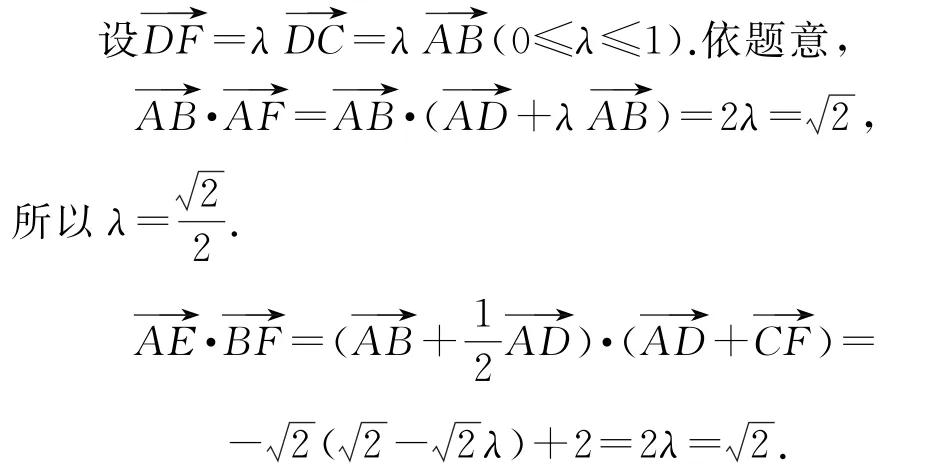
故选C.
解法2建立平面直角坐标系,将问题转化为向量的坐标运算.
以A为坐标原点,AB,AD所在直线为x轴和y轴建立平面直角坐标系(如图2),则.
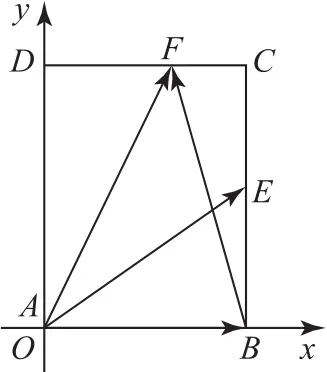
图2
点评
例1用两种方法解决了向量数量积的问题,基底法要注意通常选择向量夹角已知、模已知的两个向量作为基底;当所给图形便于建系时,可以采用坐标法使得问题迎刃而解.
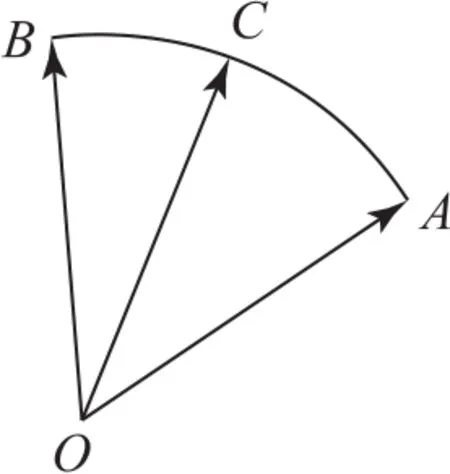
图3
例2给定两个平面单位向量,它们的夹角为60°.如图3所示,点C在以O为圆心的圆弧上变动.若,其中x,y∈R,则x+y的最大值是________.
解法1利用基底的思想夹角、长度已知,所以作为基底的条件是具备的.平方后可以将向量转化为模,再利用不等式的性质求解.
解法2建立平面直角坐标系,将问题转化为向量的坐标运算.
以O为坐标原点,OA所在直线为x轴建立平面直角坐标系(如图4),则
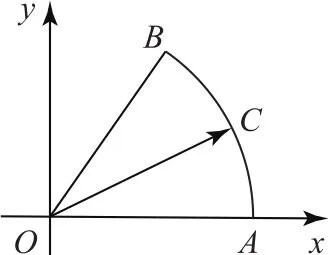
图4
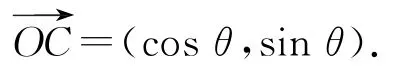

解法3由分析2中式①得

点评
例2中的解法1是利用基底的思想加以解决,用到了处理向量问题时常用的“见模平方向量”方法;解法2、解法3利用了坐标法,最终将求x+y的最大值问题利用基本不等式加以解决或是引入角参数减少变量加以处理.建立平面直角坐标系后就可以将向量问题代数化,使问题解决相对会容易.
例3已知O为△ABC外接圆的圆心,外接圆的半径为1,且,若∠ABC=60°,则λ+μ的最大值为________.
解析
这道题的元素比较多,题目条件中给出了一个向量表达式,可以通过建立平面直角坐标系,将含向量的方程转化为代数方程,进而求解.
以O为坐标原点,建立平面直角坐标系,如图5所示,因为∠ABC=60°,所以∠AOC=120°.设B(x,y),则

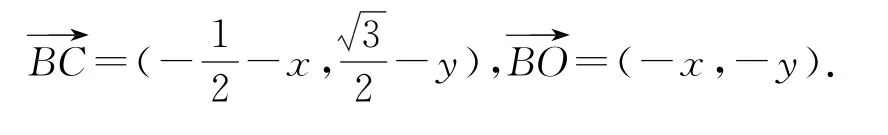

图5

因为点B在圆x2+y2=1上,所以化简得λμ=,因为点B在优弧上,所以时,取得等号).
点评
例3是用坐标法进行求解,利用点(x,y)的坐标在圆上构建含有λ,μ的式子,再通过基本不等式将问题解决.向量的坐标联系了向量与其他知识,可以借助其他知识处理问题的方法来解决向量问题,其中体现了转化与化归思想.
例4在△ABC中,AB=2,AC=3.若AE是△ABC的内角平分线,求AE的取值范围.
解析
此题是解三角形问题,根据向量的基底思想,用向量的方法加以处理,也会发现别有洞天(此处略去应用几何法以及应用正、余弦定理解决该题的方法).
依题分析,AE平分∠BAC,作菱形AFGC,使得AF=AC=3(如图6),则所以
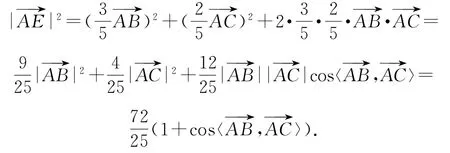
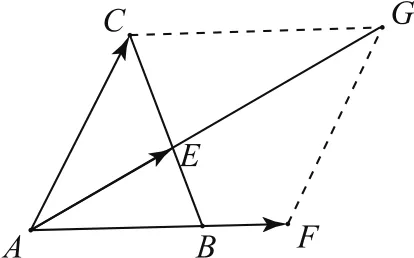
图6
点评
这道题用向量的方法巧妙地加以解决,比用几何法添加辅助线更容易上手,向量法解决几何问题的优势也就体现出来了.也可以将向量法与平面几何知识结合,利用三点共线时,向量的特点来处理.如图7所示,以AE为角平分线作平行四边形AMEN,设,因为B,E,C三点共线,所以

因为AE是∠BAC的角平分线,则|AM|=|AN|,所以,所以


图7
总之,向量是联系几何与代数的桥梁,向量有自己独特的处理问题的方式,蕴含着重要的思想,它又与其他知识有着密切的联系,用它解决平面几何、解三角形等问题会很简捷.通过坐标转化可以将向量问题变为代数问题,从而将向量问题很好地解决.
链接练习
1.A,B,C是圆 上不同的三点,线段CO与线段AB交于点D(点O与点D不重合),若R),则λ+μ的取值范围是________.
3.已知菱形ABCD的边长为2,∠ABC=60°,点E,F分别在边AB,DC上,则.

图8
链接练习参考答案