微电网储能电池寿命衰减模型研究
陈景文, 周光荣, 莫瑞瑞
(陕西科技大学 电气与控制工程学院, 陕西 西安 710021)
0 引言
以电池储能为主的储能系统是保证微电网稳定运行、推动可再生能源微电网技术广泛应用的关键技术手段[1,2].电池储能系统运行规划的关键因素之一是基于电池寿命的运营成本研究[3].储能电池工作在不断变化的运行条件(温度、放电深度、放电倍率)下,电池能量损失严重、利用率低、寿命急剧衰减,使得电池往往在其使用寿命结束前就已失效[4].因此基于电池寿命衰减的数学建模对于考虑更符合实际的储能运行成本至关重要.
电池衰减模型可分为机理模型和经验模型.机理衰减研究[5-7]多考虑电池详细的衰减机理,实现较为复杂,因此经验模型更适用于电池的寿命预估研究[8-14].文献[8]基于充电/放电循环次数的模型估计电池寿命;文献[9]考虑了放电深度对电池寿命的影响;文献[10]归纳基于交换功率的电池寿命模型.
单因素模型较为简单,实际应用中会产生较大误差[8-10].较为主流的是考虑多影响因素的电池衰减建模[11-13]:文献[11]建立了多因素聚合的累计电量寿命模型以延长电池储能系统使用寿命,反映放电倍率、循环次数和温度等因素对电池老化的影响;文献[12]通过筛选出影响容量衰减速率的四种主要应力,根据电池老化机理,提出Arrhenius形式的经验模型,有助于理解不同应力对电池老化的影响;文献[13]提出一种考虑电池荷电状态使用区间和充电倍率的锂离子电池使用方法.
上述多因素衰减模型多是基于或包含放电倍率而建立的,可在模型所述的运行条件下对电池寿命的衰减预估实现一定的准确度,但是以储能为控制核心的微电网在工作过程中为达到稳定运行效果,放电倍率具有较强的随机性,以该影响因素建立的寿命模型将不适合微电网系统分析研究.
基于此,文章提出一种用于储能电池寿命估算的衰减模型.对储能电池寿命特性进行分析,确定影响电池寿命的主要因素,在此基础上建立电池日历、老化模型再结合衰减特性和SEI形成建模完善模型.该模型可根据电池的运行情况如温度、放电深度、荷电状态和运行时间对电池寿命损失进行评估.电池循环测试和与现有模型的对比实验验证了模型的有效性和适用性.
1 储能电池寿命特性
微电网中储能电池在其使用过程中不可避免的会发生容量、功率衰减,内阻增加,进而导致电池寿命的衰减,其中影响电池寿命因素较多,包括充放电倍率、放电深度、温度、充放电截止电压等[14].为更准确的把握储能容量和电池模型,需要对电池寿命衰减特性进行分析.
1.1 温度对储能电池寿命的影响
温度对储能电池容量即寿命的衰减贡献较大,经典的Arrhenius方程常用于温度影响因素对电池容量衰减过程的定量描述:
(1)
式(1)中:k为化学反应的速率,此处可表示为容量衰减率;A为指前因子;Ea为活化能,单位J/mol;R为摩尔气体常数,其值为8.314;T为绝对温度,单位K.
由式(1)可以得到,电池温度的高、低都会很大程度上加快电池容量衰减.图1为某型号锂电池的温度与放电容量的关系曲线,其中电池标称电压3.2 V,容量2.23 Ah,在电流为1 A条件下进行放电测试.
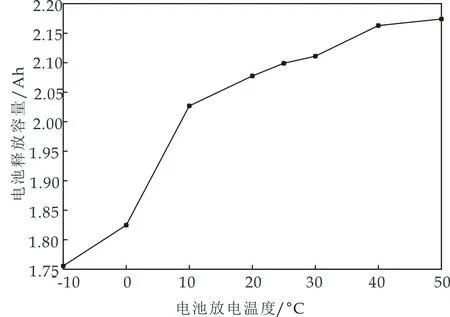
图1 温度对电池放电容量的影响
由图1可知,温度对锂离子电池容量的影响程度较为显著,在温度较低时电池释放容量相对较少,随着温度提高电池释放的容量逐渐增加.一般认为,20 ℃~40 ℃是电池工作特性发挥较好的温度区间.
1.2 放电倍率对储能电池寿命的影响
电池的放电倍率(C)是指电池在规定的时间放出其额定容量所输出的电流值,是储能电池循环过程中重要的影响因素,其作为一种电应力对电池寿命衰减具有加速作用.图2为某型号锂电池放电倍率与放电容量的实验关系曲线,电压3.2 V,电池容量1.1 Ah,放电温度25 ℃.由图2可知随着放电倍率的不断增大,加快电池容量的衰减,随着充放电次数的增加电池容量逐渐降低,直至达到完全衰减.但是实际的微电网中储能放电倍率受系统运行影响具有较强的随机性,使得利用其预测电池寿命较为困难,因此文章将放电倍率对储能的影响折合在储能荷电状态和放电深度之中,以实现对电池寿命的预估.

图2 放电倍率与放电容量的关系
1.3 放电深度对储能电池寿命的影响
放电深度(DOD)表示电池放电容量与额定容量的比值(百分比),较小的DOD可有效延长电池的寿命.图3为DOD对电池寿命影响实验结果,其中电池电压4.2 V,容量1.5 Ah,温度25 ℃.

(a)不同DOD条件下的放电曲线
由图3可以看到,不同DOD下电池容量衰减的速率明显不同,当电池以100%DOD放电时,电池衰减速率将达到最大,在放电深度不变时,随着循环放电的进行,电池容量将会逐步降低.
2 电池寿命衰减建模
电池的寿命衰减不仅取决于外部应力因素,如放电深度、荷电状态和温度等,还取决于其当前的寿命状态.因此,电池衰减是时间和应力循环的非线性过程,电池寿命的损失是所有日历和循环累积的结果.基于上述因素考虑电池老化和SEI机理建立电池寿命衰减模型.
2.1 电池日历和循环老化模型
电池老化包括日历老化和循环老化[15].其中日历老化反映了电池随时间t的衰减
(2)

循环老化是电池循环时损失的寿命,可用式(3)表示:
(3)
式(3)中:ξcyc为循环寿命损失;N为循环次数,ni为结合循环计数法所得的周期;δi为放电深度.
电池老化表示T、σ、δ、t的函数:
(4)
当N=0时,即电池未运行时,电池老化仅包括日历老化,Qloss可以改写成单位时间衰减的寿命线性表达:
(5)
当电池运行由相同DOD和平均SOC的循环组成时,可将老化模型转换为函数:
Qloss,cyc(T,σ,δ,t,N)=N(μt(T,σ,t)+μc(T,σ,δ))
(6)
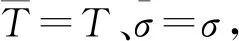
Qloss,cyc(T,σ,δ,t,N)=NQloss,cyc(T,σ,δ,t,1)
(7)
式(7)中:NQloss,cyc(t,δ,σ,Tb,1)记为Qloss,1,表示一次循环中得到寿命损失.
2.2 SEI的形成建模
日历和循环老化模型表明,只要运行条件(温度、SOC、DOD)相同,电池寿命衰减速率就相同,但相对于循环次数,储能电池的衰减速率并不是线性过程,如图4所示.将实际的每周期衰减率(dLb/dN)表示为Lb和一个周期内的线性衰减率的函数:
(8)
式(8)中:Lb为电池当前的寿命状态,通过电池损失的容量与额定容量的比值来实现归一化,即当Lb=0表示新电池;电池寿命终止通常定义为电池仅提供其额定最大容量的80%的点,即Lb=0.2.

图4 电池衰减行为曲线
由于衰减率与电池中剩余的活性锂离子数成正比,可用下面的公式表示:
(9)
将式(7)和式(8)合并,并对于Lb积分,可得电池寿命:
Lb=1-e-∑NQloss,cyc(T,σ,δ,t,1)=1-e-Qloss
(10)
电池寿命在早期快速衰减的特性可能是由各种机制引起的,但主要原因与固体电解质界面膜的形成有关.当新电池开始工作时,会消耗一定量的活性正离子来形成这种薄膜[16].当形成稳定的薄膜时,形成该薄膜的速率将会降低.所以电池活性材料的某一部分在瞬态阶段被消耗以形成此薄膜.形成速率与已形成的薄膜成反比,并且当形成稳定的膜时(稳态阶段)停止.
设ρs为SEI膜形成期间不可逆地消耗的电荷容量的一部分.其余部分以与电池寿命成比例的速率衰减(1-ρs).由此式(10)进一步改写成:
Lb=1-ρse-Qs-(1-ρs)e-Qloss
(11)
式(11)中:ρs的值范围为3%至8%,假设Qs与Qloss成正比:
Qs=φsQloss
(12)
代入式(11)得:
Lb=1-ρse-φsQloss-(1-ρs)e-Qloss
(13)
式(13)所示SEI模型仅包括SEI形成阶段,未考虑极端条件下SEI的破裂情况,可通过控制运行条件如温度、电流等使之稳定而不出现SEI膜的破碎现象,并且该模型适用于Lb=0的新电池,用于评估整个电池寿命的规划研究.若要将公式应用于废旧电池,因为其SEI膜的形成阶段已结束,建模过程中应忽略,此时仅需获得当前的电池寿命Lb′,从而利用式(14)计算电池寿命.
Lb=1-(1-Lb′)e-Qloss
(14)
2.3 模型评估和参数
对方程式(13)进行重写,以将薄膜模型应用于循环寿命衰减:
Lb=1-ρse-NφsQloss,1-(1-ρs)e-Qloss,1
(15)
使用拟合算法将等式(15)中的ρs,φs和Qloss,1的值拟合到实验性衰减数据,如图5所示.从而得到SEI模型参数ρs=0.05,φs=100.
式(15)求解需要首先确定Qloss,1,因此将式(2)、(3)中电池老化表示为由温度模型M(T)、时间模型M(t)、DOD模型M(δ)和SOC模型M(σ)等模型的组合,如式(16)所示:
μc(T,σ,δ)=M(T)M(σ,δ)
μt(T,σ,δ)=M(T)M(σ,t)
(16)
式(16)中:M(σ,δ)和M(σ,t)是两因素混合模型,可由各单因素模型的乘积得到,则式(7)可改写为:
Qloss,1=M(T)[M(δ)+M(t)]M(σ)
(17)
其中各单因素模型的具体表达式为:
(18)
式(18)中:温度模型基于Arrhenius公式的改进形式,c0为模型系数;Tref为参考温度,单位为K,值为293K;SOC模型为幂指函数,c1为模型系数,σref为SOC参考值,值为0.5;在消除了寿命依赖和其他因素之后,时间模型为时间的线性函数,c2为模型系数;DOD模型为类似于二次模型的改进形式,c3、c4、c5为模型系数.利用电池衰减数据可计算各模型参数.
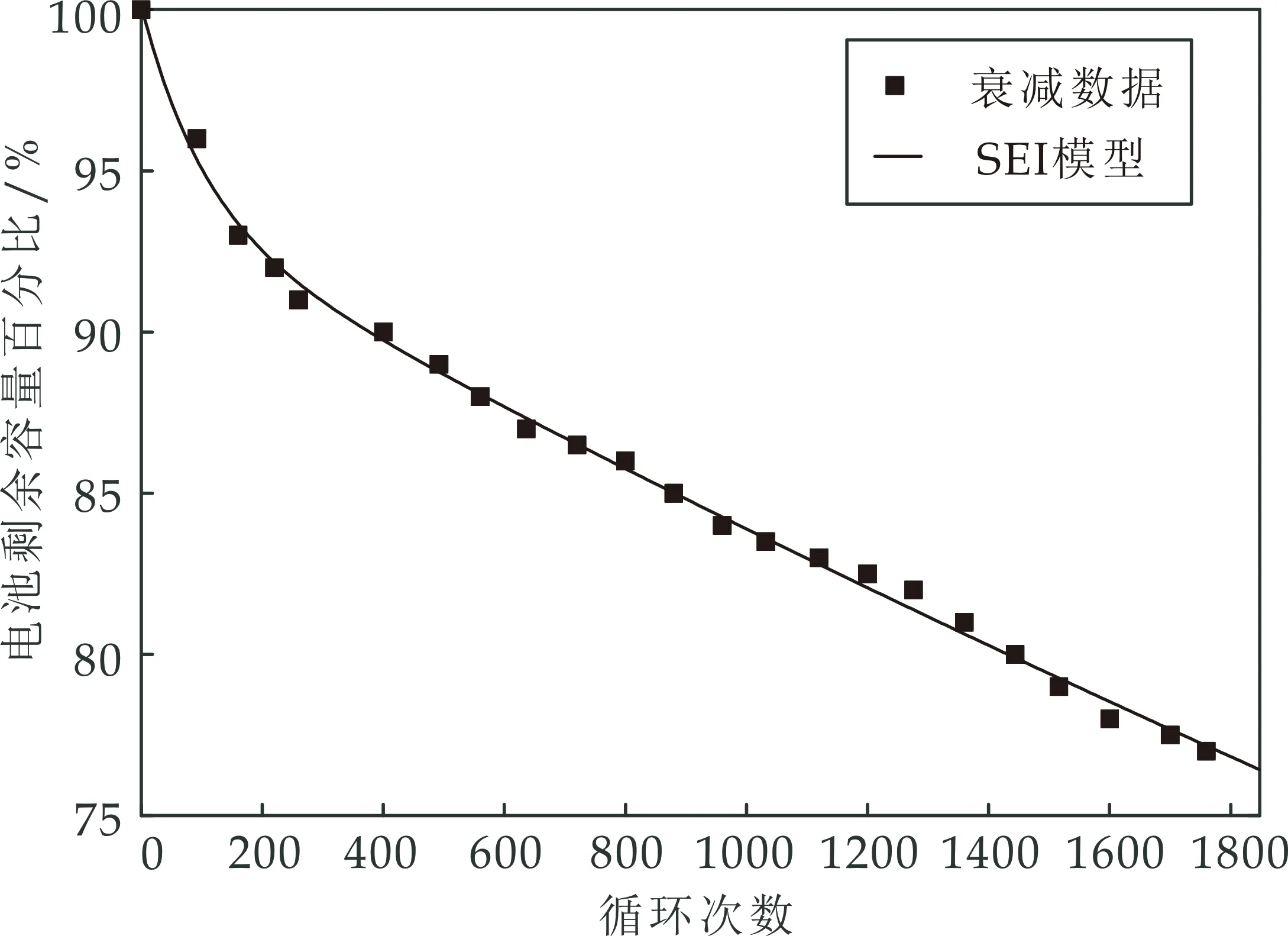
图5 衰减数据和SEI模型的拟合
3 模型验证
由上文所得为电池在不同T、DOD以及SOC条件下的循环寿命模型,利用电池制造商提供的衰减数据(Sony/Murata US26650FTC1 26650 磷酸铁锂/石墨(LFP/C)电池,标称容量为2.85 Ah电压3.2 V)可得式(18)所示的电池单因素模型的各模型系数为:c0=0.08,c1=1.02,c2=3.2E-10,c3、c4、c5的值分别为1.4E5、-0.5、-1.23E5.
利用上述模型参数对不同运行条件下的寿命(容量)衰减进行研究,采用来自A123系统的商用26650圆柱形LFP/C电池,标称电压3.2 V,额定容量为2.2 Ah.循环测试剩余容量与循环次数的实验数据及其模型拟合如图6所示.
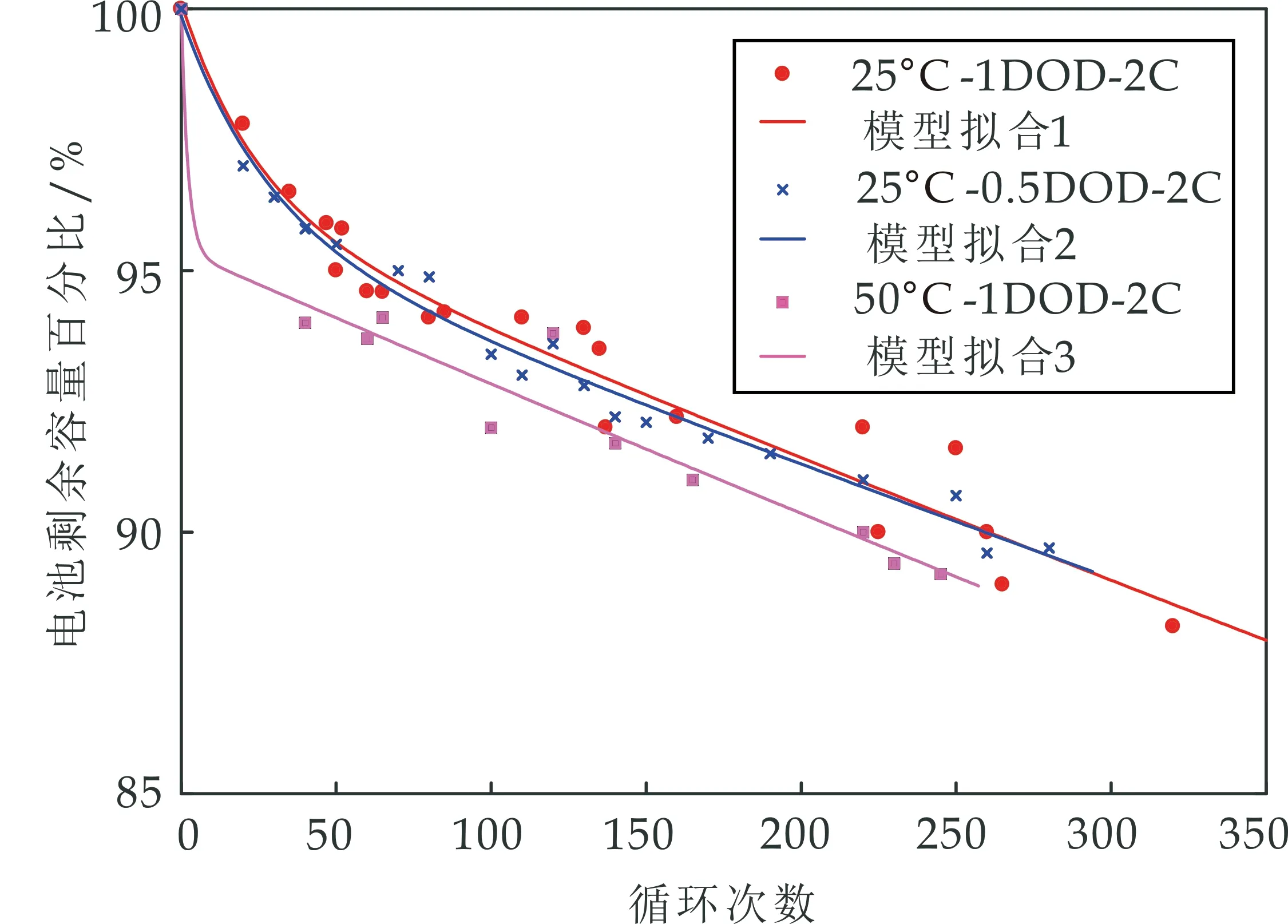
图6 不同运行条件下的循环测试与模型拟合
由图6可知,实线部分为各测试数据的模型拟合,以温度为25 ℃、100%DOD、2C放电倍率情况下得衰减测试为例,验证模型的拟合程度和对电池容量衰减的预估精度.其中,模型对测试数据的拟合程度用相关系数R2表示,其值控制在0~1之间确保模型对数据不会出现过拟合或欠拟合得情况,得到R2分别为0.998 0、0.99、0.992 0;循环200次时电池的容量剩余容量作为参考(即实验值)为92.1%,模型预测值为93.3%,进而可得预测误差为1.3%.
为验证模型的适用性,将提出的寿命衰减模型和现有模型进行对比分析.图7为提出的模型和现有锂电池寿命衰减模型对比,其中,对比的寿命衰减模型为基于Ah吞吐量模型的改进形式(Qfade=Aexp(B+Cx)/RT)·sqrt(N·DOD·QE),x为放电倍率,QE为额定容量,A、B、C为系数).由图7可知,该模型模型整体满足现有锂电池寿命衰减趋势,目前锂电池寿命衰减研究也大多将电池放电倍率考虑在内,出现分区间模型,相比而言,建立的寿命模型和目前衰减模型相比,除在起始阶段有较小偏差外,整体契合度较好.
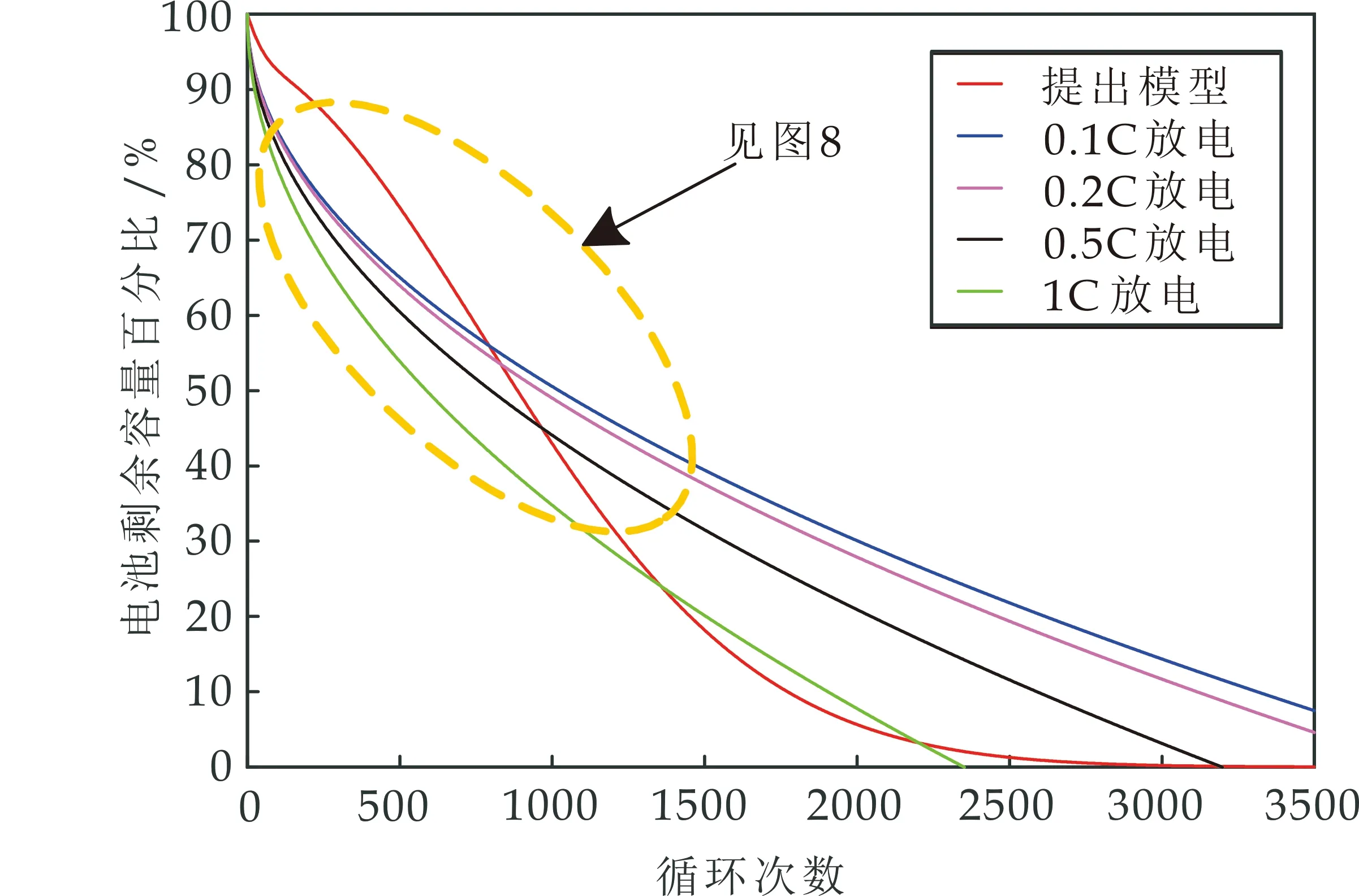
图7 锂离子电池寿命模型对比
进一步,本文将锂电池前600次循环和美国国家航天局(NASA)的锂电池测试数据(采用商用的18650 LFP/C锂离子电池,额定容量为2 Ah;NASA埃姆斯中心开展的较长时间加速寿命实验中B18号电池的衰减数据)进行对比,如图8所示.其中,从衰减测试数据拟合的拟合曲线(R2=0.999 2)和本文提出模型提供的衰减曲线(R2=0.999 4)具有较好的一致性.
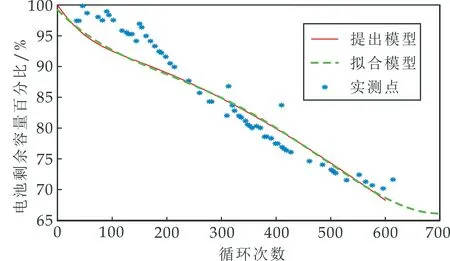
图8 提出的模型和NASA锂电池测试数据对比
在摒弃放电倍率对储能电池寿命影响建立了电池寿命衰减模型,根据不同的电池测试数据调整模型的参数,适用于其他电池储能系统,可较好的反映微电网中电池寿命衰减的实际情况,准确的预测储能电池的寿命.
4 结论
针对现有的电池寿命模型考虑放电倍率而不适合微电网储能研究使用的问题,将放电倍率对储能的影响折合在储能荷电状态和放电深度中,并考虑电池老化作用和SEI机理提出了用于储能电池寿命估算的衰减模型.将提出的寿命模型和现有电池寿命模型进行对比测试分析,结果表明,提出的模型整体可以满足现有锂电池寿命衰减趋势,对衰减数据的拟合程度较好并且对电池容衰减的预估误差为1.3%.实现了较高的预估精度.在摒弃放电倍率对储能电池寿命影响后模型可以较好的反映微电网中电池寿命衰减的实际情况,准确地预估储能电池的寿命.

