倍率控制下的机器人轨迹生成算法
游 玮 詹庆荣 方 明,
(1.埃夫特智能装备股份有限公司,安徽 芜湖 241007;2.安徽工程大学,安徽 芜湖 241000)
0 引言
机器人在完成轨迹规划后开始运动,在运动过程中有时需要动态调整机器人的运动速度,甚至还会临时停止或启动机器人,使机器人的运行速度出现过渡不平滑的现象[1]。此时,机器人不仅需要尽快响应用户的指令,而且还需要确保机器人在运动过程中始终沿着编程路径运动,且各轴的加速度以及加加速度不能超出其允许的极限值。如果单独设计各个轴(例如关节轴或坐标轴)的调速方法,那么不仅计算复杂,而且很难保证合成之后仍然沿着编程路径运行[2]。针对上述问题,常见的解决方法是笛卡尔空间轨迹规化和关节空间轨迹规划[3]。许多学者通过优化轨迹的拐点使轨迹过渡得更加圆滑,从而达到减少机器人频繁启停的目的,但会降低轨迹的跟随精度。该文通过引入倍率控制,在机器人动态调整运动速度的过程中,对倍率值变化速度进行规划。通过校验倍率值变化的速度和加速度,实时修改倍率值的上限值、下限值,从而对带有轨迹混成的运动轨迹进行规划。再对1段典型混合轨迹进行仿真实验,结果表明,该算法不仅可以提高机器人的路径跟随性能,而且还可以实现停止、启动、调速以及反向等功能。
1 倍率控制简介
机器人的倍率值(DYN)是指机器人实际运行速度与最大运行速度的百分比,当倍率为100%时,机器人将全速运行;当倍率为50%时,机器人应按照最大速度的1/2 来运行。为了使机器人在动态调整速度的过程中还能保证机器人可以沿着规划好的路径运动,需要将这种多维空间的动态调速问题转变为一维空间的动态调速问题,这样既可以简化计算,又可以保证调整过程中路径的跟随性。
路径的长度s是一维空间变量,对s的轨迹曲线进行调整可以保证路径的跟随性。但是这种调速方式也有3 个缺点:1) 需要确定s的速度、加速度以及加加速度限制条件。因为机器人不仅要满足该限制条件,而且还要满足关节端的限制条件,所以需要在调整过程中不停地校核关节端的约束条件,计算过程较为复杂。而且基于该方式进行调整,如果对s的速度等限制条件设置得过于保守,则调速过程太慢;如果设置得过于激进,则可能会出现关节端超出限制条件的情况,需要不断对其进行修正。2) 在采用该方式的情况下,无法确定调速结束时s的位置。3) 该方式在调速临近结束时的衔接计算较复杂。因为当前时刻与下一时刻s的速度、加速度等一般均不为0,所以为了保证速度和加速度的连续性,至少需要构造1 个四次曲线。
由于基于路径长度s的调速存在上述缺点,因此,该文通过推导与测试,提出了基于倍率r的调速方法,整个算法的框架如图1 所示,这种方式不仅能够使机器人在不同速度下恒速运动,而且还能够实现停止、启动、调速以及反向等功能。

图1 轨迹生成
2 倍率轨迹生成算法
2.1 时间重新参数化
无论是关节空间的运动还是笛卡尔空间内的运动,在完成机器人轨迹规划后均可以得到各关节位置随时间t的变化曲线。假设当前机器人某个轴倍率值为r(r∈[0,1]),则相当于这个时刻对位置变化方程中的t进行了参数化t'=rt,新的位置变化方程为θ(t')=θ(rt)。对其求取前三阶导数可得公式(1)~公式(3)。
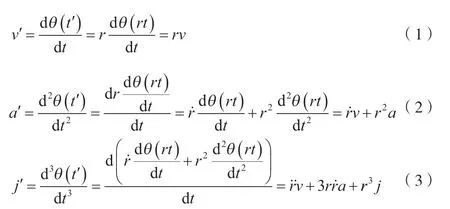
式中:v'为速度函数参数化;a'为加速度函数参数化;为倍率函数一阶导数;j'为加加速度函数参数化;为倍率函数二阶导数;j为加加速度;θ(t')为参数化后的位置变化方程;θ(rt)为对位置变化方程中的进行了参数化。
在实际运行过程中,倍率值一般会保持在某一定值,这个时刻新生成的轨迹相当于在时长上对全速时的轨迹进行等比放缩。当需要根据机器人关节运动速度变化实时调整倍率值时,新得到的轨迹与全速运行时的轨迹不再是等比例缩放的关系。
假设倍率的变化曲线是1 条关于时间的二次曲线,曲线方程如公式(4)所示。

式中:a、b和c为未知参数;t为时间。
为了便于分析,可以对公式(4)进行变形,使当前时刻所对应的t为0 s,从而得到公式(5)。

式中:r0为当前时刻所对应的倍率值分别为当前时刻倍率曲线的一阶导数、二阶导数。
假设当前时刻的位置对应全速轨迹中t0时刻的位置,则Ts时间后所对应的全速轨迹的时刻t1如公式(6)所示。
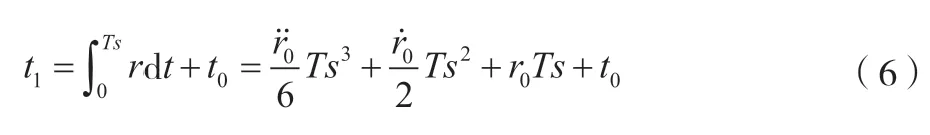
Ts时间后所对应的倍率及其一阶导数、二阶导数如公式(7)~公式(9)所示。

2.2 倍率速度规划
为了减小冲击,规划出的各轴运动曲线方程应该满足三阶连续性(即加速度连续)的要求。在使用倍率曲线对时间进行重新参数化后,根据复合函数的连续性准则可知:如果要保证新生成的各轴运动曲线的三阶连续性,那么时间参数化曲线也应该满足三阶连续性的要求,即应该保证倍率曲线(对时间参数化曲线求取一阶导数)的二阶连续性(速度连续)。
综上所述,倍率曲线只需要速度连续即可,加速度可以跳变。因此,可以按照梯形速度曲线对倍率曲线进行规划。梯形速度规划的关键参数为最大速度vimax以及允许的加速度和减速度aimax,而这些参数可以根据当前时刻各轴允许的最大速度和最大加速度jimax来确定。其限定条件如公式(10)~公式(12)所示。
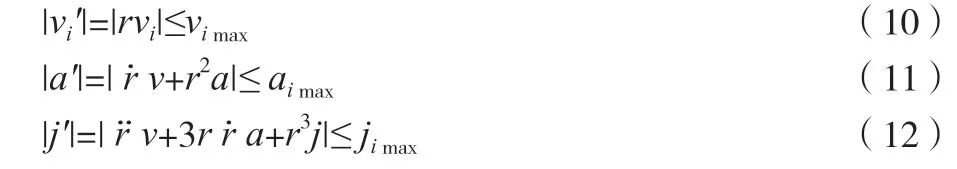
式中:vi为i时刻的速度;为i时刻速度的一阶导数;j为关节加速度;j'为关节加速度一阶导数。
假设目标倍率为rt,当前时刻的倍率、速度和加速度分别为rs、和,利用关节加加速度限制条件推导出当前时刻所允许的二阶导数的上限、下限分别为,下一时刻的倍率、速度和加速度分别为re、,利用关节加速度以及加加速度限制条件得到下一时刻所允许的速度和加速度的上限、下限分别为以及。然而下一时刻倍率的速度及其加速度限制条件还不够,还需要考虑以下2 点:1) 在该倍率速度下,如果按照最大减速度(或加速度)减速(或加速)至0 °/s2时,停止点的倍率是否会超出目标倍率值。2) 在倍率十分接近目标倍率的情况下,倍率的速度是否也接近于0。
针对第一点,可以根据梯形速度规划形式修正其速度的上限或下限,如公式(13)~公式(14)所示。
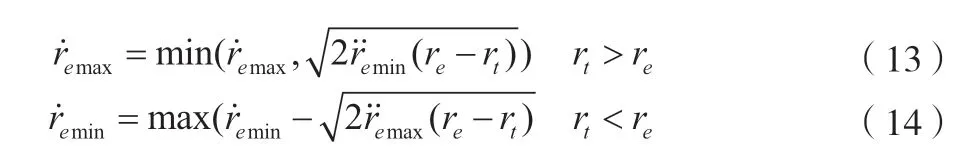
针对第二点,根据该时刻速度与目标速度的接近程度确定这一时刻各关节的加速度限制条件。假设当前倍率下某一关节的速度为vc、加速度为ac,那么在目标倍率下,该关节的速度为vt、加速度为at且调整时间为t,允许的最大加加速度为jmax,当前的加加速度为j。根据该约束准则可以得到公式(15)~公式(16)。

求解公式(15)~公式(16)可得公式(17)。

在公式(17)中,需要对ac和j的正负进行分析,分析不同情形下确定ac和j的正负号的准则。
当vt>vc>0 且at>0 时,当前的加速度ac可以大于at,加加速度应为-jmax,此时有公式(18)。

式中:tcmax为加速段最大时长。
反之,则有公式(19)。

当vt>vc>0 且at≤0 时,如果当前的加速度ac<0,则将加速度调整至目标加速度,速度不仅小于vt,而且还会小于vc。因此,此时的ac必须大于0,即ac的下限为0。ac的上限可以根据公式(20)来求解。

同理可以得出,当vt<vc<0 时加速度的上下限。对于倍率减小的情况,也可以按上述分析过程来确定当前加速度的上限、下限。假设该关节在当前位置下全速运行时的速度和加速度分别为v和a,则公式(21)~公式(23)成立。

式中:rc为tc时刻速度倍率值;vc为tc时刻的速度。
对上述分析进行汇总可以得出,当rc<rt时,有公式(24)~公式(25)。
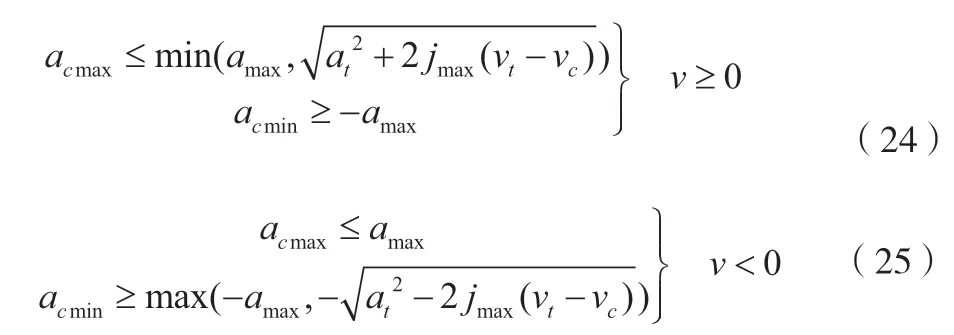
式中:acmax为tc时刻加速度的最大值;acmin为tc时刻加速度最小值;amax为加速度最大值。
而当rc>rt时,有公式(26)、公式(27)。
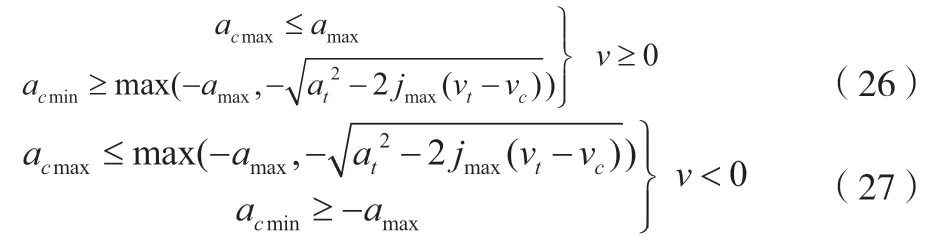
2.3 倍率加速度校核
为了进一步优化倍率速度,需要对倍率的加速度进行条件约束,其流程图如图2 所示。如果倍率的加速度满足约束条件,则直接进入倍率的速度校核部分。反之,如果倍率的加速度超出其上限,则应将倍率的加速度设置为上限。如果倍率的加速度超出其下限,则应将倍率的加速度设置为下限。

图2 加速度校核
首先,校核倍率速度是否超出了其上限、下限,如果没有,则校核结束,按照公式(28)~公式(31)更新倍率及时间参数。

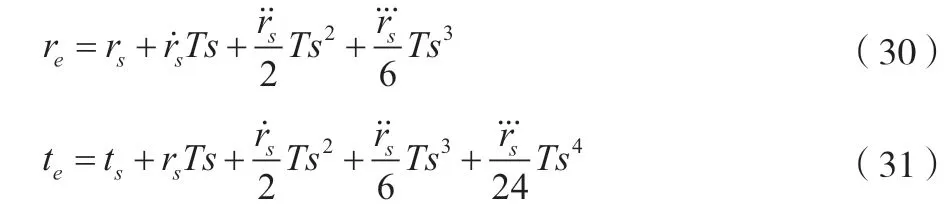
如果倍率速度超出了其上限、下限,则应修改倍率加速度,使倍率速度能够满足限制条件。从图2 中可以看出,这部分的流程是对称的,左侧是倍率速度过大的情况,右侧是倍率速度过小的情况(两侧的处理思路是一致的),这里选择左侧倍率速度过大的情况进行分析。
如果当前时刻和下一时刻的倍率加速度均为其下限,说明已经使用了最大的减速能力,此时就无法再调整倍率加速度,直接进入更新参数环节。反之,将下一时刻的倍率速度设置为其倍率速度上限。然后根据公式(32)求解下一时刻的倍率加速度。

如果新求出的下一时刻的倍率加速度大于或等于其下限,就说明能够满足加速度约束,直接进入参数更新环节;反之,则令下一时刻的倍率加速度为其下限,然后按公式(33)反算当前时刻的倍率加速度。如果其满足当前时刻倍率加速度的上限、下限,则直接进入参数更新环节;反之,则令当前时刻的倍率加速度为其下限,然后再进入参数更新环节。

在完成下一时刻的倍率速度及加速度校核和调整任务后,就可以根据调整后的倍率及其一阶导数、二阶导数计算下一时刻的位置、速度、加速度以及加加速度并输出相关数据。最后,将下一时刻的倍率、倍率速度和时间设置成当前时刻的值就可以生成单个周期的在线轨迹。
3 轨迹生成仿真实验
由上述分析可知,整个倍率控制下的轨迹规划核心在于通过规划1 条一阶连续的倍率曲线来调整倍率值,进而调整机器人的运动轨迹。下面将以1 条带有轨迹混成的3 段PTP 运动为参考轨迹,通过MATLAB 机器人工具箱仿真得到的轨迹,如图3 所示。
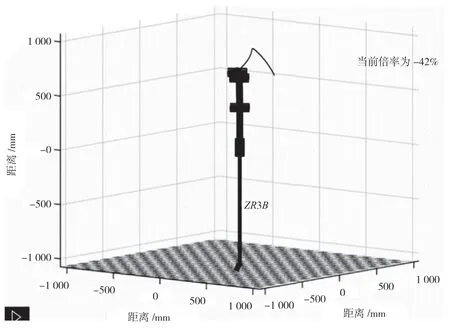
图3 混成轨迹
该轨迹主要分为3 段:第一段为全速运行,机器人达到最大速度后继续运动一段距离。第二段为变倍率运行,在运动过程中不断改变机器人的运动速度。第三段沿着原有轨迹反向运动。图4 为机器人全速运行时的轨迹特定曲线位置-速度-加速度-加加速度图,为了使图像更加简洁、清晰,图4 中只展示机器人前3 个轴的运动曲线。
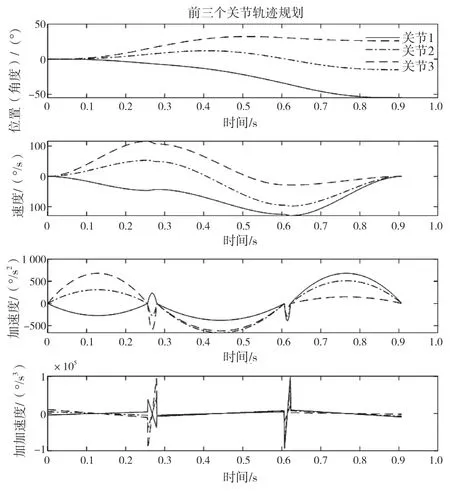
图4 全速运动部分规划结果
在机器人运行的过程中,可以在不同时刻通过调整倍率值来实现轨迹的动态调速、停止、启动以及反向运动等功能,最终的效果如图5 所示。图5 中共有8 条竖虚线,点虚线是倍率开始调整的时刻,虚线是倍率调整结束的时刻。从左往右看,第一条点虚线所处时刻,机器人的倍率开始从50%增至100%。第二条点虚线所处的时刻,机器人响应停止的指令,开始减速,直至速度为0 °/s。机器人停了约0.18 s 后,即第三条点虚线所处的时刻,启动机器人,机器人开始加速直至达到全速状态。在第四条虚线所处的时刻,机器人响应反向运动的指令,开始将速度降低,直至可以反向全速运动。
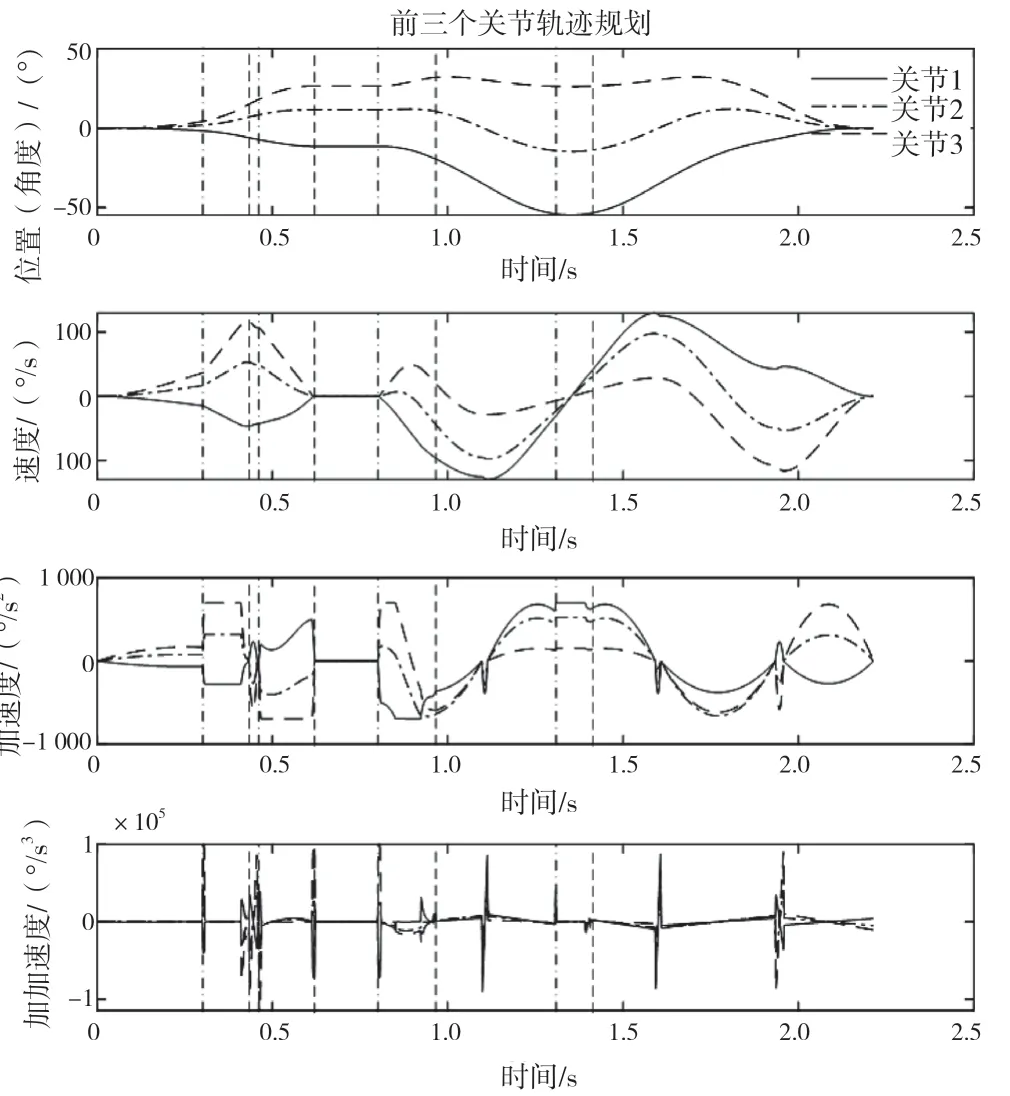
图5 倍率调整轨迹图
由图5 可以看出,生成的位置-速度曲线光滑且连续,加速度和加加速度都在允许的范围内。机器人在动态调速过程中没有产生明显的振动,在变速过程中提高了稳定性以及机器人的路径跟随性能。
图6 为整个调整过程中倍率值的变化曲线。通过检测相关数据可以发现,倍率超调的现象仅在机器人关节运动停止的过程中出现(倍率降为-3.4×10-6),且这种超调很小,完全可以忽略不计。
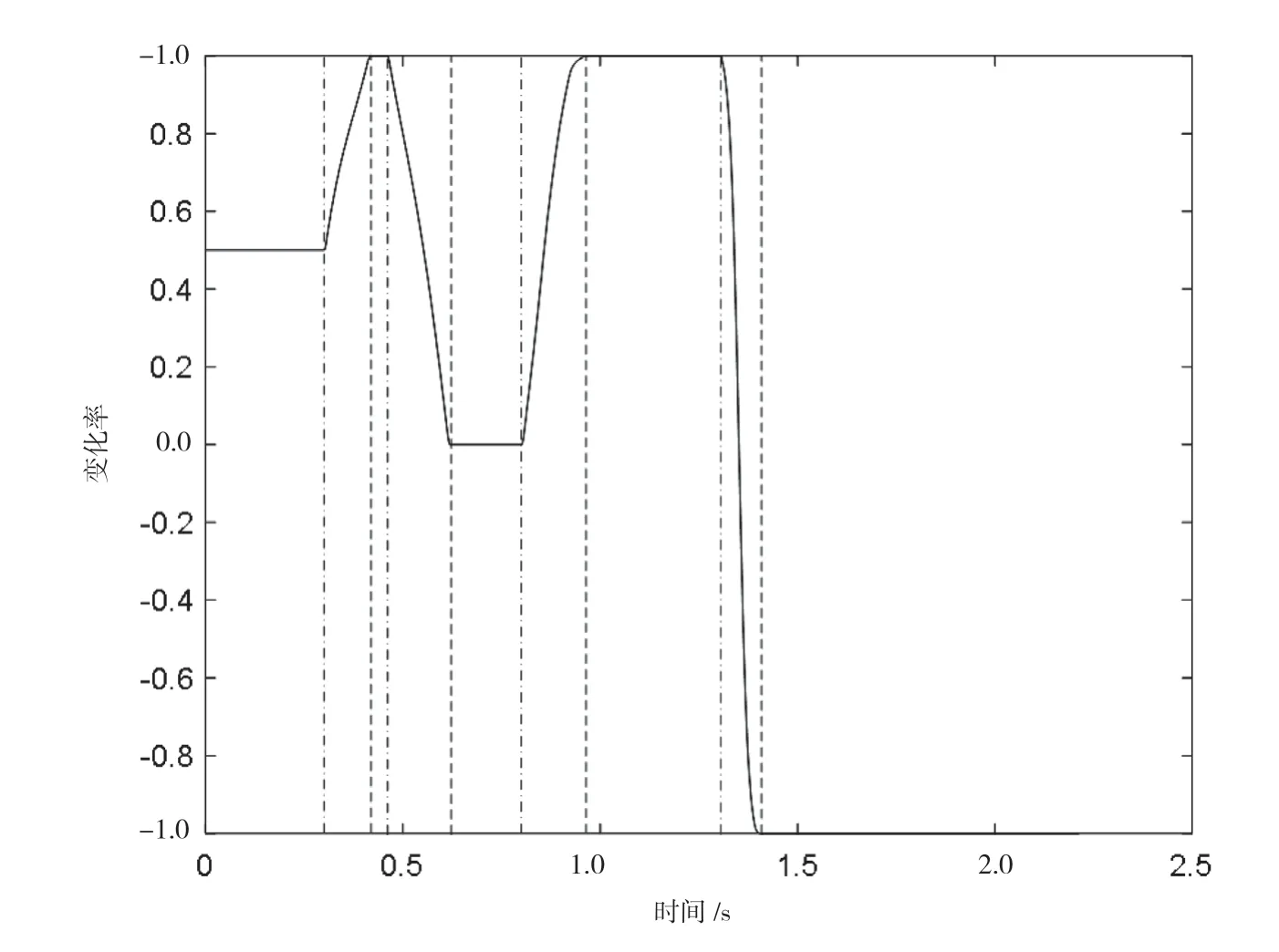
图6 倍率变化
图7 和图8 分别展示了倍率的速度和加速度变化曲线,从这2 幅图中可以看出,不同位置处所允许的倍率速度和加速度相差较大、倍率曲线速度连续且加速度跳变,满足预期设计的梯形速度规划。

图7 倍率的速度图
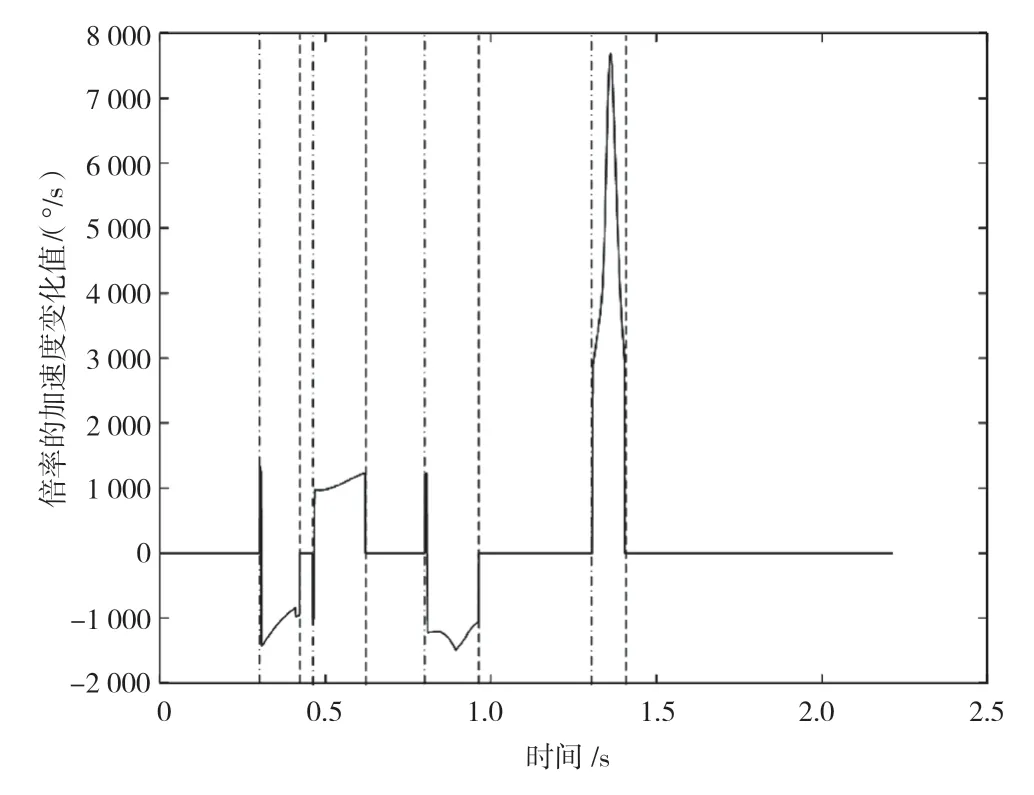
图8 倍率的加速度图
4 结论
倍率控制下的机器人轨迹生成算法有效地解决了机器人在运动过程中动态调整机器人运动的速度,会使机器人运动路径的跟随性下降,导致机器人出现运动轨迹精度下降的问题。该算法通过校核倍率曲线的速度规划和加速度来保证机器人运动轨迹跟随的准确性。通过仿真试验得到的轨迹位置和速度曲线图具有连续性,验证了该方法的可行性。结果表明,该方法有效解决了传统调速造成的频繁启停问题,既提高了机器人运动时在实时调整速度过程中的路径跟随性能,又实现了停止、启动、调速以及反向等功能,提高了机器人的作业效率。

