施工期混凝土重复荷载作用下的受压应力-应变关系

彭 刚， 胡晓鹏,2， 牛荻涛,2， 王 静

(1.西安建筑科技大学 土木工程学院， 陕西 西安 710055；2.西安建筑科技大学 省部共建西部绿色建筑国家重点实验室， 陕西 西安 710055)

中国幅员辽阔、地震多发，加之基础设施建设正处于快速发展中，地震发生时很多混凝土结构尚处于施工阶段.相关统计数据表明[1]，汶川地震时，中国约有200多亿平方米的在建建筑物遭受了6度以上的地震作用.与正常使用阶段相比，施工阶段的混凝土结构具有混凝土性能时变、荷载效应复杂、受模板支撑体系作用明显和结构传力机制不成熟等特征[2].因此，施工期混凝土结构在遭受地震作用时的破坏程度和破坏特征会明显不同于正常使用阶段.

对施工期混凝土结构震损特征进行研究是客观评价施工期混凝土结构后续使用可靠性的基础.近年来，随着计算机技术的高速发展，数值模拟分析方法已成为研究施工期混凝土结构震损特征的重要手段，然而数值模拟分析方法的使用需要以材料的本构关系模型为基础.遭受地震作用的施工期混凝土结构处于重复受荷载的状态，因此，施工期混凝土重复荷载作用下的本构模型对施工期混凝土结构震损特征的研究起着至关重要的作用.

目前，部分学者基于单调加载试验，提出了施工期混凝土单调荷载作用下的受压应力-应变本构关系模型，为施工期混凝土结构的可靠性分析提供了一定的理论支撑[3-8].然而，尚未有施工期混凝土重复荷载作用下的受压应力-应变本构关系方面的研究.可靠的重复荷载下施工期混凝土本构关系计算模型的缺乏，给施工期混凝土结构震损特征的研究造成了一定的困难.

本文通过重复荷载作用下施工期混凝土的受压试验，分析了重复荷载作用下混凝土试件受压应力-应变全曲线的各特征参数(峰值应力、峰值应变、外包络线、卸载曲线和再加载曲线等)随混凝土龄期的变化规律，建立了重复荷载下施工期混凝土的受压应力-应变关系模型，为施工期混凝土结构震损特征研究提供可靠的支撑.

1 试验

1.1 原材料及配合比

水泥为P·O 42.5普通硅酸盐水泥，细度1)为0.6%，其主要性能指标见表1；细骨料为沣河河沙，细度模数为2.9，堆积密度为1450kg/m3；粗骨料为粒径5～20mm的碎石，堆积密度为1550kg/m3；高效减水剂为PCA®-I聚羧酸高性能减水剂，减水率在20%左右，1h内无坍落度损失.混凝土试件的配合比见表2.

表1 水泥的主要性能指标

表2 混凝土试件的配合比

1.2 试件设计及制作

混凝土强度等级为C30、C40和C50，龄期分别为8、16h以及1、3、7、28d.试件采用组合钢模具浇筑成型，尺寸为100mm×100mm×300mm，每组3个试件.对龄期小于1d的试件，标准养护至开始试验时拆模；对龄期大于等于1d的试件，标准养护 1d 后拆模，将其放置在标准养护室中养护至设定龄期.

1)文中涉及的细度、减水率等均为质量分数.

1.3 加载制度

用改进的WAW-1000系列微机控制电液伺服万能试验机对不同龄期的混凝土试件进行重复加、卸载试验，采用2个固定架以及位移计并借助TDS-602动态数据采集仪记录试件的荷载及轴向变形，位移计精度为0.01mm，固定架间距为200.00mm，试验装置示意图见图1.为了保证试件轴心受压，首先对试件进行预加载，加载至5kN时观察2个位移计读数是否相近，若相差过多则停止试验，重新进行对中.试验采用位移控制的方式进行等位移增量加载，每级加载位移增量为0.05mm.加载至预定应变值后卸载至荷载为零，加、卸载速率均为0.10mm/min，试件完全破坏时停止试验.

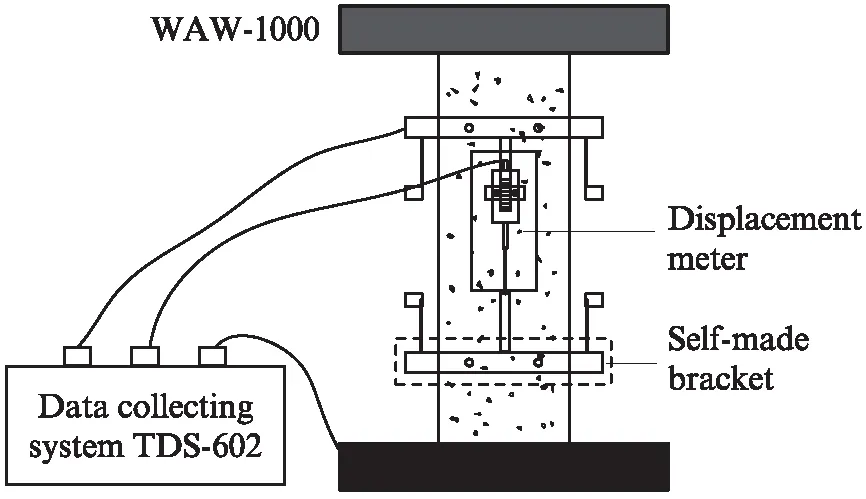
图1 试验装置示意图Fig.1 Schematic diagram of test equipment

2 结果与分析

2.1 试件破坏过程

图2以C30混凝土试件为例，给出了不同龄期混凝土试件的破坏形态.短龄期的试件破坏为浆体自身、浆体-粗骨料之间产生黏性错动，粗骨料无破坏，破坏面较为模糊；长龄期的试件破坏为浆体裂缝、浆体-粗骨料界面裂缝、个别粗骨料断裂裂缝的延伸所导致，破坏面较齐整.

图2 C30试件破坏形态Fig.2 Failure modes of C30 specimens

2.2 力学性能参数及其计算模型

表3为重复荷载作用下试件的力学性能参数.表3中：σ1,t、ε1,t、E0,t、Ep,t分别为龄期t时混凝土试件的峰值应力、峰值应变、初始割线模量、峰值点割线模量；E0,t取应力0.4σ1,t处对应的割线模量，Ep,t取峰值应力及峰值应变点处的割线模量；各性能参数采用3个试件测试值的算术平均值，3个测试值中的最大值或最小值中如与中间值的差值超过中间值的15%时，则取中间值.由表3可见：随龄期的延长，混凝土试件的峰值应力增加，峰值应变减小，初始割线模量、峰值点割线模量均有不同程度的增大；相比于初始割线模量，峰值点割线模量增长幅度相对较小.

表3 重复荷载作用下试件的力学性能特征参数

图3为重复荷载作用下混凝土试件的相对峰值应力σ1,t/σ1,28、相对峰值应变ε1,t/ε1,28随龄期的变化规律.由图3(a)可见：随着龄期的延长，混凝土试件的相对峰值应力呈指数型增大；随着混凝土强度的增大，相对峰值应力的增长速度增大.这一规律与早龄期混凝土抗压强度随龄期的时变规律基本一致[9-10].由图3(b)可见：随着混凝土龄期的延长，混凝土试件的峰值应变呈负指数型减小，1d内混凝土相对峰值应变急剧减小，1d后相对峰值应变减小速度明显减缓并逐渐趋于稳定；3种强度等级混凝土试件峰值应变随龄期延长而减小的幅度基本一致.分别对3种强度等级混凝土的相对峰值应力、相对峰值应变与龄期的对应关系进行拟合，得到如下的关系表达式[8]：

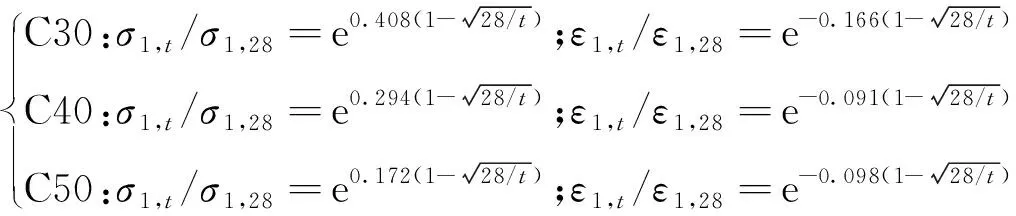
(1)

图3 重复荷载作用下混凝土试件的相对峰值应力、相对峰值应变随龄期的变化规律Fig.3 Variations of relative peak stress and relative peak strain of concrete specimens with age under repeated loading

2.3 受压应力-应变全曲线、外包络线及其计算模型

图4～6分别为重复荷载作用下C30、C40、C50混凝土试件的受压应力-应变(σ-ε)全曲线.由图4～6可见：重复荷载作用下不同龄期、混凝土强度等级的混凝土试件受压应力-应变全曲线的卸载曲线、再加载曲线均有明显不同.沿应力-应变全曲线外轮廓描线，可得其相应的外包络线，如图7所示.由图7可以看出：不同龄期混凝土的外包络线形状相似；随着混凝土龄期的延长，外包络线上升段及下降段均变得陡峭，峰值应力、初始割线模量及峰值点割线模量迅速增大，峰值应变逐渐减小，破坏特征逐渐显现出脆性破坏的特征；对龄期相同的混凝土试件，混凝土设计强度越高，其初始割线模量、峰值点割线模量及峰值应力越大，峰值应变越小，且混凝土试件的弹性模量随龄期增长的速度越快.这与单调受压作用下施工期混凝土应力-应变全曲线得到的结论基本一致[5-7].

混凝土重复荷载作用下的外包络线与单调加载的全曲线十分接近，通常采用单调加载全曲线表达式近似描述外包络线的曲线形态[11-13].采用式(2)的分段式曲线方程对不同龄期混凝土的外包络线进行拟合分析.

(2)

式中：x=ε/ε1，y=σ/σ1，σ1、ε1分别为峰值应力和峰值应变；ac和bc分别为外包络线曲线上升段和下降段参数，其值取决于混凝土的强度等级和龄期，其拟合结果见表4.

2.4 卸载曲线及其方程

由混凝土的受压应力-应变全曲线外包络线上的任一点(εu,σu)卸载至(εp,0)，得到完全卸载曲线.将卸载时的应变εu和残余应变εp分别除以峰值应变ε1，进行无量纲化处理，得到图8所示的混凝土卸载应变比(εu/ε1)-残余应变比(εp/ε1)的关系.由图8可见：卸载应变比相同时，混凝土的残余应变比随龄期延长逐渐减小.这是因为随着龄期延长，混凝土材料的“脆性”特征逐渐显现，混凝土变形恢复能力逐渐减弱.参照文献[13-14]的计算模型，对得到的卸载应变比εu/ε1与残余应变比εp/ε1关系进行拟合分析，结果如下式所示.

εp/ε1=a1(εu/ε1)b1

(3)

图4 重复荷载作用下C30混凝土试件的受压应力-应变全曲线Fig.4 Compressive stress-strain curves of C30 concrete specimens under repeated loading

图5 重复荷载作用下C40混凝土试件的受压应力-应变全曲线Fig.5 Compressive stress-strain curves of C40 concrete specimens under repeated loading

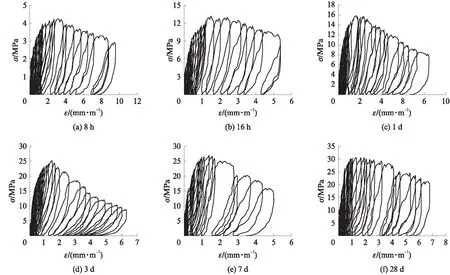
图6 重复荷载作用下C50混凝土试件的受压应力-应变全曲线Fig.6 Compressive stress-strain curves of C50 concrete specimens under repeated loading

图7 重复荷载作用下混凝土试件的外包络线Fig.7 Envelope of concrete specimens under repeated loading

表4 外包络线参数拟合结果

(4)

对试件的每次卸载过程(εu/ε1=0.0563～2.0243)，以修正卸载应变比(ε-εp)/(εu-εp)为横坐标、应力比σ/σu为纵坐标得到混凝土试件归一化后的卸载曲线.图9为龄期为8h的C30混凝土试件归一化后典型的卸载曲线.由图9可见：随着修正卸载应变比的增大，卸载曲线下凹程度逐渐增大.这说明随着加卸载次数的增加，混凝土内部损伤不断积累，卸载过程中应变恢复滞后现象越来越明显.

图8 卸载应变比-残余应变比的关系Fig.8 Relationship between unloading strain ratio and residual strain ratio

图9中归一化后的卸载曲线满足幂函数的形式：

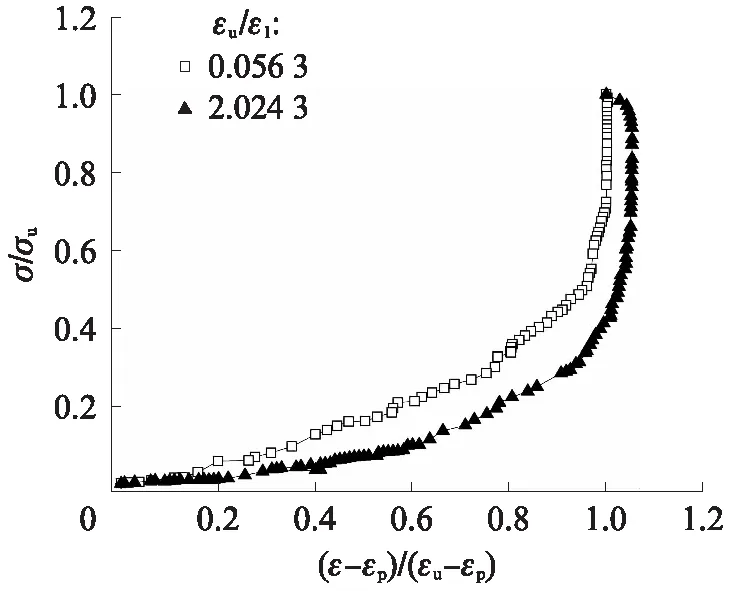
图9 龄期为8h的C30混凝土试件归一化后典型卸载曲线Fig.9 Typical unloading curves of C30 concrete specimens at 8h after normalized

(5)

式中：n为卸载参数.

参考文献[12]的公式：

n=1+k(εu/ε1)

(6)

结合式(5)和式(6)对各条卸载曲线分别进行拟合分析，得到了卸载参数n与卸载应变比εu/ε1的对应关系，如图10所示.由图10可见：随着龄期的延长、混凝土设计强度的提高，卸载参数n增大.这说明对同一卸载应变比的试件，龄期越长、混凝土设计强度越高，混凝土抵抗损伤积累的能力越强，卸载曲线下凹程度越缓，卸载曲线分布范围越大.对图10的结果进行拟合分析，得到系数k的表达式：

图10 卸载参数n与卸载应变比的关系Fig.10 Relationship between unloading parameter n and unloading strain ratio

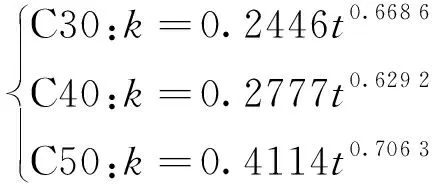
(7)

2.5 再加载曲线及其方程

从横坐标上(εp,0)开始加载，至与外包络线相切重合(εr,σr)，此段为再加载曲线.将再加载时的起始应变εp和终点应变εr除以峰值应变ε1，进行无量纲化处理，得到再加载曲线起始应变比εp/ε1与终点应变比εr/ε1的关系，如图11所示.由图11可见：在相同再加载起始应变比下，随着龄期的延长，混凝土抵抗损伤积累的能力增强，再加载曲线斜率逐渐减小，混凝土的终点应变比增大.对再加载曲线起始应变比εp/ε1与终点应变比εr/ε1的对应关系进行拟合，分析结果如下式所示.

εr/ε1=a2(εp/ε1)b2

(8)

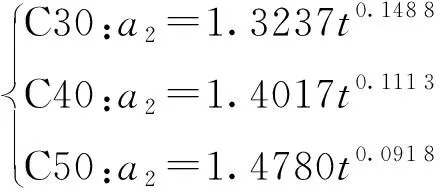
(9)

(10)

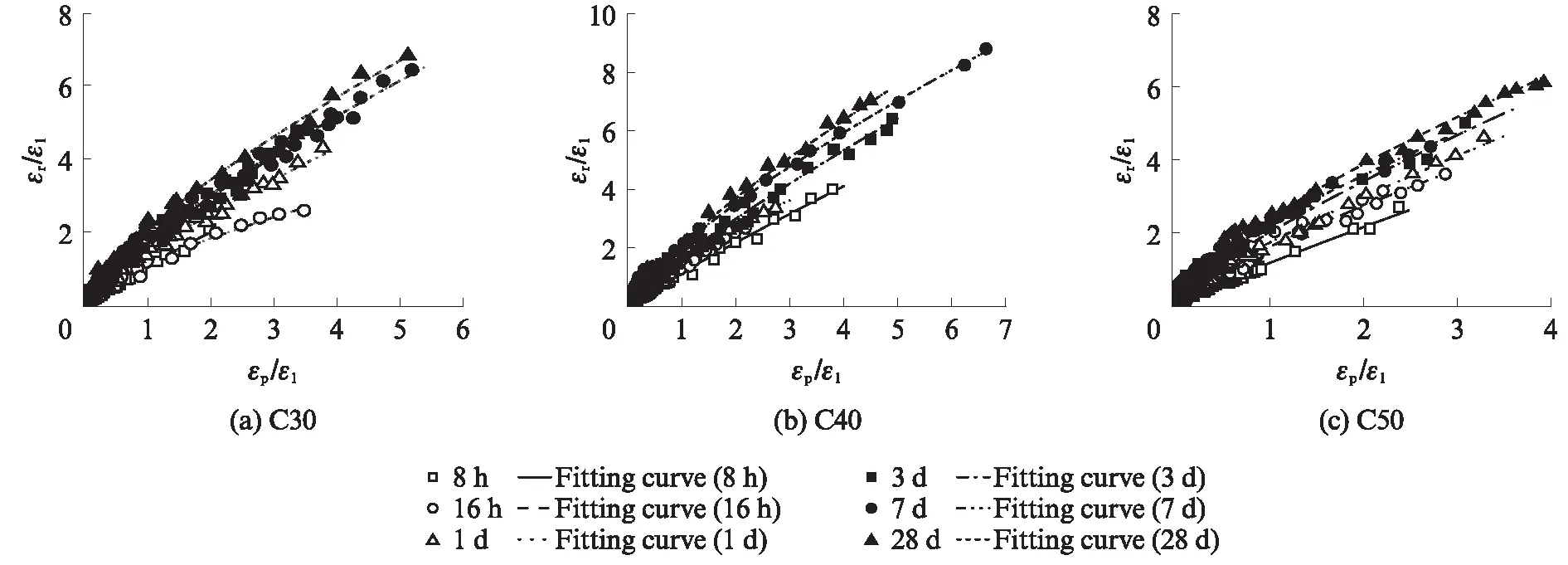
图11 再加载曲线起点应变比-终点应变比的关系Fig.11 Relationship between the starting strain ratio and the ending strain ratio of the reloading curves

对试件的再加载过程，以修正再加载应变比(ε-εp)/(εr-εp)为横坐标、应力比σ/σr为纵坐标，得到混凝土试件归一化后的再加载曲线.图12为龄期8h的C30混凝土试件归一化后的再加载曲线.由图12可见：施工期混凝土试件再加载曲线存在2种形状，当再加载曲线在全过程上升段(ε≤ε1)与外包络线上升段相切时，曲线斜率单调减小，至切点处曲线斜率仍大于零，曲线上无拐点；当再加载曲线在全过程下降段(ε>ε1)与外包络线下降段相切时，曲线斜率先增后减，曲线切点处斜率小于零，存在拐点.

基于文献[12-13]的计算模型，对修正再加载应变比(ε-εp)/(εr-εp)与应力比σ/σr的对应关系进行拟合分析，分析结果见下式：

(11)

式中：m、q分别为再加载曲线参数.

m、q可通过试验数据拟合确定，拟合结果见表5.由表5可见：再加载曲线参数m随着龄期的延长而增加，当龄期≥16h后再加载曲线参数q趋于定值.

图12 龄期8h的C30混凝土试件归一化后再加载曲线Fig.12 Normalized reloading curves of C30 concrete specimens at 8h

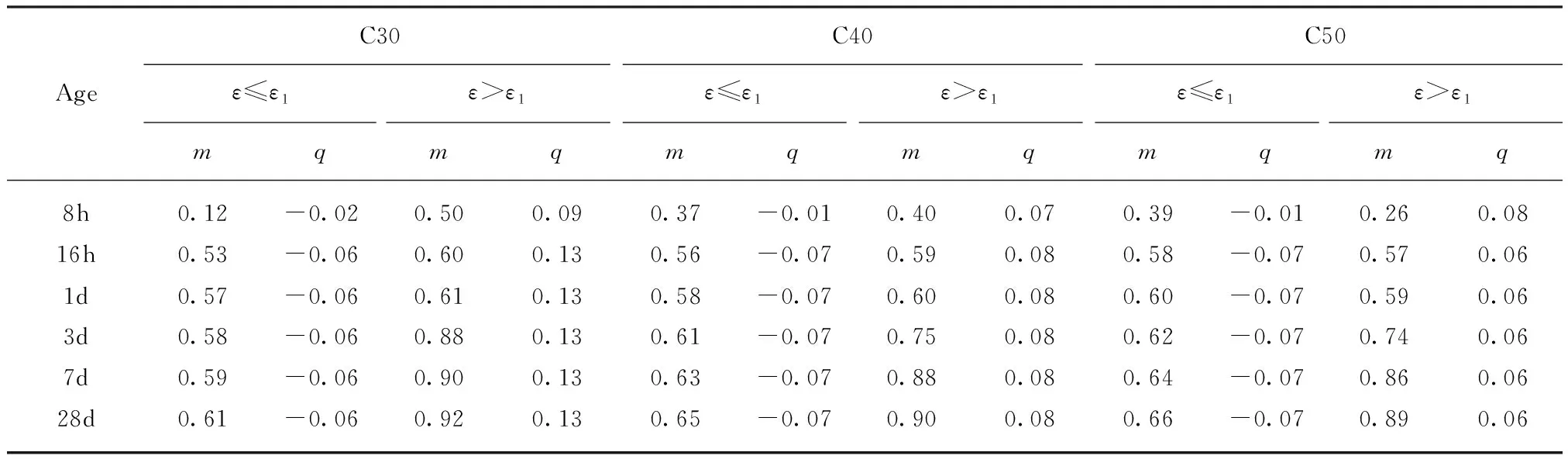
表5 再加载曲线参数m、q取值

3 结论

(1)随着龄期的延长，混凝土试件的弹性变形阶段延长，同一应力水平下试件的轴向变形减小，裂缝宽度、长度增长速度减缓，试件破坏越慢，破坏面越齐整.

(2)随龄期的延长，混凝土试件的峰值应力增大，峰值应变减小；初始割线模量、峰值点割线模量增大，但峰值点割线模量增长幅度相对较小；混凝土设计强度越大，峰值应力增加趋势越明显.

(3)随着龄期的延长，混凝土试件的外包络线上升段及下降段均变得陡峭，破坏特征逐渐显现出脆性破坏特征.