双渐开线齿轮参数对啮合刚度的影响

李海燕 方志远 许君君

(安徽粮食工程职业学院 机电工程系，安徽 合肥 230000)

刚度激励是一种最为主要的齿轮系统动态激励，是计算轮齿啮合时产生的弹性变形，以及相应的时变啮合刚度。也是齿轮传动系统动力学重点研究的内容之一。国内外学者做了广泛的研究：黄康[1]等人采用有限元法计算了斜齿微线段齿轮刚度，得到其刚度值较相应渐开线齿轮刚度值更优的结论，然而仿真计算的设置过程比较复杂。梁喜辉[2]等人采用势能分析法分析评价了行星齿轮组的啮合刚度。Howard[3]等人运用有限元模型对轮齿裂缝对于啮合刚度的影响进行了分析。Hedlund和Lehtovaara[4]采用有限元法对斜齿轮啮合刚度的变化进行了研究。Gu和Velex[5]提出了一种近似计算公式关于理想的直齿圆柱齿轮和斜齿轮啮合刚度。朱秋玲[6]等人采用有限元仿真法还有公式法研究了把啮合误差、时变啮合刚度考虑在内的齿轮非线性动力学系统。

本文采用的是累积积分势能法[7]，计算出双渐开线齿轮的综合啮合刚度以及单齿啮合刚度，通过这种方法研究齿轮啮合刚度受双渐开线齿轮哪些参数的影响。

1 累积势能法

在积累势能法中，啮合齿轮中储存的势能包括[8]：弯曲势能Ub，赫兹势能Uh，轴向压缩变形势能Ua、剪切势能Us，能够分别用于计算出弯曲刚度Kb、赫兹刚度 Kh、轴向压缩刚度Ka以及剪切刚度Ks，总啮合刚度为各刚度的串联形式[9]。根据弹性力学和材料力学理论可知，Ub、Uh、Ua以及Us表示如下：

其中，F是啮合点处的作用力；α1是F与横轴方向的夹角；Fa是径向力，F在X轴方向分力为Fa=Fsinα1；Fb是切向力，F在y轴方向分力为Fb=Fcosα1； G是切变模量；E是弹性模量；Ix是距离基圆x处轮齿截面的转动惯量；d为啮合点到基圆的距离；Ax为距离齿根圆x处轮齿截面面积；h为啮合点到轮齿对称线的距离。

根据公式(2)到(4)，得到弯曲刚度、剪切刚度以及轴向压缩刚度的计算公式：

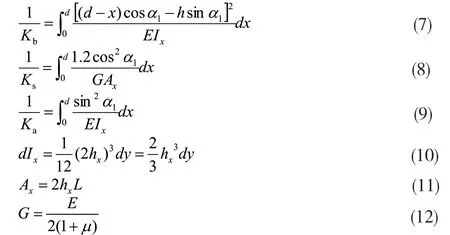
其中，hx是齿轮齿廓上的点到轮齿中线的距离；µ为泊松比。

根据渐开线齿轮齿廓的特点，hx的计算公式如下[10]：

其中，Rb是基圆半径。

通过公式可以得出，给定的齿轮，它的各个啮合点处的轴向压缩刚度Ka、剪切刚度Ks、弯曲刚度Kb只和啮合位置α1有关，与其他各参数是没有关系的。

对于相互啮合的两个齿轮，其总能量的表达式为：

其中，n是轮齿同时啮合的对数。

2 双渐开线齿轮不同参数对啮合刚度的影响

分阶式双渐开线齿轮(以下简称为双渐开线齿轮)综合了双圆弧齿轮以及渐开线齿轮这两种齿轮优点的一种新型齿轮[11]，这种齿轮是由两段相互交错的渐开线组成了工作齿廓，一段中间曲线连接了这两段渐开线，齿顶和齿根这两段渐开线齿廓是呈阶梯式布置，如图1所示。在双渐开线齿轮啮合的过程中，啮合刚度的呈现周期性变化，这也是为什么会产生噪声以及激励齿轮振动的主要原因之一，双渐开线齿轮动力学特性研究的基础是研究啮合刚度计算方法。

图1 双渐开线齿轮端面齿廓

齿轮啮合刚度反映的是齿轮轮齿从刚进入啮合到退出啮合这整个过程中的动态参数，齿轮参数不同。比如，改变齿轮的齿宽、模数等参数,啮合刚度也会随之改变，因此，需要研究双渐开线齿轮模数以及齿宽对齿轮啮合刚度的影响规律。

2.1 有限元模型的建立

建立双渐开线齿轮三维有限元模型，见图1。在轴向和径向这两个方向上施加固定约束，双渐开线齿轮轮廓上施加一个沿接触线的线性分布力F，可以得到沿力F方向的平均挠度δ。

轮齿的单齿啮合刚度为：

对于啮合的齿轮来说，力的作用是相互的，主从动轮相接触的地方都收到一个有相同的力F。一对齿轮会有两个挠度δ1和δ2，因此单齿啮合刚度可以用如下公式表示：

一对轮齿在任意接触位置的综合啮合刚度K12是这两个单齿啮合刚度K1和K2的并联形式。因此，K12可以表示为：

当多齿同时啮合时，在任意指定的接触位置的综合啮合刚度Ktotal可以表示为：

n是同时啮合的齿轮齿对数。

2.2 模数的影响

首先设定齿轮参数，齿宽L=25mm，螺旋角 ，其他参数保持不变。模数设为mn=3mm-4.5mm，模数不同的渐开线齿轮的综合啮合刚度和单齿啮合刚度如图2所示。

从图中可以看出：综合啮合刚度与单齿啮合刚度的走势明显不同，图2(a)中单齿啮合刚度随着转角的不同，变化趋势较小，这单齿啮合刚度的啮合稳定性好。而图2(b)和(c)中对于的双渐开线齿轮的单齿啮合刚度随着转角的变化变化趋势较大。

根据公式(16)可以得出，齿轮模数越大，端面基圆节距就会增大，主动轮齿宽值随之增大，然而从动轮齿宽值则不变。因此轮齿啮合接触面宽度就会增加。模数增加的话，双渐开线齿轮综合啮合刚度波动随之增加。如图(a)所示，当齿轮模数为mn=3mm时，双渐开线齿轮的综合啮合刚度趋于一条直线。而齿轮模数mn=4.5mm时，最大值与最小值的差为。

图2 不同模数下的啮合刚度

2.3齿宽的影响

设定双渐开线齿轮的模数mn=4mm，螺旋角β15。，其他参数保持不变，齿宽设定为10—25mm这个范围区间，综合与单齿的啮合刚度如图3所示。由图可知，齿面宽度增加的时候，双渐开线齿轮的单齿啮合刚度曲线先变化较为剧烈，随后趋于平缓，根据公式(13)和(14)可以分析得出，主动轮齿宽值减小，从动轮齿宽值增大。单齿啮合刚度的斜率会随着齿宽的增大而呈减小的趋势。同理可得，齿宽增大，综合啮合刚度曲线也是趋于平缓。

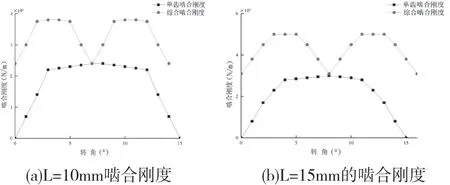
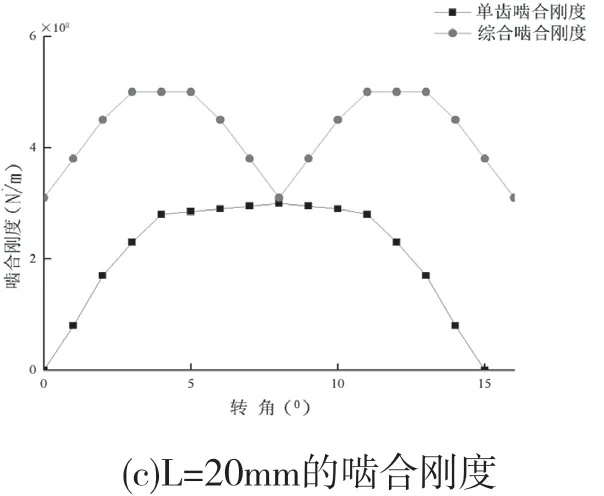
图3 不同齿宽下的啮合刚度

3 结论

本文在累积积分势能法基础上建立了双渐开线齿轮啮合刚度的计算模型，并对比了双渐开线齿轮齿宽、模数这两种因素对啮合刚度的影响。随后计算分析了双渐开线齿轮一对轮齿的综合啮合刚度以及单齿啮合刚度。根据累积积分势能法计算双渐开线齿轮的啮合刚度时。从模型计算中可以清楚的看出双渐开线齿轮的啮合刚度变化的规律。从中可以看出，模数的增加，会使啮合刚度的变化趋势较为剧烈，双渐开线齿轮的啮合刚度曲线随着齿宽的增加而减小。