基于Laguerre滤波器的核范数子空间辨识

于 淼 刘建昌 王洪海 张文乐

(1.东北大学秦皇岛分校控制工程学院，河北秦皇岛 066004;2.东北大学信息科学与工程学院，辽宁沈阳 110819;3.东北大学流程工业综合自动化国家重点实验室，辽宁沈阳 110819;4.华东理工大学信息科学与工程学院，上海 200237)

1 引言

近年来，子空间辨识作为系统辨识的重要分支已引起控制领域专家学者的浓厚兴趣[1-5].其中大多数方法都是解决离散时间系统的辨识问题，并依据所得模型进行数字控制器的设计.然而，与离散时间系统的辨识相比较，连续时间系统的辨识在参数估计，H∞控制和自校正控制等方面应用更加广泛[6-7].此外，多数物理现象都具有连续属性，描述它们的数学模型是微分方程.因此，针对连续时间系统辨识问题提出相应的解决方案具有重要的理论意义和实际价值.

辨识连续时间系统的主要方法可归类为直接法和间接法.间接法是依据输入输出数据估计离散时间系统，然后将其转化为连续时间系统.然而，这种系统转换过程可能存在采样时间难以选择，矩阵对数的运算复杂，离散时间系统的零点到连续时间系统的极点难以转换等问题[8-9].直接法是直接依据输入输出数据估计连续时间系统.然而，直接法辨识系统的一个难点问题是如何正确处理输入输出变量的时间导数.目前有很多方法克服了重构时间导数的困难.文献[9]通过Laguerre滤波器处理输入输出信号，研究了基于Laguerre滤波器的子空间辨识方法.文献[7]采用泊松矩函数(Poisson moment functionals，PMF)方法解决了输入输出时间导数和积分的估计问题，并与子空间辨识方法相结合辨识了连续时间模型.在文献[10]中，作者利用随机分布理论得到了分布意义下的输入输出信号的时间导数，从而推导出相应的输入输出代数方程，并利用提出的新方法得到了连续时间随机系统.在文献[11]中，作者通过Laguerre滤波和Laguerre投影处理输入输出信号，提出了基于Laguerre滤波的子空间辨识(subspace identification via Laguerre filters，LFSID)方法.

虽然上述子空间辨识方法解决了连续时间系统的时间导数求解问题，但是都使用了奇异值分解去估计系统阶数，这种处理方式带来了新的问题，即当存在过程噪声和测量噪声时，如何获取最优的系统阶数[12].这种构建低秩矩阵逼近的秩最小化问题是一个非确定性多项式困难(non-deterministic polynomial-hard，NP-hard)问题[13]，核范数最小化方法是解决此问题的有力工具.由于具有逼近矩阵的秩最小化和相应的线性性质，核范数最小化方法已经成功地应用于系统辨识的研究之中[14].文献[15]通过半正定规划描述核范数最小化问题，利用内点法求解此优化问题，并且将提出的方法应用于线性系统的辨识中.在文献[16]中，作者研究了基于加权核范数最小化的子空间辨识方法，并采用交替方向乘子法求解此优化问题.文献[17]基于文献[18]研究了核范数系统辨识方法，并且将其应用于缺失输入输出数据的随机系统中.在文献[12]中，作者提出了频域的核范数最小化子空间辨识方法，并且研究了模型阶数和残差的Pareto最优轨迹问题.文献[3]探索了基于Pareto优化的核范数子空间辨识方法，并建立了新息形式的多变量状态空间模型.

可见，核范数最小化方法能够有效处理NP-hard问题，从而获得低秩矩阵逼近.目前核范数最小化方法对于带有过程噪声和测量噪声的连续时间随机系统的辨识涉及较少.在实际的生产过程中，过程噪声和测量噪声的存在给连续时间系统的辨识带来了一定的困难，如难以确定系统的阶数等.因此，当系统阶数未知时，应用核范数最小化方法去解决带有过程噪声和测量噪声的连续时间随机系统的辨识问题是一个挑战.

本文对基于Laguerre滤波器的核范数子空间辨识方法进行深入研究，有效地解决了带有过程噪声和测量噪声的连续时间随机系统的辨识问题.本文其他部分构成如下:2)问题描述;3)采用Laguerre滤波器获得系统的输入输出代数方程;4)通过核范数子空间辨识方法确定系统的最优阶数，并且分别得到模型的系统矩阵和噪声强度;5)通过数值仿真验证所提方法的有效性和精确性;6)给出结论.

2 问题描述

考虑如下连续时间随机系统[18]:

其中:X(t)∈Rn是状态向量;Y(t)∈Rl是输出向量;A ∈Rn×m，C ∈Rl×n是系统矩阵;W(t)∈Rn，V(t)∈Rl是高斯白噪声，其协方差矩阵为

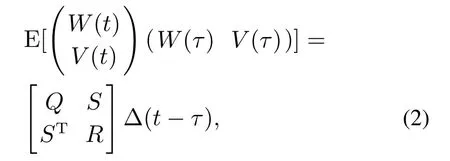
其中:E(·)是期望算子，Δ(t-τ)是Dirac delta函数.本文的目的是根据输入输出数据确定系统阶数和系统矩阵A，C.

根据式(1)，得到代数关系如下:

矩阵Γi∈Rli×n(i ＞n)是广义能观性矩阵，矩阵Hi∈Rli×mi是低阶分块三角矩阵.它们定义为[19]

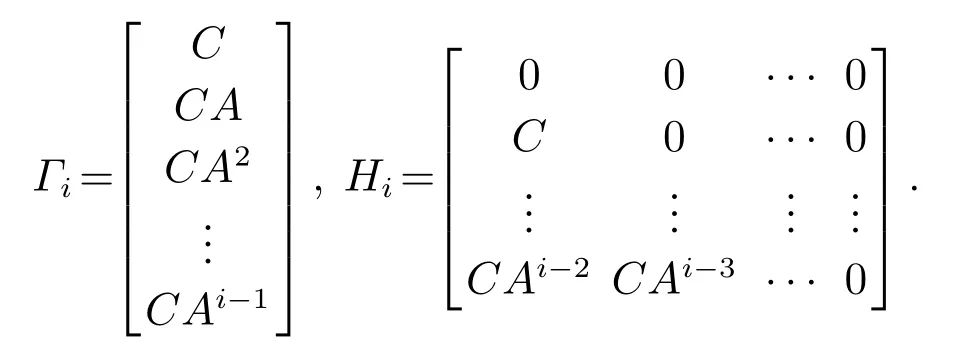
一方面，系统矩阵A，C可以通过矩阵Γi和矩阵Hi导出.对于式(4)，Yi存在至少(i-1)阶导数是必要条件.然而对于随机情况，噪声W(t)和V(t)是高斯白噪声过程，处处不可微.并且状态X(t)和输出Y(t)也不存在时间导数.另一方面，通过对输入输出投影矩阵的奇异值分解可以得到矩阵Γi的列空间.理论上，奇异值的个数等于系统的阶数[20].然而，由于噪声的影响，在构造低秩矩阵逼近的过程中如何获取最优的系统阶数是一个难点问题.

针对上述带有过程和测量噪声的连续时间随机系统的辨识问题，本文提出了基于Laguerre滤波器的核范数子空间辨识(nuclear norm subspace identification based on Laguerre filters，NLFSID)方法.具体地，推导了系统的输入输出代数方程，详见第3节;解决了获得系统最优阶数的问题，详见第4节.

3 输入输出代数方程的建立

本小节通过Laguerre滤波器解决输入输出时间导数难以求解的问题.为了获得输入输出代数方程，给出以下定义.

定义L2(R+)表示平方可积空间和时间区间0 ＜t＜∞的Lebesgue可测函数，内积定义为

空间H2是L2(R+)的闭子空间[9].一阶全通滤波器为

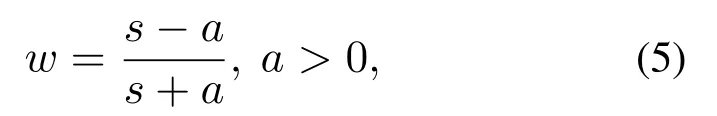
其中符号w表示算子.

定义li(t)是i阶全通滤波器的时域表示.[liy](t)是y(t)和li(t)的卷积，表示为

一组Laguerre滤波器可以通过全通滤波器得到.零阶Laguerre滤波器为

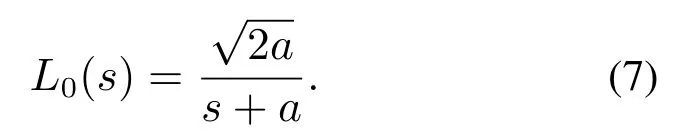
式(7)乘式(5)，得到一阶Laguerre滤波器

以此类推，第i阶Laguerre滤波器为

至此获得一组Laguerre滤波器，它的结构如图1所示.

并且L0(s)至L4(s)Laguerre滤波器的脉冲响应函数如图2所示.

根据式(5)和式(9)，有以下关系:

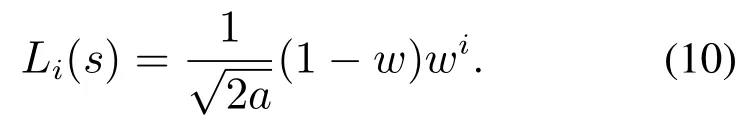
根据式(5)，系统(1)可以转换为以下形式状态空间模型:

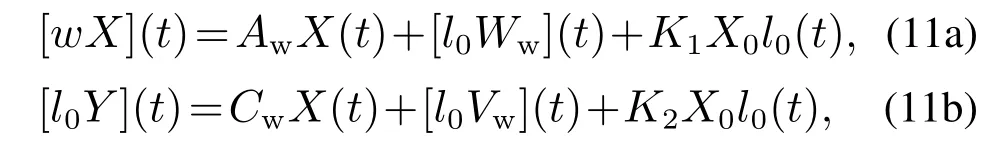
其中:初始状态X0=0，

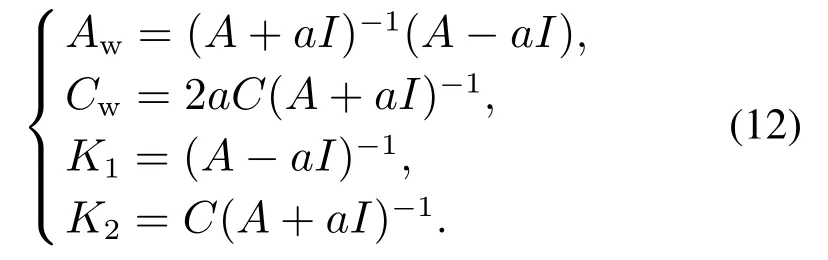
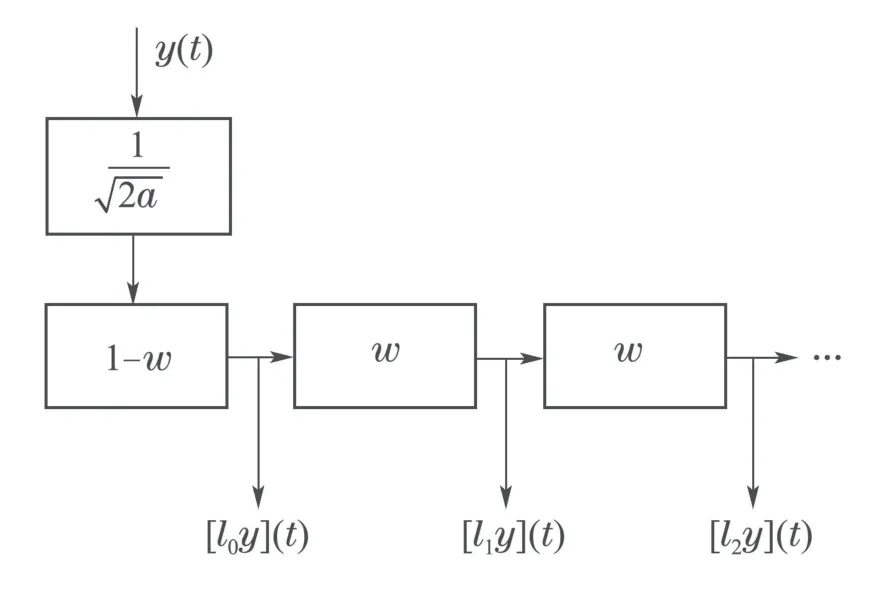
图1 一组Laguerre滤波器的框图Fig.1 Block diagram of a Laguerre filter bank

图2 L0(s)至L4(s)Laguerre滤波器的脉冲响应函数Fig.2 Impulse reponse functions of the Laguerre filters L0(s)up to L4(s)

新的噪声过程Ww和Vw表示为

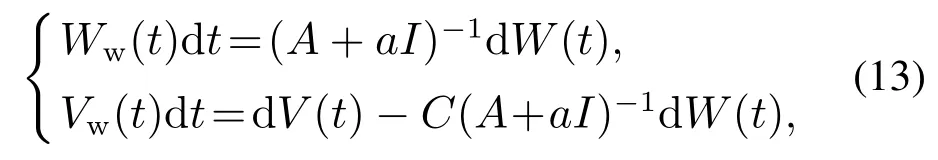
其协方差矩阵为

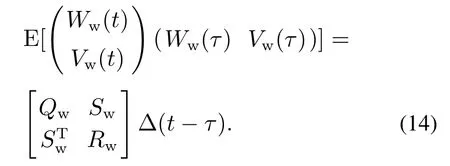
根据式(10)-(11)，得到输入输出代数方程

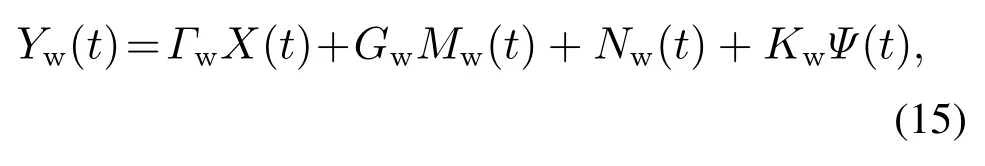
其中:

4 核范数子空间辨识

通过时刻{tk，k=1，2，···，N}(-∞＜tk＜∞)的输出数据，得到矩阵Yw:

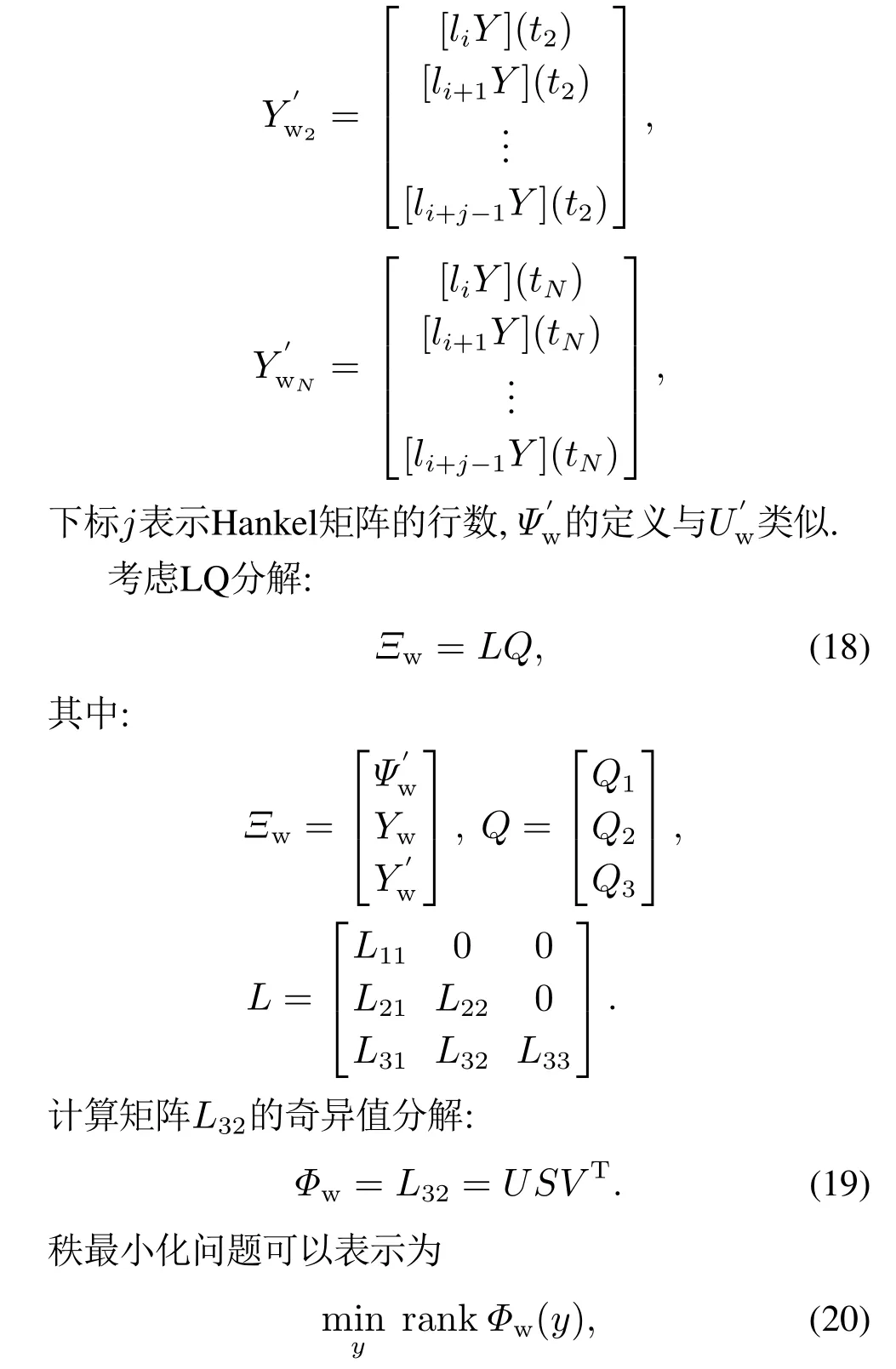
其中y是最优变量.

式(20)是一个NP-hard问题[21]，而核范数最小化方法可以解决该问题，基于此上式转化为

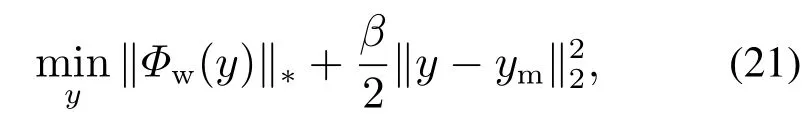
其中:‖·‖*是核范数，Φw(y)是线性函数，β是加权参数，ym是通过Laguerre滤波器得到的测量输出序列.

优化问题(21)可以通过交替方向乘子法求解.定义新变量Zw=-Φw(y)，则问题(21)的增广拉格朗日函数为

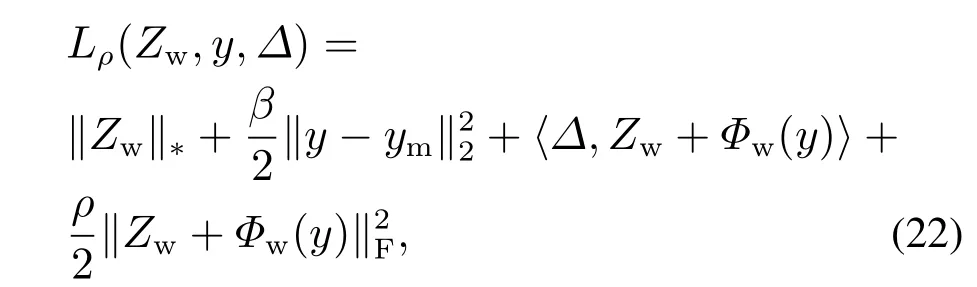
由Zw-最小化，y-最小化和Δ-更新构成交替方向乘子法.

根据式(22)，有

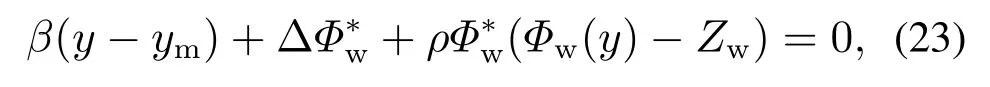
根据文献[22]的迭代算法及式(23)，可得

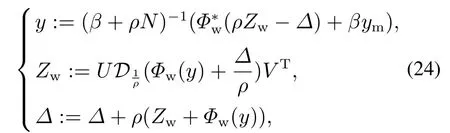
其中:U，V 可以通过奇异值分解得到;

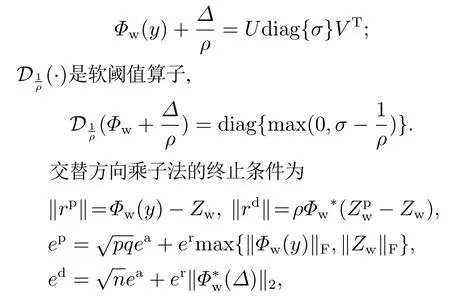
其中:rp是原始残差，rd是对偶残差，ep是原始承受量，ed是对偶承受量，ea是绝对误差，er是相对误差，n是测量输出数据长度，矩阵是Zw之前迭代数值.

采用以下更新方程代替采用固定惩罚参数ρ，改进交替方向乘子法的收敛速度:

其中µ＞1和τ ＞1是参数(一般µ=10，τ=2).

从方程(24)的最优解Φw(y)，计算奇异值分解:

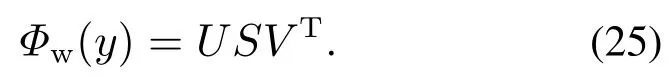
进一步，

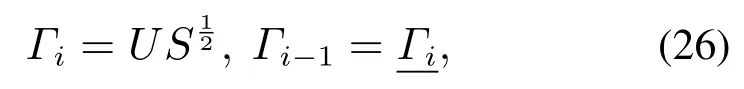
根据式(25)及文献[6]，卡尔曼状态序列为

系统矩阵可以通过以下方程求解:

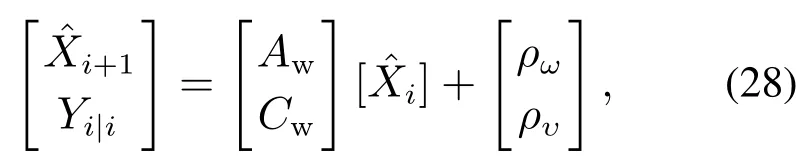
其中ρω和ρυ是Kalman滤波残差.

噪声强度为

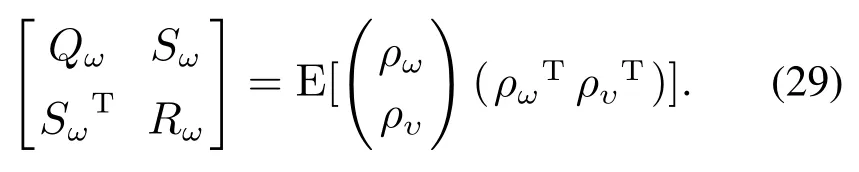
根据式(28)的系统矩阵和式(12)，得到系统矩阵A，C，由式(25)估计系统(1)阶数.至此完成了连续时间随机系统的辨识过程.

本文基于Laguerre滤波器的核范数子空间辨识(NLFSID)方法可归纳如下:

步骤1依据式(9)，得到通过Laguerre滤波器的输入信号;

步骤2通过式(10)-(11)，得到系统的输入输出代数方程;

步骤3根据式(20)，构造秩最小化问题;

步骤4由式(22)-(24)，采用交替方向乘子法对优化问题进行求解;

步骤5由式(25)-(29)，获得系统阶数以及连续时间随机系统的模型.

5 仿真研究

本节通过数值例子的仿真实验验证了提出NLFSID方法的有效性、精确性及比较优势.考虑如下两输入两输出连续时间随机系统[8]:

e(t)为零均值单位方差的高斯白噪声过程，输出信号为根据系统(30)得到的仿真输出，N=1000，输入输出信号连续采样时间为Ts=0.01 s，执行100次蒙特卡罗仿真.

分别采用NLFSID 与LFSID 方法对系统(30)进行辨识，得到的规范化奇异值指标的平均值如图3所示，图中给出了分别由两种方法辨识得到的式(19)中矩阵Φw的规范化奇异值平均值.

根据最大奇异值的个数确定系统阶数.可以看出，LFSID的奇异值很接近，这使得模型的阶数确定非常困难.相比之下，NLFSID的奇异值具有显著性差异，从而确定模型阶数更容易.

分别采用NLFSID与LFSID方法对系统(30)进行辨识，得到相应的方法辨识模型的平均伯德图如图4-5所示.

可见无论频率高低，NLFSID比LFSID得到的模型更接近真实模型的伯德图曲线(30)、系统辨识的精度更高.

图3 NLFSID与LFSID的最大奇异值指标平均值Fig.3 The averaged index of largest singular values index of the NLFSID and LFSID

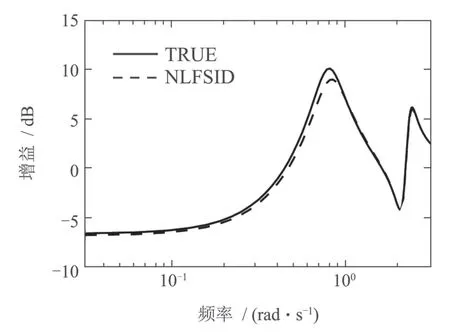
图4 NLFSID模型的平均伯德图Fig.4 Averaged bode plot of NLFSID model

采用两种方法获得系统(30)的模型后，得到相应的NLFSID与LFSID的零极点平均值如图6-7所示.从图形中可见NLFSID比LFSID得到的结果更接近真实模型的零极点、辨识模型更精确.

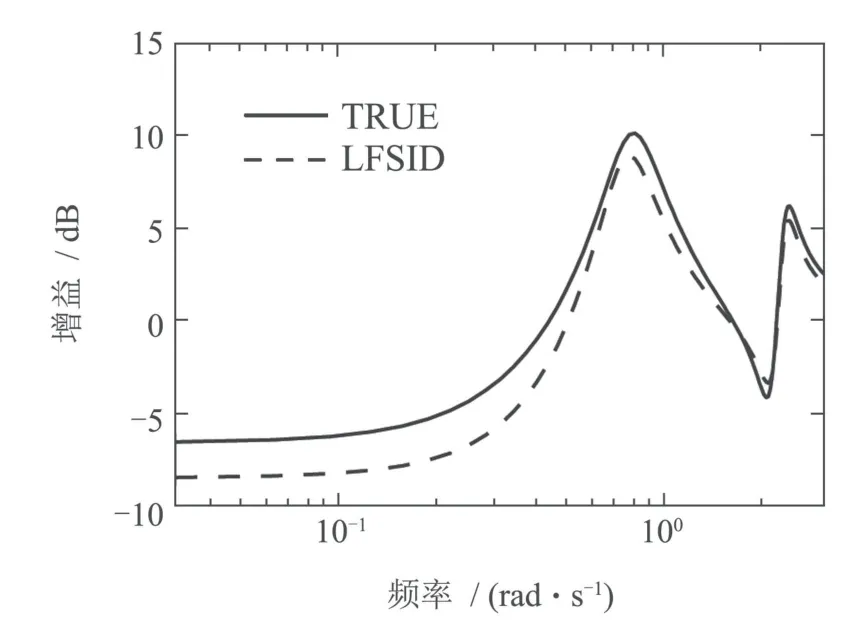
图5 LFSID模型的平均伯德图Fig.5 Averaged bode plot of LFSID model

图6 NLFSID模型的零极点平均值Fig.6 Pole-zero average of NLFSID model

图7 LFSID模型的零极点平均值Fig.7 Pole-zero average of LFSID model

6 结论

本文提出了一种基于Laguerre滤波器的连续时间随机系统的核范数子空间辨识方法.利用Laguerre滤波器对数据进行处理，避免了输入输出Hankel矩阵的时间导数计算.通过核范数最小化方法获得最优的系统阶数，并采用交替方向乘子法解决此优化问题.最后，通过数值例子的比较仿真实验验证了提出方法的有效性和精确性，并说明了本方法更容易获得模型阶数、辨识精度更高的优势.