滑模观测器在大惯量扫描镜系统中抗谐振的应用

李家骏 ，王淦泉

(1.中国科学院红外探测与成像技术重点实验室，上海 200083;2.中国科学院上海技术物理研究所，上海 200083)

1 引言

随着空间载荷技术的发展，对于卫星成像技术的要求与日俱增，而扫描镜控制系统的控制精度直接影响到成像质量.而因电机与扫描镜之间柔性连接而引起的机械谐振是制约控制系统精度的一个重要原因，对于本文所研究的扫描镜控制系统，具有扫描镜转动惯量较大的特点，谐振频率大概在90～200 Hz之间[1].机械谐振会导致控制性能下降，带宽难以提高，机械装置磨损增大.

谐振抑制方法主要分为被动抑制以及主动抑制.被动抑制在不改变系统结构的前提下，通过在控制回路中串入陷波器来抑制谐振[2-3]，由于该方法无需改变控制器结构，且实现简单，因此在工业上被广泛运用.但该方法离线时需准确测得谐振频率且系统运行时谐振频率不能发生改变，在线辨识谐振频率时运算量过大，并且不能解决系统中存在多个谐振频率的情况.

主动抑制通过改变控制器结构来抑制系统的机械谐振，主要包括以下几种方法:

1) 基于电机侧的信息，借助观测器，观测出电机或负载侧的信息进行补偿，从而抑制谐振[4-5].该方法在抑制谐振影响的同时，可以确保伺服系统控制回路的稳定性[6].反馈的信息中包括电机加速度反馈[7]、负载转矩反馈和负载速度反馈等.观测器则包括隆伯格观测器[1]、滑模观测器[8]和自适应观测器[9]等.该方法适用范围广，谐振抑制效果明显，但是控制效果受限于观测器带宽及精度.

2) 不采用附加的观测器，仅改进控制器结构，如基于极点配置的PID控制[10-11]，新型控制方法如自抗扰控制[12]、滑模控制、重复控制[13]等，此类方法控制精度高，但多存在结构复杂、非线性性强、实现困难等问题，对硬件的要求也较高.

针对谐振抑制问题，文献[1]利用线性观测器观测出电机加速度进行反馈，证明了加入电机加速度反馈等于变相增大了电机的转动惯量，成功抑制的机械谐振.文献[14]采用负载速度反馈，证明了该方法能明显提高二质量系统的稳定性及控制性能.文献[8]采用滑模观测器来观测电机加速度进行反馈，但是仅仅利用了滑模观测器观测出的加速度信息，而同样观测出来的负载侧信息并未加以利用.同时，该控制器并未进行数字化，仅仅在连续系统下进行了仿真，不具有应用价值，需要抑制的谐振频率也较低，并不适用于卫星平台中大惯量负载和角秒级控制精度的扫描镜控制系统的分析.

本文在文献[8]滑模观测器的基础上加以改进.针对大负载惯量，高精度要求的扫描镜伺服系统，利用滑模观测器可以观测出系统多个状态的优点，将电机加速度反馈和负载速度反馈相结合，建立连续与离散混合模型进行仿真验证，在达到抑制谐振的同时保持较高的控制精度(＜1′′).同时还分析了传感器噪声对控制性能的影响，该控制方法的鲁棒性以及与同类方法的对比.

2 系统建模

2.1 二质量伺服系统建模

由于扫描镜与电机之间的传动机构并非理想刚体，电机运行时负载不能被视为与电机为一个整体，因此建模时应将负载分离为一个独立的整体，即二质量系统[15].二质量伺服系统的力学模型如图1所示.

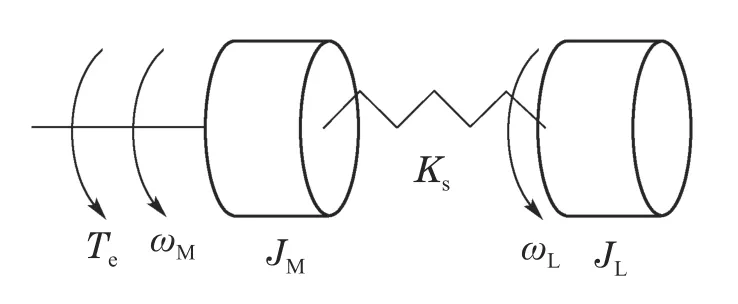
图1 二质量系统力学模型Fig.1 Two-mass system mechanics model

二质量系统模型已被广泛研究[1，7，9，15]，现根据文献[15]及图1建立系统的动力学方程:

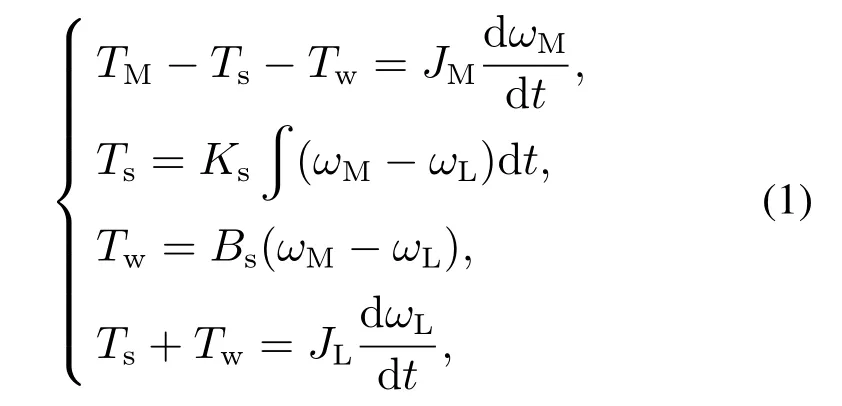
式(1)中:TM为电机电磁转矩，JM为电机转动惯量，JL为负载转动惯量，ωM为电机速度，ωL为负载速度，Ts为弹性阻尼矩，Tw为黏性阻尼矩，Ks为弹性轴刚度系数，Bs为黏性阻尼系数.

根据式(1)可以建立二质量伺服系统柔性连接结构框图如图2所示.

图2 二质量系统结构框图Fig.2 Two-mass system block diagram

结合式(1)，图2及自动控制原理的相关知识，可以推导出电机速度ωM和电磁转矩TM之间的传递函数

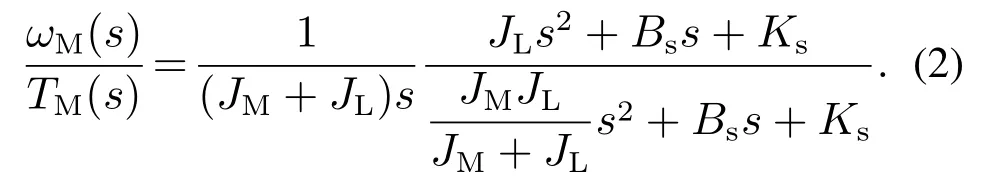
根据式(2)可以得到谐振频率ωFR以及反谐振频率ωAR的表达式，其中黏性阻尼系数Bs由于较小可以忽略.

2.2 谐振对控制系统性能的影响

可以看出，由于机械谐振的存在，电机端速度会出现振荡.这是由于当谐振频率与系统相位穿越频率接近时，系统开环增益将被拉高，使系统处于临界稳定状态甚至不稳定.机械谐振降低了系统的稳定裕度，限制了速度环带宽的提高.

图3 谐振系统与刚性系统的速度阶跃响应Fig.3 Speed step response of resonant and rigid systems

2.3 速度环引入电机加速度及负载速度反馈

根据文献[1]可知，在速度环加入电机加速度反馈相当于将电机的转动惯量从JM增大到(1+KFAB)JM，其中KFAB为电机加速度反馈系数，此时的谐振频率及反谐振频率如下式所示:

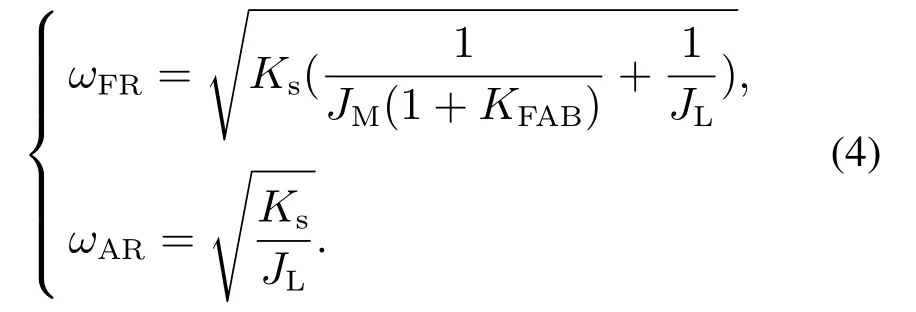
对比式(3)可以看到，谐振频率明显降低，表明加入电机加速度反馈有效地抑制了机械谐振.

同时，在大部分电机控制中，反馈装置都装在电机上，当电机与负载之间采用柔性连接时，电机位置与负载位置之间的关系会发生改变.反馈到系统中的电机位置及速度并不能精确反应负载状态，会影响控制系统的精度.因此加入负载速度反馈后，可以有效提高控制系统精度，同时，由于对实际负载位置形成闭环，还使得控制系统对电机与负载柔性连接中的延时不敏感[6].

3 滑模观测器设计

本文采用电机加速度及负载速度双反馈，反馈信息由文献[8]中的观测器获得，该观测器为一种基于扰动的滑模观测器，在掌握系统结构信息的基础上，利用实际系统的输入iq及输出θM作为该观测器的两个输入或扰动，以电机与负载的位置，速度及加速度为系统状态构建滑模面，通过设置恰当的切换控制律，使系统状态按照滑模运动趋近于平衡点，从而达到了观测与跟踪的效果.

对于本文的被控对象，系统结构由永磁同步电机负载谐振在d，q坐标系下带加速度变量的高阶系统方程表示[8]:

将式(5)写成矩阵形式

式中:x=[θMθLωMωLaMaL]T为系统状态，

将实际系统的输入即q轴电流iq视为观测器的未知扰动，实际系统的输出量即电机位置θM视为观测器的输入，构建滑模面s=切换控制律选择等速切换控制律u=-K sgn s，则基于扰动的滑模观测器形式如下[16-17]:

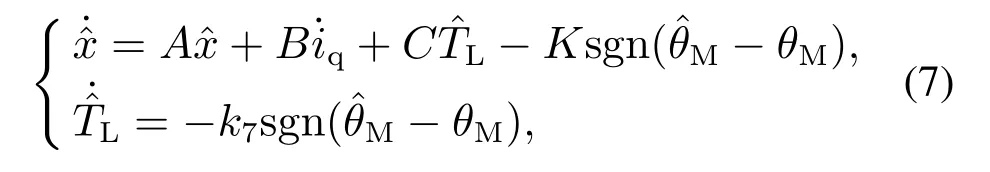
滑模观测器的任务就是在扰动iq的作用下，根据滑模面设计恰当的切换控制律参数K，使得系统各状态x=[θMθLωMωLaMaL]T沿滑模面运动趋近于观测值，从而达到观测的目的，即使式(7)精确跟踪式(6).

因此，观测器的设计分为两部分:一是根据被控对象参数建立接近于实际系统的系统矩阵A，B，C;二是针对本文的被控对象设计合适的切换控制律参数K.滑模观测器是一种非线性观测器，因此无法使用传统的传递函数法计算出控制参数，但由于本文的滑模观测器中采用的是等速切换控制律[8]，而等速切换函数中K代表了系统状态趋近于滑模面的速度及到达滑模面后的运动状态，因此可以通过滑模控制的一般经验设计控制参数K.

4 仿真验证

4.1 仿真参数设置

仿真参数设置如下:电机转动惯量

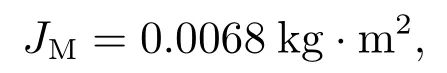
负载转动惯量JL=0.0612 kg·m2，力矩系数Kt=0.157 Nm/A，刚度系数Ks=5436 Nm/rad，定子电阻R=1.4 Ω，定子电感L=1.7 mH，极对数p=6，磁通量ψf=0.0175 Wb，滑模观测器切换函数控制参数k1=k2=1，k3=k4=k5=k6=10，k7=1;此时谐振频率计算为150 Hz.位置环采样频率为200 Hz，速度环采样频率为800 Hz，电流环及滑模观测器采样频率为16 kHz.以下仿真除特殊说明均为该参数.

根据上文对滑模观测器的设计，此时的滑模观测器为

2.3.1 推荐对于消化道出血风险高危的患者DAPT治疗联用PPI(Ⅰ,B)[9]：虽然使用PPI不增加心血管事件风险的证据是有奥美拉唑研究获得，基于药物与药物相互作用研究，奥美拉唑和艾美拉唑似乎具有最高倾向的临床药物相互作用，而泮托拉唑和雷贝拉唑的药物相互作用倾向最低。

4.2 双反馈对系统性能的提升

本节中给出阶跃响应和摆动响应两组系统的时域响应，以验证滑模观测器对系统性能的提升.

仿真结构如图4所示，其中电机与扫描镜之间的谐振结构根据图2搭建.

图4 扫描镜控制系统结构框图Fig.4 Two-mass system block diagram

1) 阶跃响应.

当速度指令为1 rad/s的阶跃信号时，仿真结果如图5所示.

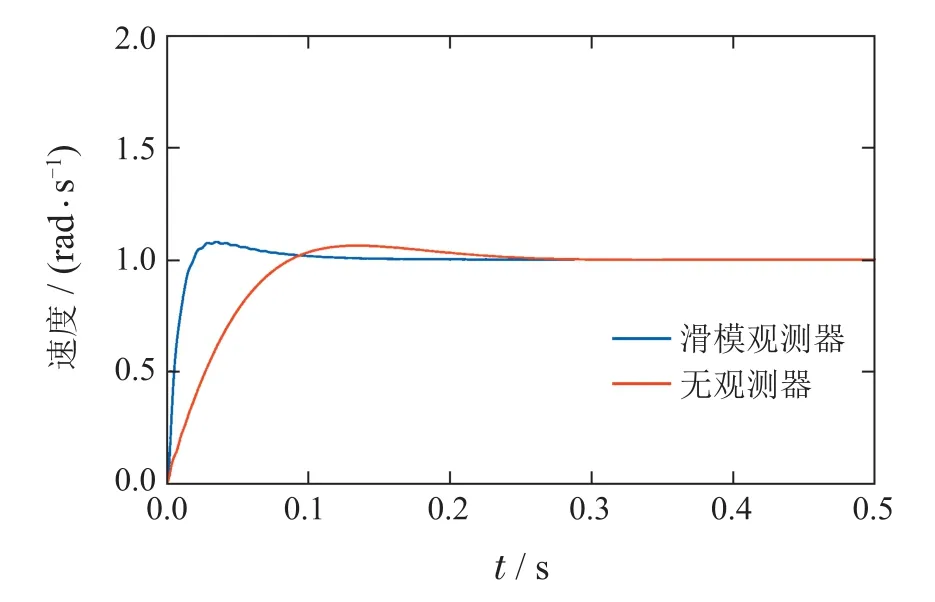
图5 负载速度阶跃响应Fig.5 Load speed step response

可以看出，在保持超调量一致的前提下，加入滑模观测器后系统明显具有更快的上升时间和更短的调节时间.

表1中，上升时间为系统第1次到达终值的时间，调节时间为系统稳定在2%误差带内的最短时间.

表1 时域性能指标Table 1 Time domain performance indicator

摆动信号为电机经加速、匀速、减速3个阶段共转动0.3 rad后，停留0.4 s反向运行的周期信号，如图6所示.负载位置误差曲线如图7所示.

可以看出，加入滑模观测器后，系统的位置响应在匀速段明显具有更高的精度以及更快的调节时间.此时的匀速段位置误差均方根如表2所示.

图6 位置指令Fig.6 Position command

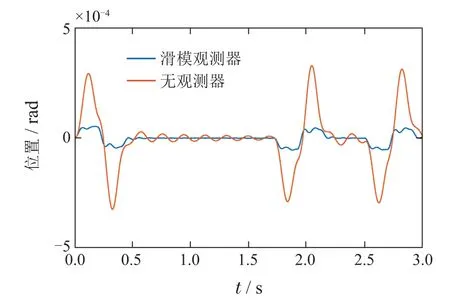
图7 负载位置误差Fig.7 Load position error

表2 负载位置均方根误差值Table 2 RMS value of load position

4.3 传感器噪声对控制性能的影响

本节将分析在存在位置传感器噪声的情况下，滑模观测器的控制性能.输入信号为上节中的摆动信号.

1) 位置传感器的分辨率噪声.

位置传感器以有限的分辨率给出未知的量化离散值，控制器对每个采样间隔采用简单的差分运算估计速度，这样会在位置传感器的每一步都产生一个采样时间宽度的脉冲，由此产生电流尖峰，这也是许多伺服系统中造成噪声的一个重要原因.图8为不同分辨率噪声下，位置跟踪误差响应.表3给出位置均方根误差值.

可以看到，即使位置传感器的位数只有16位，与24位时相比，精度也仅相差了一个数量级.因此可以说滑模观测器对位置传感器分辨率噪声具有较好的抑制能力.

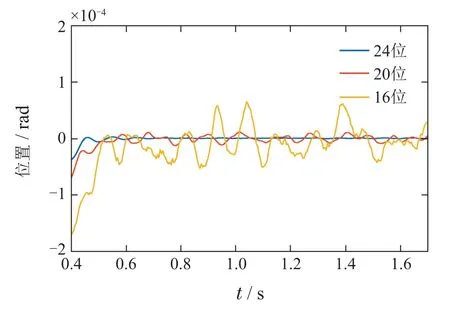
图8 不同分辨率下的负载位置误差Fig.8 Load position error under different resolutin noise

表3 负载位置均方根误差值Table 3 RMS value of load position

2) 位置传感器的测量噪声.

在实物实验时，位置传感器的最后几位数据有时并不准确，当24位位置传感器的最后4位存在测量误差时，位置传感器的测量误差将达到1角秒以上.图9为加入不同幅值的随机噪声时的位置跟踪误差响应，表4给出位置误差均方根值.

图9 不同测量误差噪声下的负载位置误差Fig.9 Load position error under different measurement error noise

表4 负载位置均方根误差值Table 4 RMS value of load position

可以看到，滑模观测器对测量噪声具有一定的抑制作用，但是系统的精度仍然受到传感器测量精度的制约.

通过上述对噪声的分析，可知加入滑模观测器后系统对位置传感器噪声具有较好的抑制能力.但是想要进一步提高控制精度及控制性能，就需要更高分辨率及更高精度的位置传感器.本文的位置传感器采用文献[18]的设计:分辨率为24位的感应同步器，测角精度小于1′′，转换频率为327 kHz，带宽约为300 Hz.因此保证了位置反馈拥有较高的分辨率及精度，尽量减小了位置传感器对控制性能的制约.

4.4 观测器计算频率对控制性能的影响

本节将分析滑模观测器的计算频率对控制系统性能的影响，表5为计算频率分别为8 kHz，10 kHz，16 kHz，32 kHz时的位置均方根误差值.

表5 负载位置均方根误差值Table 5 RMS value of load position

可以看到，更快的观测器计算频率可以带来更高的控制精度，根据文献[19]的研究，在电流环采用16 kHz，速度环采用800 Hz，位置环采用200 Hz的采样频率下，控制芯片仍有足够的计算资源完成复杂的观测器运算，即使观测器运算空间不足时，适当减小计算频率只会损失很少的控制精度.

4.5 建模不准确对控制性能的影响

不同于基于传递函数的线性观测器设计，滑模观测器的建模与设计依赖于被控对象的参数[8]，因此对被控对象的参数是否敏感将成为该控制方法是否具有实用价值的一个评判标准.本节将分析在建模参数不准确，而控制器参数不发生变化时，该控制方法的控制性能.输入信号为摆动信号.

1) 刚度系数建模不准确.

仿真中刚度系数为5436 Nm/rad，当实际系统中刚度系数略小于建模的刚度系数时，被控对象发生改变，谐振频率降低，开环增益太大时，可能导致系统失稳.在不改变控制器参数的情况下，假设刚度系数建模为误差20%，此时的位置均方根误差值如表6所示.

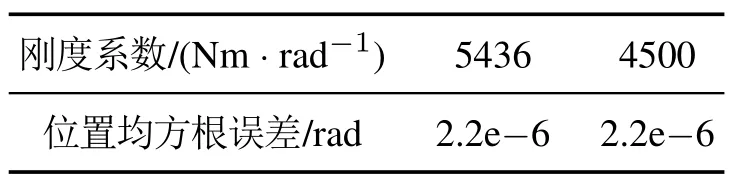
表6 负载位置均方根误差值Table 6 RMS value of load position

2) 转矩常数.

转矩常数一般由电机手册中给出，但是转矩常数很容易受到各种因素的影响，会导致电机转矩与电流的关系发生改变，从而降低系统的控制精度[20].假设转矩常熟建模误差30%，此时的位置均方根误差值如表7所示.

表7 负载位置均方根误差值Table 7 RMS value of load position

3) 粘滞摩擦系数.

粘滞摩擦系数的测量比较复杂，容易产生建模不准确[21].分别取粘滞摩擦系数为0.01 Nm·s/rad，0.0001 Nm·s/rad，0.001 Nm·s/rad，此时位置均方根误差值如表8所示.

表8 负载位置均方根误差值Table 8 RMS value of load position

由以上分析可知，当刚度系数、转矩常数和粘滞摩擦系数3个主要参数存在建模不准确时，滑模观测器控制方法存在较好的鲁棒性.

4.6 相同被控对象下与同类方法的比较

文献[1]中采用一种线性观测器观测出加速度并将其反馈至速度环，仿真结果表明，对于大惯量，高精度的被控条件，该方法有效抑制了机械谐振.现将文献[1]中的方法与本文的方法进行比较，仿真结果见表9.

表9 基于两种观测器的谐振抑制对比Table 9 Comparison of resonance suppression based on two observers

可以看到，在电机位置均方根误差相差不多的情况下，由于本文提出的方法同时采用了负载速度反馈，因此对于负载位置的提升效果更为明显.

5 结论

针对带有大负载的扫描镜谐振系统，本文设计了滑模观测器，采用电机加速度和负载速度的双反馈对此类谐振进行了抑制.仿真结果表明:与未采用观测器时相比，本文的方法有效地抑制了机械谐振，系统拥有更快的响应速度，更高的稳态精度，达到了设计要求(＜1′′).同时设计的滑模观测器对位置传感器的噪声具有较好的抑制效果，且具有较高的鲁棒性和较广的适用范围.