一类时变系统的多模型切换动态调节控制算法

王 岩，王 昕 ，王振雷

(1.华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237;2.上海交通大学电工与电子技术中心，上海 200240)

1 引言

在实际工业过程中，被控对象经常是一个复杂系统，其工作点可能会随着环境变化、设备老化等因素发生变化，导致被控对象的结构参数等也因此发生改变.在这种情况下，系统的不确定区域会随之扩大.此时，不仅是基于单一模型的自适应控制[1]或增益调度[2]会有较差的暂态性能，而且对于多模型自适应控制，若不大量增加模型数量，其控制效果也会难以满足指标要求[3].因此，如何在控制模型数量增长的同时，更好地改善被控系统的性能显得尤为重要.

切换线性变参数(linear parameter varying，LPV)[4]是一种常用于被控对象复杂的方法，它将系统用凸多面体表示，利用参数的变化切换控制器.这种切换思想则在20世纪90年代被Martensson[5]和Morse[6]等人引入到多模型自适应控制中，由于其良好的控制性能，多模型切换控制便在多模型自适应领域中作为主流思想，不断被后人应用.多模型切换控制[7]是基于性能指标切换函数选择最优模型，将该模型对应的控制器作为当前控制器实现稳定控制[8-9].近年来，多模型切换控制在理论和应用上均有了较大的发展.例如，从单层切换机制发展至内外两层切换机制[10-11]，从独自应用到与智能优化算法[12-13]、神经网络[14-15]等结合应用，从正常工况系统到故障补偿系统[16-17]中的应用.不过，随着系统参数维度的增长以及不确定区域的增加，为保证控制性能，需要大量补充模型数量[3]，也因此造成控制器的频繁切换导致系统输出震荡.为此，文献[18]提出了自适应混合控制，通过将控制信号混合输出，避免了控制器间的频繁切，以保证系统平滑输出.文献[19]基于混合控制的思想，利用动态优化双估计器优化参数子集，加快了系统收敛速度.混合控制虽然解决了震荡问题，但对模型数量的要求却无法降低.为此，Narendra等[20-21]提出了多模型二阶段自适应方法，该方法利用了凸组合的思想，将多个模型的参数加权混合，以此参数设计控制器，在保证系统控制性能良好的前提下，大大地减少了模型数量.并表示二阶段自适应控制对于时不变或参数周期变化的系统[22]具有良好控制效果.为进一步提升系统性能，Yin等[23]在二阶段自适应的基础上，添加了少量模型，并以这些模型建立了多个凸集合库，利用切换机制以获取更加优良的控制效果.由于二阶段自适应控制中的自适应模型在控制末期会收敛至相同的单一模型，导致模型退化，失去了多模型的优越性.为此，Chen等[24]提出了一种改进的二阶段自适应控制方法.该方法首先建立多个自适应模型，利用二阶段思想设计控制器，在自适应模型参数均接近真值时，固定所有自适应模型，并基于这些模型设计控制器，这种方法对于一类参数跳变小的系统十分有效.相比之下，文献[25]提及的多模型切换调节算法对于由于参数不确定区域大而导致参数具有大跳变的系统同样有效，此算法通过建立多个固定模型和少量的自适应模型，利用切换机制切换至最优控制器.当最优模型选为固定模型时，将固定模型的参数赋给自适应模型，重新作为参数辨识的初始值，并实现自适应控制.但其缺点在于，若需快速准确实现控制目标，仍然需要较大的模型数量.

为此，本文针对一类被控对象过程参数不确定区域大且存在参数跳变的线性时变连续时间系统，提出了多模型切换动态调节控制算法，该算法在双切换机制的监督下，使上下两层模型协同工作，在保证系统快速稳定的同时，也解决了模型需求量大的问题.首先，根据不确定区域大小确定上层模型并设计相应的控制器，根据性能指标函数实时确定最优上层模型，并利用切换机制确定分配子区域;其次，以最优上层模型为中心，利用动态分配方法，在子区域内分配得到新的下层模型，设计相应的控制器，并利用性能指标选取最优下层模型;然后，比较下层模型和自适应模型，选取最优模型，并利用切换机制将最优控制器切入系统;最后，数值仿真以及故障卫星系统的结果表明，针对一类参数具有大跳变的时变系统，多模型切换动态调节控制算法比起多模型切换调节控制算法具有暂态误差更小，收敛更快的特性.

2 对象描述

考虑如下线性时变连续时间系统:

式中:xp(·)∈Rn，u(·)∈R，Ap(·)∈Rn×n，b∈Rn.Ap(·)和b的形式如下:

式中:Ap(t)为友矩阵;参数api(t)(i=1，2，···，n)未知，但可从可观测的状态变量xp(t)与控制量u(t)得到.设θp(t)=[ap1(t) ap2(t)··· apn(t)]T为参数向量，并假设其所位于的不确定区域较大且具体范围已知，即

对于控制矩阵b的表述与式(2)不同的线性系统，利用如下方法可转化为式(2)的形式.

将被控对象转化为传递函数表达形式，即

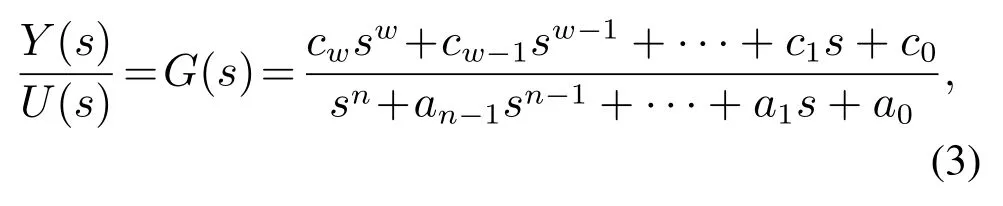
式中n为系统阶次且w ＜n.利用能控制标准型的转化方法，式(3)可表述为

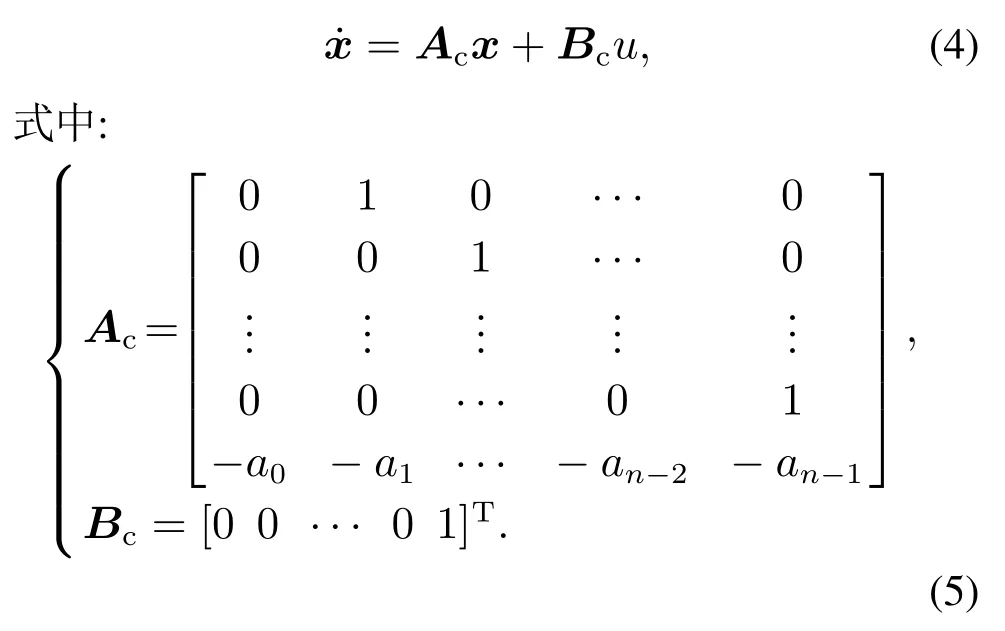
此时对象与式(2)描述一致.

最终控制目标是利用所设计的控制器u(t)，使被控对象的状态变量可以渐进地跟踪于参考状态变量，即使状态变量误差趋近于0.

3 多模型切换动态调节控制算法

3.1 自适应模型

根据上节中描述的控制目标，建立一稳定的参考模型表示如下:

式中r(·)∈R是已知的连续有界参考信号;系统矩阵Am与Ap(t)形式相同，其最后一行为参考模型的参数向量θm=[am1am2··· amn]T;参考状态向量xm可测.

为实现控制目标，需要利用被控对象参数设计控制器，但由于系统(1)参数未知，因此需利用系统状态估计实现参数辨识，对系统(1)做如下转换:

根据系统(7)，建立状态估计模型，

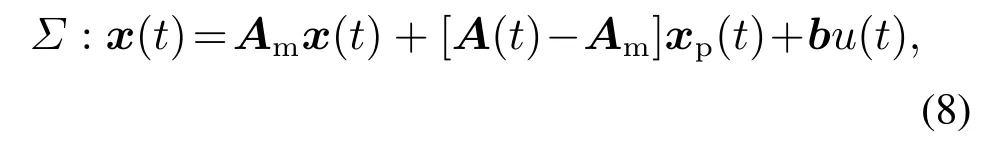
式中:A(t)与Ap(t)形式相同，其最后一行由参数辨识值θ(t)=[a1(t) a2(t)··· an(t)]T组成.参数辨识初始值θ(0)=[a1(0) a2(0)··· an(0)]T.

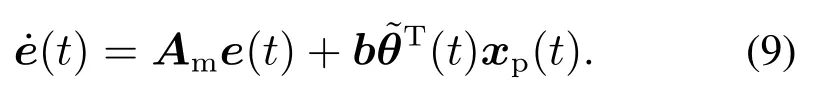
根据李雅普诺夫理论知，选取合适的李雅普诺夫方程函数可使参数辨识误差和状态估计误差均收敛于0，因此针对式(9)选取如下李雅普诺夫函数，即

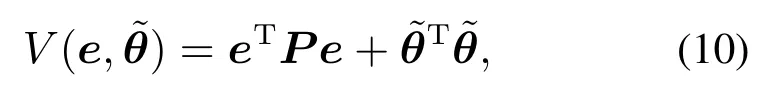
式中，P为使方程成立的对称正定矩阵.对式(10)求导得

为保证被控对象渐进跟踪参考模型，控制器的设计利用了模型参考自适应控制策略，即前馈反馈控制器

式中

设系统误差为ec(t)=xp(t)-xm(t).由式(6)-(7)和式(13)可得系统误差方程

为证明其收敛性，对式(15)作出如下变换:设k*=则式(15)可转化为

同理，根据李雅普诺夫理论，设李雅普诺夫函数为

引理1(Barbalat引理[26]) 对于函数g(t):R+→R，如果g(t)一致连续且存在且有界，那么

由于参考模型稳定，则xm有界，因此可知xp(t)=xm(t)+ec(t)有界，且有界，因此是一致有界的，即g(t)对时间t是一致连续的.由于V ≥0，且≤0，因此V(∞)存在.所以，

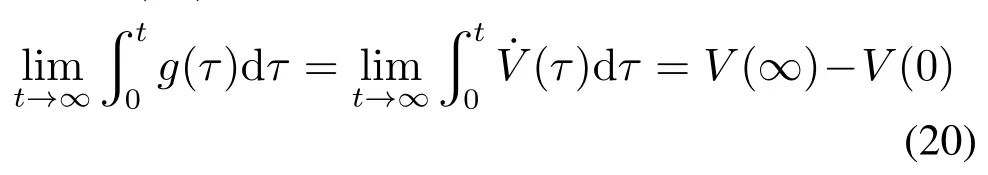
有界.由引理1，则有

3.2 多固定模型

已知N个固定模型的参数向量，建立N个固定模型即

式 中:xi(t0)=xp(t0)，i ∈Ω={1，2，···，N}，即N个固定模型和真实对象拥有相同的初始状态，Ai为友矩阵，其最后一行为固定模型的参数向量，即

针对每个固定模型设计相应的控制器，

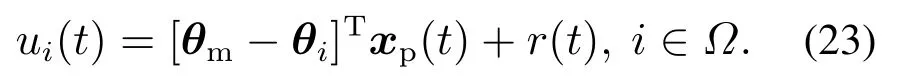
联立式(1)(23)得到

参数误差ei(t)=xi(t)-xp(t)满足

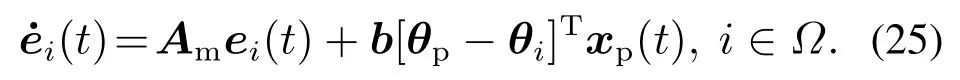
根据多模型自适应理论，在设计控制器时，可以采用切换策略控制系统，即利用切换策略对已设计的控制器集合选取最优控制器，切换至回路控制被控对象.然而，切换策略的不同会影响到系统的动态性能，因此切换策略的选择必须能够准确反映系统的过程.因此，切换策略的设计成为了一个关键性问题.根据本文对象特征，考虑下述性能指标:

式中α，β为常系数，分别侧重当前误差及过去累计误差，可按需求具体设计.

在任意时刻，当Jq(t)=min{Ji(t)}，可得控制器u(t)为

显然，当存在θi=θp时，控制性能最优.但由于系统参数θp未知，固定模型的参数选取十分关键，由于参数的不确定区域S已知，为此，可将参数不确定区域S划分为N个子集Si，i ∈Ω，且Si满足以下分配条件:

2) Sj∩Sk=∅，j，k ∈Ω，且j/=k;

3) 若∀θp∈Si，θi∈Si以及0 ＜r ＜∞满足

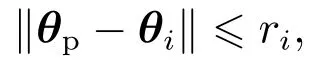
式中:θp为Si的中心值，即为固定模型的参数值;ri为第i个子集的半径.

上述分配条件也可称作模型的分配方法，其中条件1使子集覆盖不确定区域;条件2使子集间处处不重叠;条件3满足了固定模型的参数全部位于不确定区域中，若ri全部相等，则此时的分配方式为均匀分配.

3.3 动态分配固定模型

在多模型领域，动态分配是指根据实时数据、性能指标等对模型参数、数量等的实时修改与更新，以改善系统的暂态和稳态性能.

动态分配固定模型则是将N个固定模型按照上一节所述条件分配于不确定区域Sθ内，利用式(26)实时计算性能指标Ji(t).在时刻t1时，每个模型在此时刻的性能指标为Ji(t1)，并得到最优固定模型Mi.此时真实参数θp最接近θi，因此则认为真实参数θp位于模型Mi所在的子区域Si内.接着，以第i个模型Mi为中心，将其余N -1个模型Mj(j/=i)按照上一节所述的条件分配在子区域Si内，实现固定模型的动态分配.

如图1所示，9个模型按照均匀分配法的分配方法分布于不确定系统中，根据式(26)计算可得M3为最优模型.因此，其他8个模型都被均匀分配到以M3为中心的子区域S3内.

图1 模型的动态分配Fig.1 Dynamic allocation of models

虽然动态分配使得固定模型的参数发生变化，使得设计控制器时所需参数也发生了变化.但是，分配得到的模型为固定模型，可以利用第3.2节所述方法，根据性能指标选取最优模型继续设计控制器.

3.4 多模型切换动态调节控制算法

多模型切换动态调节控制算法由3部分组成，即多模型集、监督机制与控制器集.多模型集由4种模型组成，包括上层模型、下层模型、传统自适应模型以及可重新赋值的自适应模型.其中分布于整个不确定区域S内的N个固定模型称为上层模型，利用动态分配得到的N个模型称为下层模型.监督机制为双切换机制，即利用上层模型的性能指标切换分配子区域;利用下层模型的性能指标切换控制器.控制器集则是由上下层模型以及两个自适应模型的参数设计的控制器组成.算法的主要思想为:利用上层模型选取对象参数的子区域，并且不断监督以及时更新最优上层模型及子区域;利用动态分配得到的下层模型设计控制器，利用切换机制切换控制器以使得系统快速稳定的运行.根据第3.1节至第3.3节的内容，此算法需要整个系统满足如下几个条件:

1) 不确定区域S是已知的;

2) 在所有模型中，至少有一个模型的参数向量θi满足系统的稳定条件，即矩阵[Ap+b(θm-θi)T]的所有特征值实部均为负数;

3) 所选择的上层模型应当根据第3.2节中的分配方法分布在不确定区域内，且下层模型的分配方法也应满足上述分配方式.

多模型切换动态调节控制算法的具体流程可见图2所示的流程图.其步骤如下:

步骤1选取检测时间间隔ΔT以及分配层数f，然后根据不确定区域大小利用分配方式建立合适数量的N个上层模型Mi(i ∈Ω={1，2，···，N})，并一个传统自适应模型MN+1以及一个可重新赋值的自适应模型MN+2.

步骤2比较全部上层模型Mi以及模型MN+1，MN+2，利用性能指标确定最优模型，并根据切换机制切换至最优控制器.若最优模型为自适应模型MN+1，则使用式(12)继续进行参数辨识，控制器切换至自适应控制器;若最优模型为上层模型Mj，则将该模型参数赋予可重新赋值自适应模型MN+2的参数初值中，此时控制器切换至此参数设计的控制器;若最优模型为可重新赋值的自适应模型MN+2，利用模型参数值设计控制器并切换至系统中，并进行参数变数.

步骤3在经过一个检测时间间隔ΔT后，利用监督机制选取最优上层模型Mj后，利用动态分配方法分配N个下层模型在子区域Sj内，记为Oi(i ∈Ω)上层模型保持不变.并比较全部下层模型Oi(i ∈Ω)与模型MN+1，MN+2根据性能指标比较，选定最优模型并根据切换机制切换控制器.

步骤4在下一个检测时间间隔后，判断当前时刻的最优上层模型Mj是否与上一时刻的最优上层模型一致.若是，取当前最优下层模型为中心继续动态分配新的下层模型，舍弃先前的下层模型Oi(i ∈Ω)，并将新的下层模型记为Oi(i ∈Ω)，然后根据性能指标比较，选定最优模型，切换至最优控制器并进入步骤5.否则，舍弃所有下层模型，并返回至步骤2.

步骤5判断目前是否满足模型的分配层数n，若不满足，返回步骤4;若满足要求，进入步骤6.

步骤6持续根据切换机制选择最优控制器，并在下一个检测时间，判断当前时刻的最优上层模型Mj是否与上一检测时间的最优上层模型一致.若是，则返回步骤6;否则，舍弃所有下层模型Oi(i ∈Ω)，并返回至步骤2.

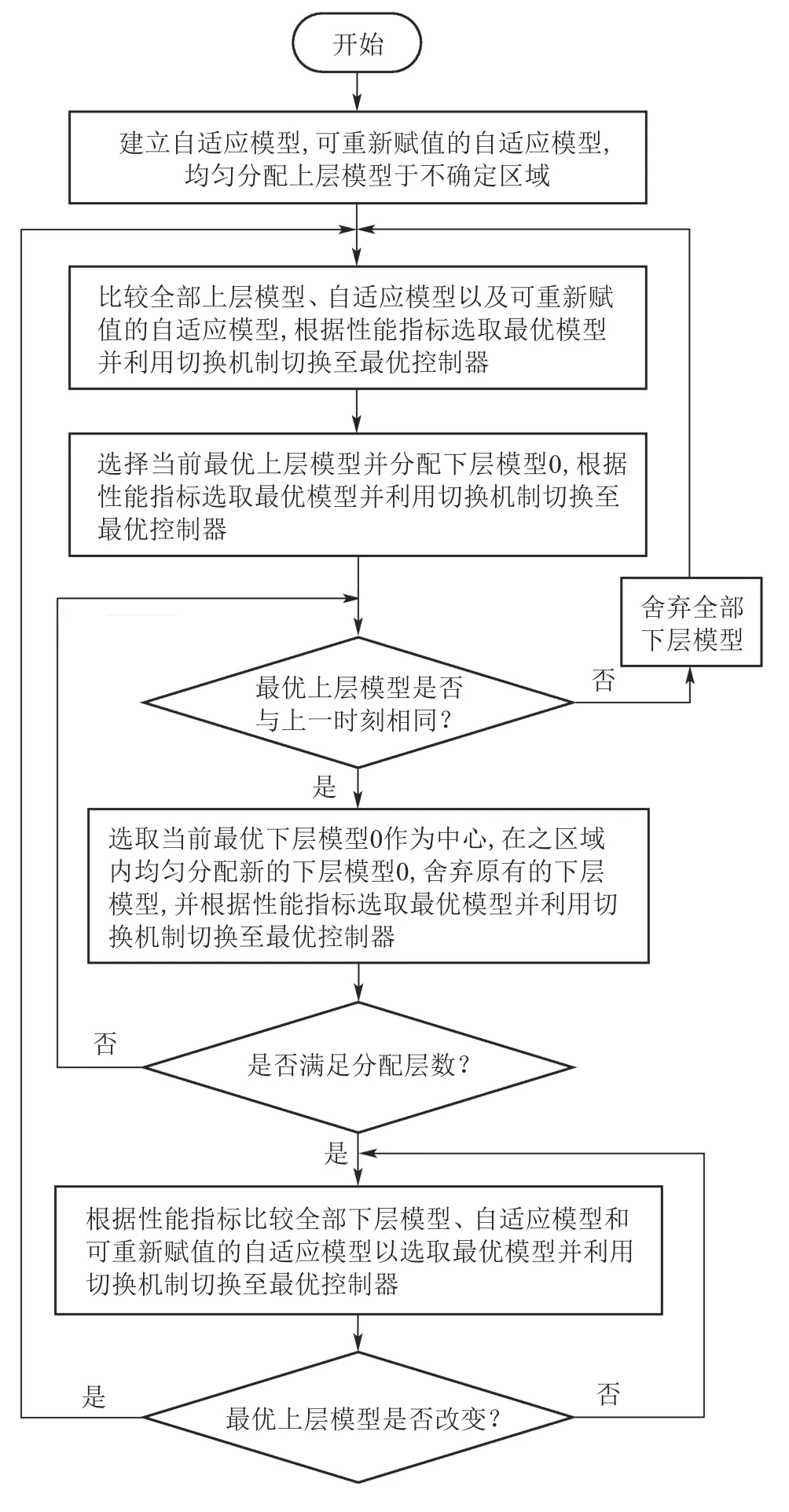
图2 算法流程Fig.2 Algorithm flow

时间间隔ΔT与分配层数f的选取规则:时间间隔可以先利用多固定模型控制算法先行测试，根据选取到最优模型的时间而定.分配层数f可以选择为无穷大，但实际上仅需几层即可，若当前下层模型的参数向量满足

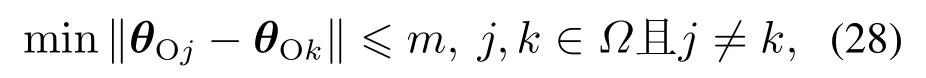
式中m为一常数，可根据实际需求选取.

由算法步骤可知，最初的N个上层模型Mi始终被监督机制监督，利用性能指标计算最优模型，选取子区域，若最优上层模型发生变化，则动态分配得到的下层模型所在的子区域直接发生变化，前期所分配得到的下层模型全部会被舍弃，这样做的原因如下:

1) 若出现由噪声或其他因素引起的辨识误差过大，导致上层模型选取暂时有误的情况，此算法能够有效的在错误消除后找到真正最优上层模型;

2) 上层模型可以快速地对参数发生大跳变的情况做出反应，以快速切换控制器，可以有效提高系统的快速性;

3) 模型个数增加N个，但是在控制效果上和N2个模型的多模型切换调节算法控制效果相似.也就是说，多模型切换动态调节算法和多模型切换调节控制算法在增加相同个数的模型时，前者体现出更好的控制效果.

4 对象描述

4.1 数值仿真研究

设某二维线性时变连续时间系统的参数向量满足

参考模型为极点是-2和-3的稳定模型，其参数向量为θm=[-6 -5]T，不确定区域较大但具体范围是已知的，设S=S=[-40 40]×[-40 40]∈R2.根据不确定区域的选取，以均匀分配的方式选取9个固定模型并将S划分为9个子区域，性能指标选择式(26)，分配层数f=2，自适应模型初值θ(0)=θ1.

图3所示的为9模型切换调节控制的系统响应图，虽然系统可以选定与被控对象参数相近的固定模型，可由于不确定区域较大，导致辨识模型追踪时间较长，调节时间过久，即使最终收敛，但性能较差.

图3 9模型切换调节算法的响应曲线Fig.3 Response curve of 9 models switching and tuning algorithm

图4所示的是多模型切换动态调节算法的系统响应图，图中表明，系统在经过动态分配后，系统响应明显优于多模型切换调节算法.图5所示的是两算法调节误差对比图，在应用本文算法后，跳变前调节时间从40 s缩短至20 s，跳变后调节时间从50 s缩短至20 s左右.

图4 多模型切换动态调节的响应曲线Fig.4 Response curve of multiple models switching and dynamic tuning algorithm

图5 9模型切换调节算法误差对比图Fig.5 9 models switching and tuning algorithm error comparison chart

由于上述仿真中，多模型切换调节算法只使用9个固定模型，但本文算法却使用18个固定模型，因此，为保证模型数量上的公平，采用18个固定模型的多模型切换调节算法作对比.如图6所示，即使模型数量相同，本文算法在暂态上表现了优越性.

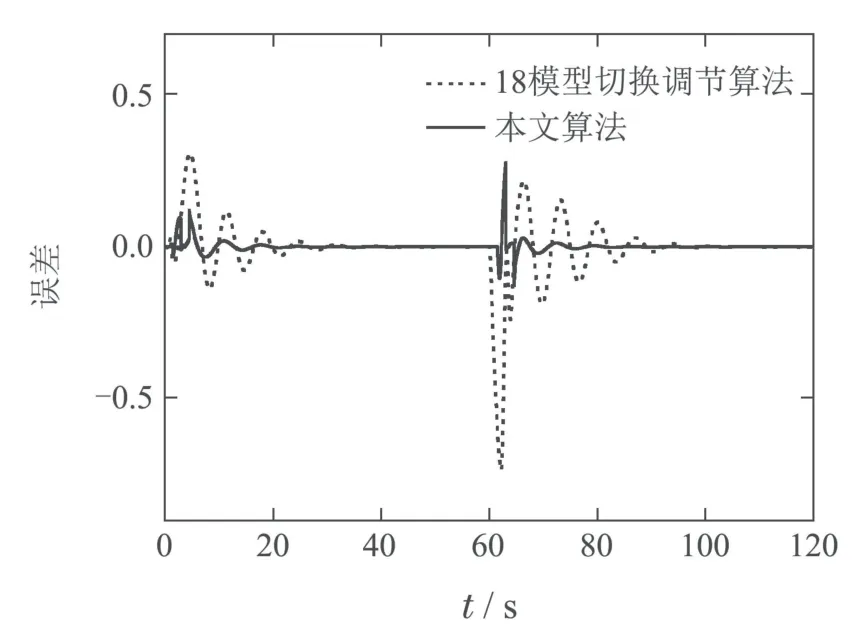
图6 18模型切换调节算法误差对比图Fig.6 18 models switching and tuning algorithm error comparison chart

图7所示的是使用81个模型的多模型切换调节算法和本算法的对比，此时前者模型数量大大增加，虽然跳变前性能相似，但跳变后的性能还是不及本文算法.

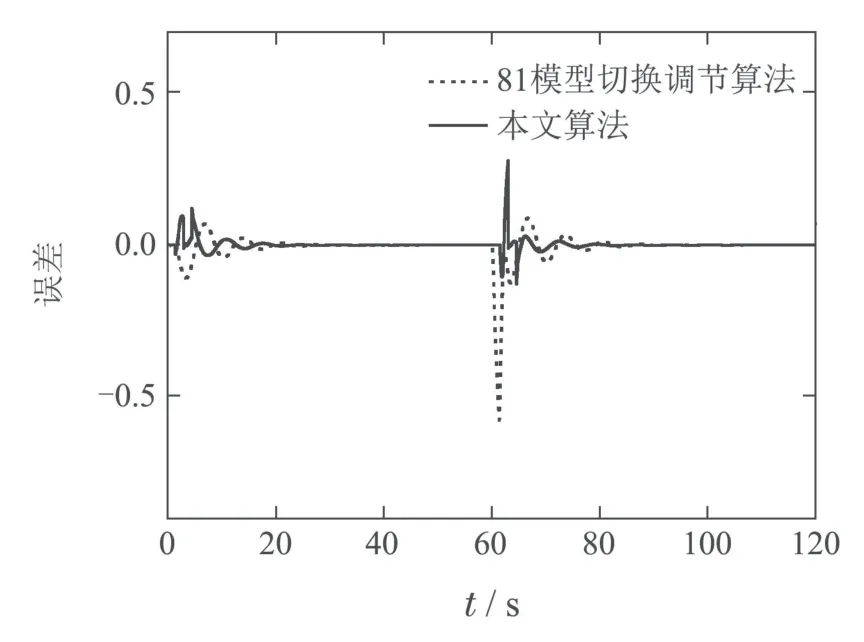
图7 81模型切换调节算法误差对比图Fig.7 81 models switching and tuning algorithm error comparison chart

根据以上仿真可以充分说明，在模型数量一致时，多模型切换动态调节算法比起多模型切换调节算法，其在快速性和暂态性能方面都表现出了更优越的结果.而在控制性能相似时，本文算法模型数量则少于多模型切换调节算法.

4.2 故障卫星仿真研究

为体现多模型切换动态调节算法的实际应用价值，考虑在圆轨道运行的卫星近距离相对运动模型[27]:

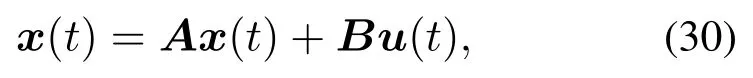
其中系统参数A，B分别为

式中ω为卫星的角速度.

状态变量x=Δx，Δy，Δz 分别表示卫星3 个方向的相对距离，u(t)=[u1(t) u2(t) u3(t)]T为3个执行器.从式(30)-(31)可知，x3=Δz仅由u3控制，因此在只考虑Δz的情况下，系统(30)可转化为

考虑执行器u1或u2发生故障的情况，故障类型考虑为跳变故障，即执行器提供小于非故障时且恒定的推力，此时造成卫星相对位置发生变化，因此轨道半径同时变化.根据卫星速度与轨道半径的关系，角速度发生变化，因此系统(32)参数发生跳变，所以为了解决故障卫星的参数跳变问题，采用多模型切换动态调节算法以验证算法的实用性，并与多模型切换调节算法作对比以验证算法的优越性.

系统在发生跳变前的角速度为ω1=6.3 rad/d，故障时刻为60 s，受故障影响后的速度为ω2=5 rad/d，因此系统的参数可表示为

其不确定区域S=[-45 0]×[-20 -25]∈R2，以均匀分配方法选取9个固定模型并划分S为9个子区域，9个固定模型的参数向量为

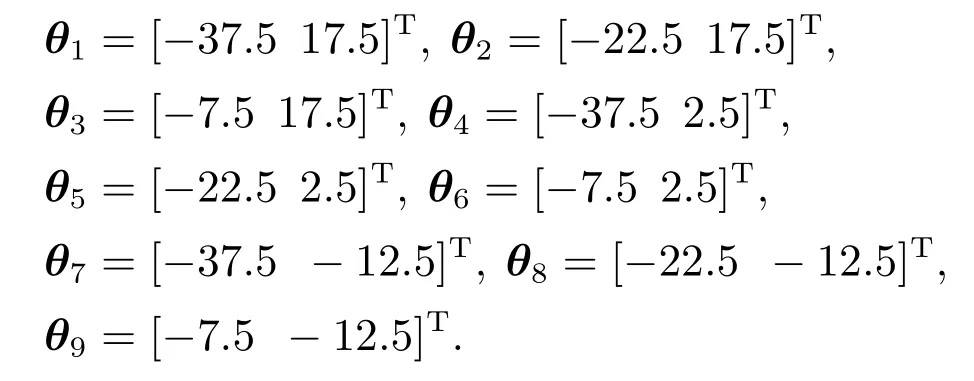
检测时间ΔT=1.5 s，分配层数f=2，自适应模型初值θ(0)=θ1.

利用两算法对故障卫星系统的参数路径、控制响应曲线以及控制误差如图8-14.

图8 故障卫星系统9模型切换调节算法的参数路径Fig.8 Parameter path of 9 models switching and tuning algorithm for the faulty satellite system

结果表明，对于故障卫星系统，跳变前的调节时间从50 s缩短至20 s，调变后的调节时间从50 s左右缩短至25 s左右，且系统误差有了明显的降低.

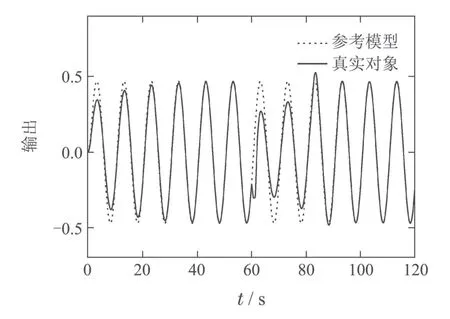
图9 故障卫星系统9模型切换调节算法的响应曲线Fig.9 Response curve of 9 models switching and tuning algorithm for the faulty satellite system

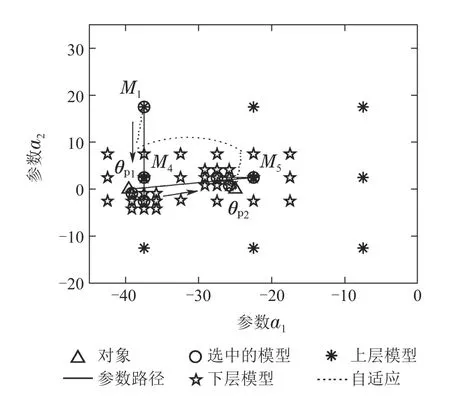
图10 故障卫星系统在本文算法下的参数路径Fig.10 Parameter path of faulty satellite system under this algorithm

图11 参数路径放大图1Fig.11 Enlarged parameter path 1

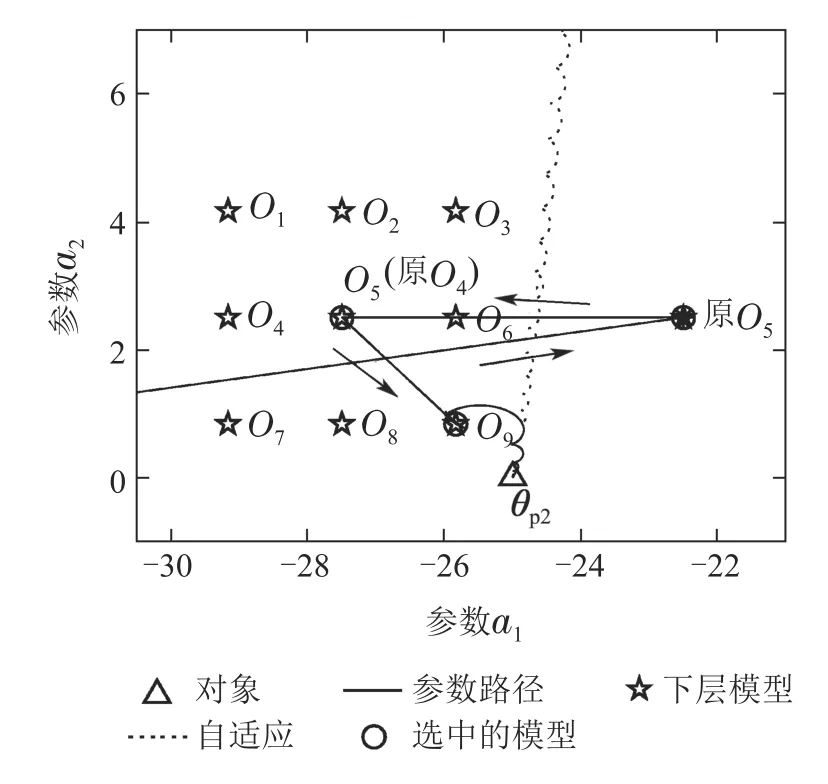
图12 参数路径放大图2Fig.12 Enlarged parameter path 2

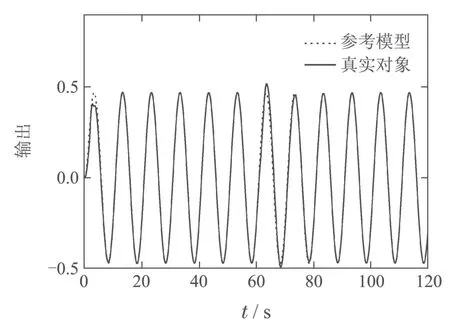
图13 故障卫星系统在本文算法下的响应曲线Fig.13 Response curve of faulty satellite system under this algorithm

图14 故障卫星系统9模型切换调节算法误差对比图Fig.14 Error comparison chart of 9 models switching and tuning algorithm for faulty satellite system

图15-16分别是18模型和81模型的多模型切换调节算法的结果，结果显示，即使模型数量增加，多模型切换调节算法也不及本文算法.因此，多模型切换动态调节算法对比于多模型切换调节算法在暂态误差和快速性等方面均有了提升.

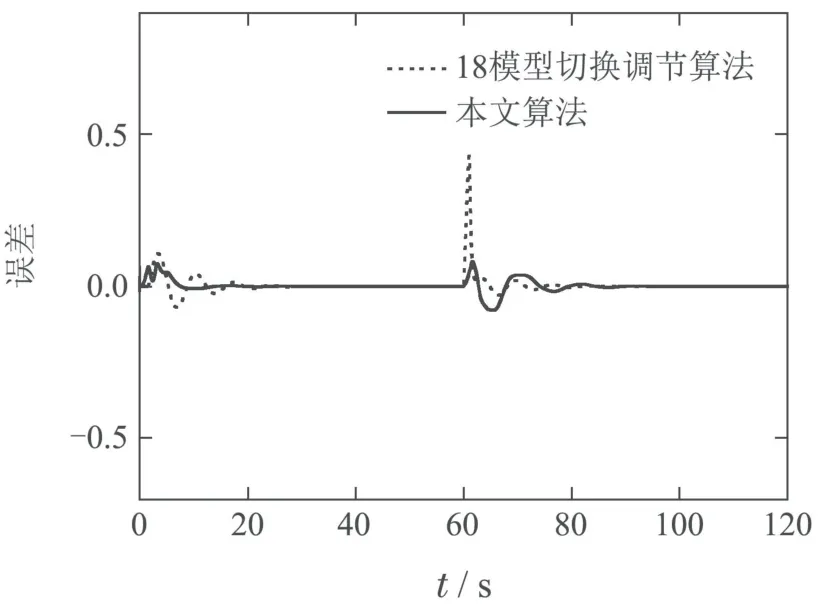
图15 故障卫星系统18模型切换调节算法误差对比图Fig.15 Error comparison chart of 18 models switching and tuning algorithm for faulty satellite system

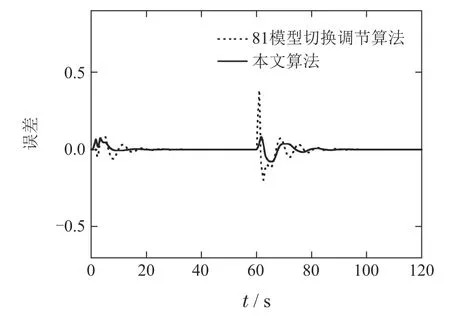
图16 故障卫星系统81模型切换调节算法误差对比图Fig.16 Error comparison chart of 81 models switching and tuning algorithm for faulty satellite system

5 结语

本文针对一类被控对象参数跳变大的线性时变单输入单输出连续时间系统提出一种新的控制算法，由于传统的多模型切换调节控制算法在面临大不确定区域的被控对象时，往往需要增加大量的模型才能更好的实现控制.因此，新的控制算法引入双切换机制，使上下层模型配合工作，使在加入了少量模型后的控制性能可以和多模型切换调节算法加入大量模型后的控制性能媲美，甚至可能会好于后者.根据最后数值和故障卫星的仿真结果表明，当系统参数不确定区域较大且存在参数跳变时，本文提出的多模型切换动态调节控制算法可以在增加的模型数量不多的情况下可以在系统暂态性能上实现有效的提升.