垂直三连杆欠驱动机械臂通用控制策略设计

王乐君，孟庆鑫，赖旭芝，吴 敏

(中国地质大学(武汉)自动化学院，湖北武汉 430074;复杂系统先进控制与智能自动化湖北省重点实验室，湖北武汉 430074)

1 引言

欠驱动系统[1-2]是一类控制输入维数小于自由度维数的非线性系统，该类系统在节能、降低成本、减轻重量和增强系统灵活度等方面具有一定优势.然而，该类系统动力学特性比较复杂，系统状态间存在强耦合和非线性关系.由于部分驱动关节的缺失，该类系统的控制存在巨大的挑战.因此，对欠驱动系统的研究具有重要的实用价值和理论意义.

垂直欠驱动机械臂[3-4]是一类典型的欠驱动系统，此类系统的控制目标通常是将机械臂末端点从垂直向下的初始位置开始移动，并最终将其稳定在垂直向上的目标位置[5-6].垂直欠驱动机械臂属于二阶非完整系统[7]，系统连杆间存在角加速度约束，不满足Brockett条件[8]，很难通过一个光滑的控制器实现系统的控制目标.但由于该类系统在垂直向上目标位置附近线性近似模型可控，因此学者们通常利用分区控制的方法[9-10]将系统运动空间划分为摇起区和平衡区，进而实现系统的控制目标.

然而，分区控制方法存在以下问题:1)无法从理论上来精确地划分摇起区和平衡区的范围.当平衡区范围划分得较窄时，会导致切换条件很难满足[11];而当平衡区范围划分得较大时，在切换点处线性近似模型存在较大误差，因此切换时会出现力矩突变[12-13]，从而使平衡控制器很难将系统稳定到目标位置;2)摇起运动控制过程中，由于系统状态之间复杂的耦合关系，常用的摇起控制易出现奇异现象.尽管部分学者通过调整控制器参数可以规避奇异问题[14]，但这会增加控制器设计难度.另外，现有的垂直欠驱动机械臂的各种控制方法只能实现特定结构系统的控制目标[15-16]，缺少对这类系统通用控制方法的研究.

为解决上述问题，本文针对含单一欠驱动关节的垂直三连杆欠驱动机械臂，提出一种基于振荡衰减轨迹的通用控制策略，该控制策略无需分区即可实现系统的控制目标.首先，根据驱动连杆的初始和目标状态，为驱动连杆规划含可调参数的振荡衰减轨迹，该轨迹能确保驱动连杆在一定时间内由初始状态运动到目标状态.同时，基于连杆状态间存在的耦合关系，引入粒子群优化算法优化驱动连杆轨迹的参数，确保欠驱动连杆和驱动连杆在相同时刻运动至目标状态.设计轨迹跟踪控制器使驱动连杆跟踪优化后的轨迹，则机械臂末端点由垂直向下初始位置运动至垂直向上目标位置.进而设计镇定控制器将末端点稳定在目标位置.最后，通过仿真实验证明所提方法的有效性.

本文的创新点如下:

1) 所提基于振荡衰减轨迹的控制策略无需对系统运动空间进行划分即可实现系统的控制目标;

2) 所提轨迹规划与跟踪控制方法可以有效规避运动过程中控制器的奇异现象，简化控制器设计;

3) 所提控制策略是一种通用控制策略，对含单一欠驱动关节的垂直三连杆欠驱动机械臂中的三类系统均有效.

2 系统动力学模型

图1为垂直三连杆全驱动机械臂示意图.其中:mr，Lr，Ir分别代表机械臂第r连杆的质量、长度和转动惯量;lr为第r连杆质心到前一关节的长度;ur为系统控制力矩;r=1，2，3.

图1 垂直三连杆全驱动机械臂模型Fig.1 The model of vertical three-link full-actuated manipulators

由欧拉-拉格朗日方程可得三连杆垂直全驱动机械臂的动力学模型为

当第j(j ∈{1，2，3})关节缺少驱动装置时，上述全驱动系统变成欠驱动系统，uj=0.记机械臂第i关节为驱动关节，i ∈{c1，c2}⊆{1，2，3}{j}.由式(1)可得驱动连杆和欠驱动连杆状态量之间的耦合关系为

其中Mj，Hj和Gj分别为和G(q)的第j行.

根据欠驱动关节位置的不同，可将含单一欠驱动关节的垂直三连杆欠驱动机械臂分为3类:1)PAA系统(j=1);2)APA系统(j=2);3)AAP系统(j=3).其中:A代表驱动关节，P代表欠驱动关节.

记x1=x=式(1)可写为如下状态方程的形式:

其中:

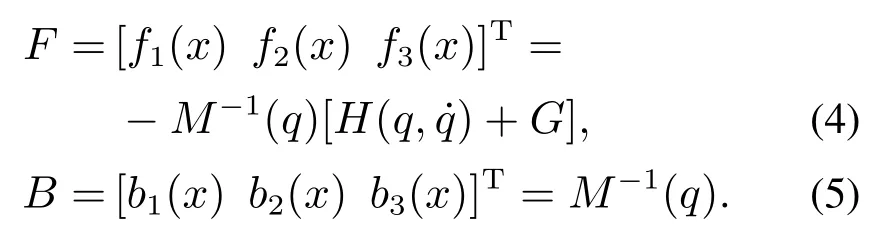
3 轨迹规划

本节针对驱动连杆设计振荡衰减轨迹，该轨迹能够保证驱动连杆在一定时间运动到目标状态.然后，基于连杆状态间的耦合关系，通过粒子群优化算法优化驱动连杆轨迹参数，使欠驱动连杆在相同时间内运动至目标状态.

3.1 驱动连杆振荡衰减轨迹设计

其中:qis和qif分别为驱动连杆的初始角度和目标角度;ki1和ki2为可调节的轨迹参数且0 ＜ki1＜1，ki2＞0.

对式(6)求导可得

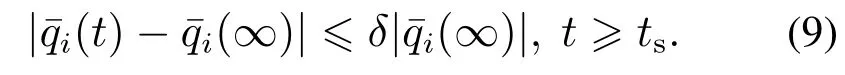
图2 轨迹的示意图Fig.2 Schematic diagram of the trajectory

结合式(6)，可得

则在t ≥ts2时，第c2根驱动连杆运动至目标状态.为保证在相同时间内两根驱动连杆均运动至目标状态，将最终调节时间ts取为

此时，驱动连杆运动至目标状态，即

式(2)为连杆状态间的耦合关系.根据这一耦合关系，本文发现，当驱动连杆的运动状态改变时，欠驱动连杆的运动状态也随之改变.由式(7)-(8)可知，驱动连杆的运动状态随轨迹参数ki1和ki2而变化.因此，通过改变ki1和ki2可以间接调节欠驱动连杆在ts时刻的状态量.接下来需选择合适ki1和ki2使欠驱动连杆在ts时刻也运动至其目标状态，即

下一小节中，引入粒子群优化算法优化轨迹参数，从而使欠驱动连杆在相同调节时间内运动至目标状态，即保证式(17)成立.

3.2 轨迹参数优化

为保证式(17)成立，本节通过粒子群优化算法优化轨迹参数ki1和ki2.结合欠驱动连杆目标状态和ts时刻欠驱动连杆状态量，定义评价函数为

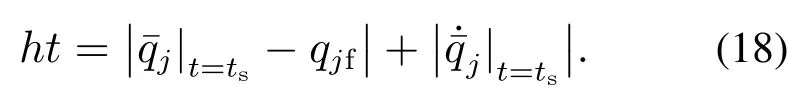
粒子群算法流程如下:

算法1轨迹参数优化.

参数初始化:gen=0，随机初始化粒子群;

循环程序:

通过粒子群算法得到一组优化参数ki1和ki2，将其代入到式(6)中，即可得到优化后的驱动连杆轨迹.当t=ts时，驱动连杆沿优化后的轨迹运动至目标状态，同时欠驱动连杆也运动至目标状态，即

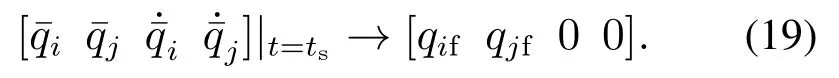
此时，根据驱动连杆和欠驱动连杆状态量的变化，系统末端点由垂直向下初始位置运动至垂直向上的目标位置.

4 控制器设计

基于优化后的振荡衰减轨迹，利用滑模方法设计跟踪控制器使系统末端点从垂直向下初始位置移动到垂直向上目标位置;同时，利用极点配置方法设计镇定控制器克服重力作用将末端点稳定在垂直向上目标位置.

4.1 跟踪控制器设计

利用滑模方法设计跟踪控制器.设计滑模面Si:

然而，机械臂末端点受重力作用很难稳定在垂直向上目标位置.因此，本文进一步设计镇定控制器实现系统的稳定控制.

4.2 镇定控制器设计

本节利用极点配置方法设计镇定控制器克服重力作用，将末端点稳定在垂直向上目标位置.

在目标位置处对式(3)进行近似线性化，得到

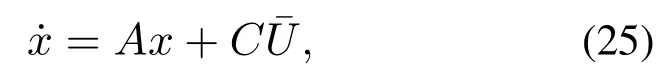
根据A和C的表达式，可以计算出

说明线性近似模型(25)是可控的.

设计镇定控制器uis为

其中K为增益矩阵.

将式(27)代入式(25)中，可得

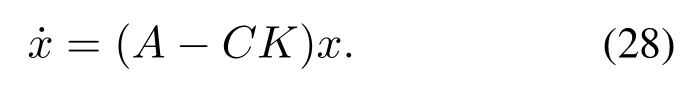
通过极点配置方法，并借助MATLAB中PLACE命令求得K，使(A-CK)的特征根位于坐标轴虚轴左半平面，从而保证系统末端点稳定在垂直向上目标位置.

综上所述，本文将控制器切换条件设计为t ≥ts.基于此，将控制过程分为轨迹跟踪控制和镇定控制两个阶段.当0 ≤t ＜ts时，ui=uit，通过轨迹跟踪控制，系统末端点运动至目标位置;当t ≥ts时，ui=uis，末端点在镇定控制器作用下稳定在垂直向上目标位置.

5 仿真实验及分析

本节通过3组仿真实验验证所提控制策略的有效性.选择如下3连杆垂直欠驱动机械臂模型参数进行仿真:

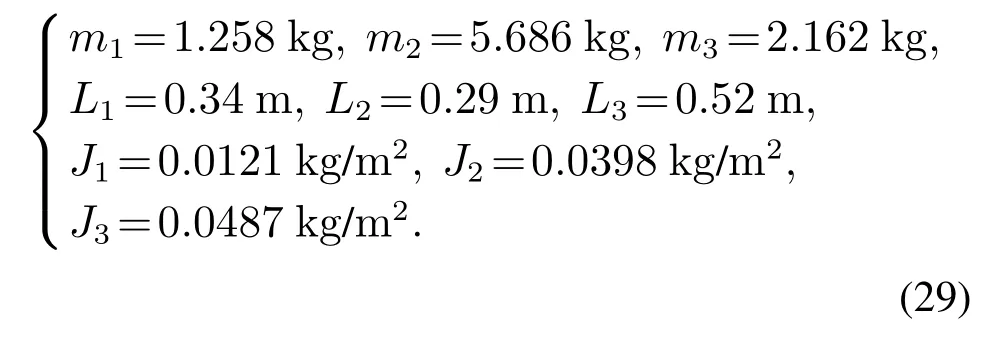
将控制器(23)(27)及粒子群算法中参数取为

5.1 PAA系统仿真

将驱动连杆初始角度和目标角度分别取为

控制器(23)(27)及粒子群算法中各参数如式(30).根据式(29)-(31)，通过粒子群算法可求得

因此ts=3.2379 s.

将期望的极点选择为-2，-3，-4，-4，-5，-6.利用MATLAB中PLACE命令求得K为

仿真结果如图3.当t ≤ts=3.2379 s时，在跟踪控制器(23)作用下收敛到[2π 2π 2π 0 0 0]，系统末端点从垂直向下初始位置运动到垂直向上目标位置.同时力矩收敛为零.当t＞3.2379 s时，控制器由跟踪控制器(23)切换至镇定控制器(27)，末端点在控制器(27)作用下稳定在垂直向上目标位置，从而实现控制目标.控制力矩保持在[-58.8035，76.3107]N·m范围内，整个控制过程中未出现力矩突变.与文献[16]中方法和控制效果进行比较，本文方法设计简单，计算量小，而且控制时间显著缩短，整个控制过程更加平滑.

图3 PAA系统仿真结果Fig.3 The simulation results for the PAA

5.2 APA系统仿真

将驱动连杆初始角度和目标角度取为

控制器(23)(27)及粒子群算法中各参数如式(30).根据式(29)-(30)和式(34).通过粒子群算法可求得

因此ts=2.4355 s.

选择相同极点，求得增益矩阵K为

图4为仿真结果:当t≤ts=2.4355 s时，通过跟踪控制，系统末端点运动到垂直向上目标位置.当t＞2.4355 s时，在控制器(27)作用下实现末端点在目标位置的稳定控制.本文方法在t=ts时各连杆状态量均收敛至目标状态，力矩收敛到零.因此，在控制器切换时没有产生力矩突变.

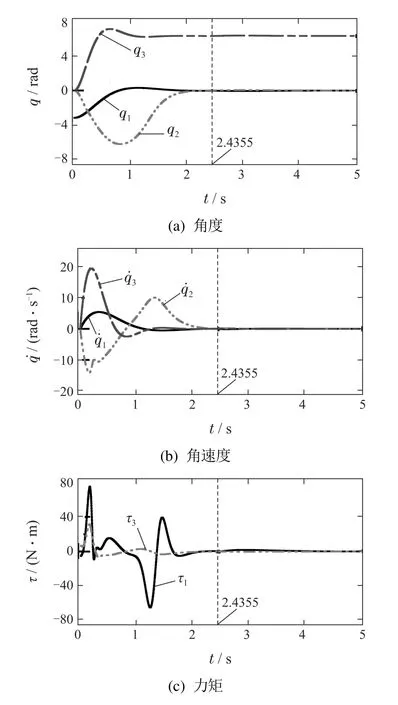
图4 APA系统仿真结Fig.4 The simulation results for the APA

5.3 AAP系统仿真

将驱动连杆初始角度和目标角度取为

控制器(23)(27)及粒子群优化算法中各参数如式(30).根据式(29)-(30)和式(37)，通过粒子群优化算法可求得

因此ts=10.3185 s.

用相同方法求得增益矩阵K为

仿真结果如图5所示.当t ≤ts=10.3185 s时，在跟踪控制器(23)作用下，

系统末端点运动到垂直向上目标位置.当t＞10.3185 s时，在镇定控制器(27)作用下，末端点稳定在垂直向上目标位置，实现控制目标.同样地，整个控制过程快速而且平滑.

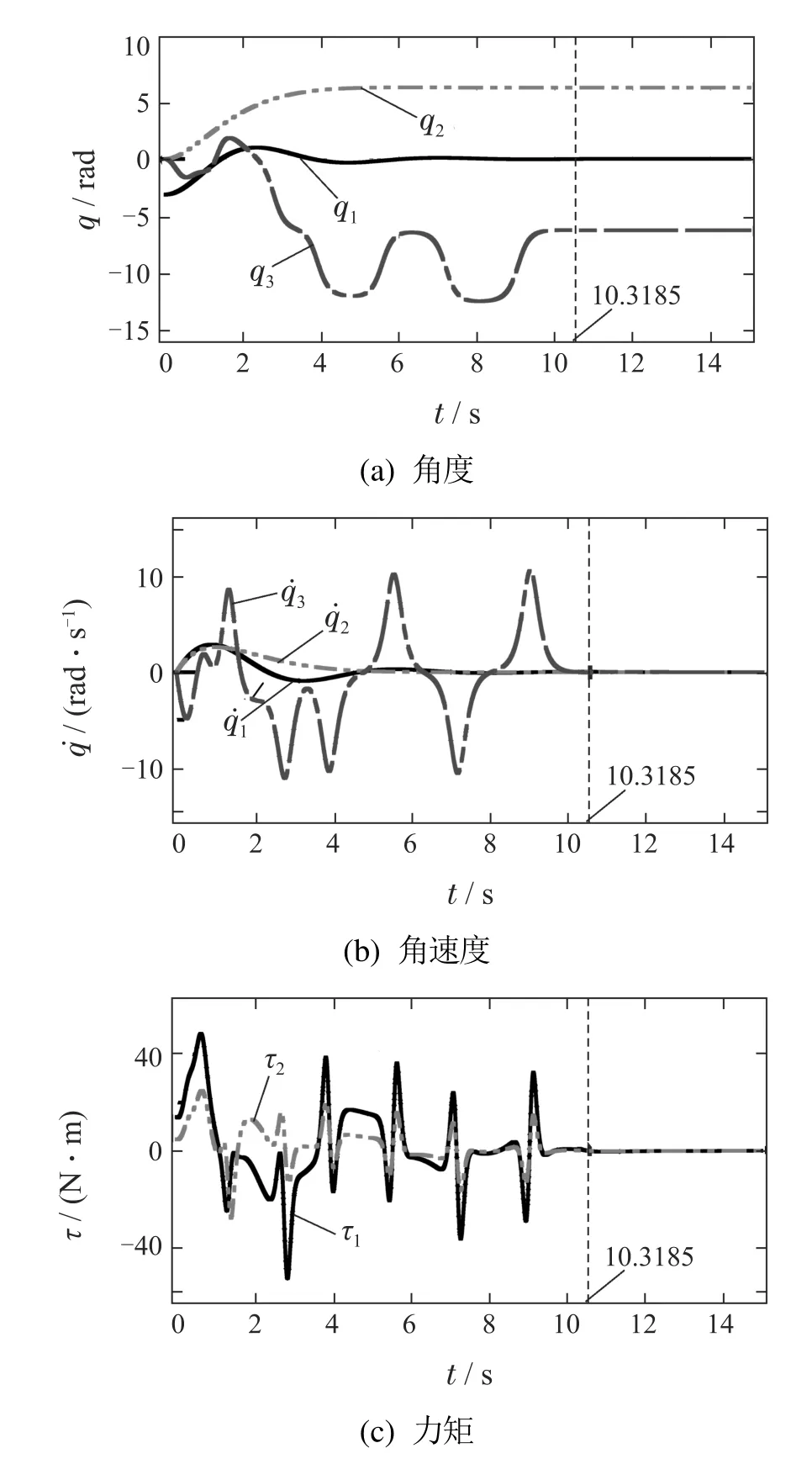
图5 AAP系统仿真结果Fig.5 The simulation results for the AAP

6 结论

本文针对含单一欠驱动关节的垂直三连杆欠驱动机械臂提出一种基于振荡衰减轨迹规划的通用控制策略，通过不分区的方式快速且平滑地实现系统控制目标.根据驱动连杆的初始和目标状态，为驱动连杆规划一条含可调参数的振荡衰减轨迹.所设计的轨迹可在一定调节时间内将驱动连杆由初始状态直接移动至目标状态.基于连杆状态间的耦合关系，通过粒子群优化算法优化轨迹参数使欠驱动连杆在相同调节时间内也运动至目标状态.接着通过设计跟踪控制器和镇定控制器实现系统的控制目标.最后，仿真实验验证所提控制策略的有效性.值得一提的是，本文方法能够有效规避运动过程中控制器的奇异问题，极大地简化控制器设计.另外，本文方法还可以推广至含单一欠驱动关节的n连杆(n ≥3)垂直欠驱动机械臂控制策略设计中.

附录

式中α1，α2，···，α6，β1，···，β3的表达式见文献[14].

C的具体表达式为

随着欠驱动关节位置的不同，C中元素的取值也不相同.

当系统为PAA系统时，

当系统为APA系统时，

当系统为AAP系统时，