基于改进高效偏最小二乘的质量相关故障诊断

孔祥玉，解 建，罗家宇，李 强

(火箭军工程大学导弹工程学院，陕西西安 710025)

1 引言

近年来，随着传感器技术的快速发展，一些复杂工业设备的数据采集变得更加便捷.然而，面对这些大型复杂设备和系统，对其进行故障诊断却变得十分困难.原因在于传统故障检测诊断方法大多是通过系统的物理模型来进行的，面对高度集成化和复杂化的系统对其建立物理模型严重影响了生产效率和成本.因此，基于数据驱动[1]的多元统计过程监控[2-3](multivariate statistical process monitoring，MSPM)方法因其不需要建立系统精确的物理模型逐渐成为了该领域的研究热点，并在实际生产中取得了很好的应用效果.传统的多元统计过程监控方法主要有主成分分析(principal component analysis，PCA)[4]，独立成分分析(independent component analysis，ICA)[5]和偏最小二乘(partial least squares，PLS)[6-7]，其中以PLS 算法的应用最为广泛.PLS算法在对过程变量执行空间分解时可以将过程变量分解为两部分:一部分与最终产品性能指标相关即主元空间(principal component space，PCS)，另一部分与最终产品性能指标无关即残差空间(residual space，RS).对于质量无关子空间，因为其包含的质量无关信息不会影响最终产品质量，其影响往往可以忽略不计.而通过对质量相关子空间的监控可以获得影响产品质量的过程变量信息，方便人们对系统进行故障检测和诊断，避免不必要的经济损失和安全风险.

PLS算法虽然在实际生产中取得了较好的应用效果，但是当系统中含有较多的质量无关信息时其性能明显下降.为了解决该问题，去除质量无关信息的影响，Trygg和Wold[8]首先提出了一种正交信号校正(orthogonal signal correction，OSC)的预处理方法，该方法在对PLS进行建模前剔除了过程变量中的质量无关信息，很好的解决了质量无关信息对质量相关故障监控的干扰.为了从根本上实现对过程变量的正交分解，Yin等人[9]提出了一种新的空间分解算法即改进的偏最小二乘算法(modified partial least squares，MPLS)，该方法通过计算过程变量与质量变量的正交关系对过程变量进行正交分解，从而在质量相关子空间中去除了正交信息，该方法明显提高了质量相关故障检测率并且避免了大量的迭代过程.虽然MPLS从根本上解决了质量无关信息的干扰，但是MPLS在计算过程中存在广义逆计算，这可能会导致过程变量中与质量相关的信息丢失.针对这一问题，Peng等人[10]提出了高效偏最小二乘(efficient partial least squares，EPLS)算法，该算法在MPLS的基础上对过程变量的残差子空间进行PCA分解，分别对残差子空间中的主成分及噪声进行监控，明显提高了质量相关故障的可检测性.然而，在实际操作中EPLS算法是基于一个近似的假设对过程变量进行与质量相关的正交分解，这使得分解得到的质量相关子空间中依然含有少量与质量无关的信息，对连续流水生产形式的工业过程造成较大影响.为此，Kong等人[11]提出了基于正交信号校正的高效偏最小二乘(orthogonal signal correction efficient partial least squares，OSC-EPLS)的质量相关故障检测方法，该方法利用OSC预处理算法处理过程变量后再使用EPLS算法进行空间分解，获得了更能反映产品关键性能指标的质量相关子空间，从而提高了质量相关故障的检测率.

为了能够在准确检测出系统的质量相关故障后及时排除故障，尽可能减少经济损失和人员伤亡，还必须对系统进行故障诊断，找出导致故障发生的原因并对故障变量进行定位.最常用的PLS故障诊断方法多为基于贡献图[12]的故障诊断方法，在实际应用中具有较好的性能，但是在无故障时的过程变量会造成故障检测指标的贡献值不均等，影响算法准确定位故障变量.为了解决上述问题，本文提出使用一种基于改进的高效偏最小二乘(improved efficient partial least squares，IEPLS)质量相关故障诊断方法，IEPLS算法旨在解决两方面问题:1)传统的EPLS和OSC-EPLS等故障检测算法对质量相关故障的检测率较低，且质量无关故障误报率较高;2)基于贡献图的故障诊断方法对故障指标定位时的贡献不均等，导致在故障诊断过程中对主要的故障变量贡献值低.

本文所提的IEPLS质量相关故障诊断方法的主要创新如下:1)针对EPLS和OSC-EPLS算法在对质量相关故障检测时检测率较低的问题，提出使用局部协方差矩阵与局部数据信息增量矩阵[13]的方法对EPLS的质量相关子空间设计新的统计量和控制限.IEPLS解决了质量相关故障检测率较低的问题，并在一定程度上保证了质量无关故障较低的误报率，提高了算法的整体性能;2)在新的统计量和控制限的基础上，提出在EPLS的质量相关子空间结合新息贡献率[13]技术对故障变量进行定位，并对比传统的基于贡献图的故障诊断方法.实验结果表明，本文所提的IEPLS质量相关故障诊断方法对质量相关故障的检测性能更好，且对故障变量的定位具有较好的准确性.

本文结构安排如下:第2节对标准PLS算法进行简要回顾;第3节介绍了EPLS及其扩展的质量相关故障检测方法;第4节提出了基于IEPLS的质量相关故障诊断方法;第5节结合田纳西伊士曼过程，验证了所提算法的性能;第6节对IEPLS算法进行了总结.

2 标准PLS

标准PLS算法[6]给出一对输入输出数据矩阵X和Y，X代表自变量，Y 是因变量，并分别具有如下形式:

其中:N代表的是采样数，m和l分别代表输入变量和输出变量的个数.将原始变量空间投影到一个不相关的潜因子空间

T是得分矩阵.由于得分矩阵T无法从输入X中直接获得，需要引入权重R=W(PTW)-1，由此可得到

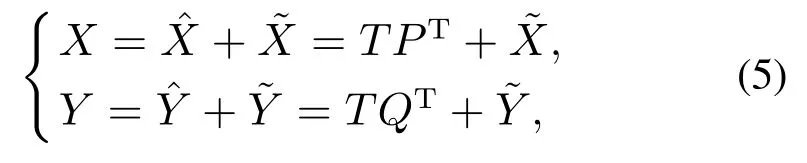
其中:A是主元个数，由交叉验证得到;P ∈Rm×A和Q ∈Rl×A分别是X和Y 的负载矩阵.PLS建模的各个参数使用非线性迭代偏最小二乘算法(nonlinear iterative partial least squares，NIPALS)[14]求得，在NIPALS迭代过程中，Y 的特征向量被用来回归X的特征向量，而X 的特征向量被用来对Y 进行回归.最终，算法通过旋转特征向量逐步提高相关性收敛获得模型参数.标准PLS求解模型参数的方法虽然存在计算量较大的问题，然而其最大缺点是对过程变量X使用了斜交分解导致了质量相关信息的丢失，从而造成了质量相关故障检测率较低，影响了其过程监控的性能.

3 EPLS及其扩展算法的过程监控技术

3.1 EPLS算法

由于标准PLS的上述缺点，人们相继提出了其他算法用来解决斜交分解问题.EPLS作为一种更为先进的故障检测算法，其应用效果要明显优于标准PLS及其扩展算法.EPLS算法首先给出了期望的输出变量Y 的分解如下:

基于式(6)和式(7)，推导出如下关系[10]:

那么，X和Y 之间的相关矩阵为

EPLS算法具体步骤如下:

1) 对建模数据中的输入X和输出Y 进行数据标准化;

2) 计算相关系数矩阵M:

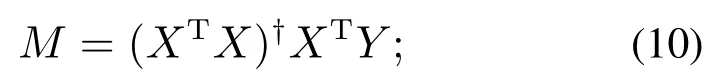
3) 利用式(11)对MMT执行奇异值分解(singular value decomposition，SVD)[15]:

4) 由上式获得参数求出两个正交投影算子如式(12)与式(13):

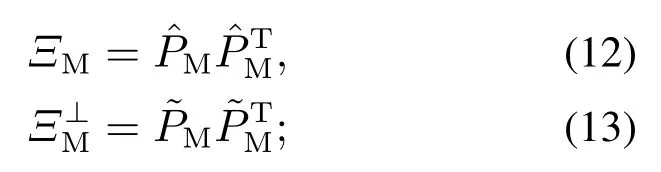
5) 当测试数据到来时，将X沿着正交投影算子分别向span{M}和span{M}⊥上投影后得到分解后的质量相关子空间和质量无关子空间

其中TXr和PXr分别是的得分矩阵和负载矩阵;

7) 得到最终的EPLS模型如下:

10) 结合上述设计的统计量和控制限与故障判据在相应空间进行故障检测.

由于Li 等人[17]提出的MPLS 算法对MMT使用SVD分解时可能会导致X中质量相关信息的丢失.因此，Peng等人[10]在分析了MPLS算法的这个不足之后，提出对残差子空间进行PCA分解，提高质量相关故障的检测率.如式(16)所示，作为主元子空间专门负责预测质量信息Y，而则代表输入中对预测输出无用的变量，其中是系统噪声.EPLS故障检测算法是在MPLS的基础上改进而来，不仅很好的解决对X斜交分解所产生的问题，同时使用SVD分解避免了大量的迭代过程，减少了算法的计算量.

3.2 OSC-EPLS算法

EPLS算法相比MPLS算法其质量相关故障检测精度得到了明显提升，然而EPLS算法的输入数据由于存在噪声干扰等情况导致其模型不能完全分解，其质量相关子空间仍然包含质量无关信息影响模型对质量信息的监测.因此Kong等将OSC算法引入到EPLS中，提出了基于4类OSC-EPLS模型过程监控技术，用来降低输入数据中与质量正交的信息.OSC预处理算法的详细步骤如下[11]:

1) 对正常数据中的输入X和输出Y 进行标准化处理;

2) 对X和Y 利用PLS迭代算法求出向量w和p;

3) 利用式(20)求出模型参数w⊥:

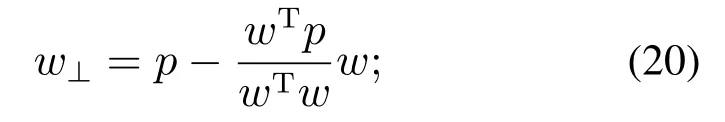
4) 利用式(21)计算正交得分向量t⊥:

5) 计算正交得分矩阵

6) 使用式(23)得出去正交后的输入矩阵Xosc:

7) 循环上述过程直至满足算法的收敛精度要求.

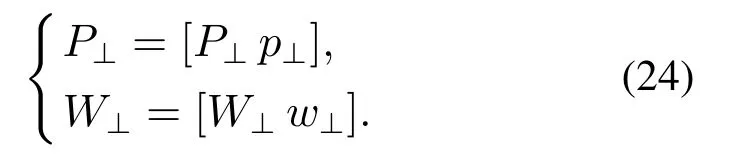
利用式(23)计算出的输入矩阵Xosc使用式(16)的EPLS模型进行空间分解，然后对质量相关空间和质量无关空间分别进行检测.本节主要介绍了基于(orthogonal projections to latent structures，OPLS)的正交信号预处理算法，其他3 种OSC 预处理算法如SWosc[18]，TFosc[19]和OPLS(PCA)的详细步骤见参考文献.

4 基于改进的高效偏最小二乘故障检测与辨识技术

本节设计了基于IEPLS的故障诊断方法，通过结合局部信息增量技术对现有EPLS算法的统计量和控制限进行改进，提高了现有算法的适应性和检测性能.另外，由于局部信息增量矩阵反映了相邻采样时刻之间新的信息差异，因此利用该思想可以定义局部信息增量矩阵为新息矩阵，利用新息矩阵计算新息贡献率对故障变量进行定位，从而实现IEPLS对质量相关故障的诊断.IEPLS算法的具体步骤如下所示:

Step 1对建模数据X和Y 进行标准化处理;

Step 2利用式(25)求取建模数据X和Y 的关系矩阵M:

Step 3利用式(26)对MMT进行SVD分解得到正交投影算子:

Step 4在观测数据前加入一段正常数据组成测试数据Xt并对其进行标准化处理;

Step 5将Xt向span{M}和span{M}⊥上正交分解得到式(29):

Step 6假设当前时刻为n，从正常数据选取长度为L的数据组成局部数据矩阵Xt，n;那么下一时刻的局部数据矩阵Xt，n+1为[13]

其中n′为正常数据中的某一时刻;

Step 7求两个时刻之间所形成的公共数据矩阵Gn，n+1，并定义局部信息增量均值gn，n+1为

其中IL-1=[1 1··· 1]∈R(L-1)×1.为了计算方便定 义Kn=Xt，n(Xt，n)T=Xt(n′-L+1)Xt(n′-L+1)T+

Step 8计算n时刻的局部协方差矩阵Rn:

Step 9类似Step 8，计算下一时刻的局部协方差矩阵Rn+1:

Step 10如式(36)计算局部信息增量矩阵Dn+1:

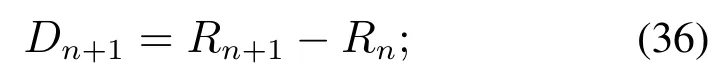
Step 11求取局部信息增量均值γn+1如式(37):

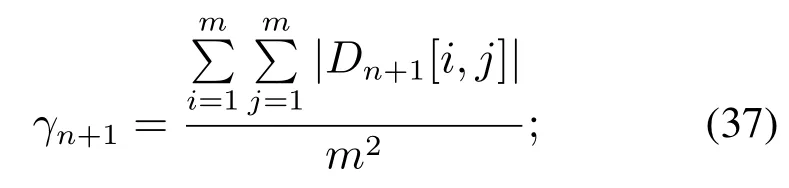
Step 12计算局部动态控制限σn+1如式(38):

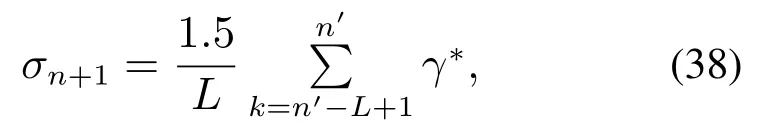
其中γ*为未发生故障的局部信息增量均值;

Step 13设计故障检测判据:

a) 当γn+1≥σn+1时，检测有质量相关故障发生;

b) 当γn+1＜σn+1时，检测无质量相关故障发生，继续故障检测;

Step 14利用新息矩阵Dn+1计算各变量的新息贡献率P(i)[13]如式(39)所示:

Step 15分析各个变量的新息贡献率得出故障诊断结果.

最后，本文所提的IEPLS算法步骤总结如下:

离线建模:

步骤1对建模数据进行预处理;

步骤2利用建模数据训练IEPLS模型;

步骤3获得IEPLS的模型参数.

在线检测:

步骤4对测试数据进行预处理;

步骤5利用IEPLS模型对测试数据进行空间分解;

步骤6利用设计的统计量和控制限进行故障检测;

故障判断:

步骤7利用新息贡献率诊断方法对故障空间进行故障诊断;

步骤8获得各个变量对故障的贡献结果进行故障变量定位.

注1需要进行说明的是式(38)设计的控制限中参数“1.5”为控制限的优化系数，在离线建模阶段通过对大量已知的正常工况数据使用粒子群(particle swarm optimization，PSO)智能优化算法训练得到的一个最优参数.因本文研究重点旨在提高算法的检测率和故障诊断性能，所以对于PSO算法本文不展开论述，具体计算方法见文献[14]和文献[20].

5 仿真实验与讨论

本节中使用田纳西伊士曼过程验证EPLS，OSCEPLS和IEPLS算法在故障检测与诊断中的性能，包括TEP实验参数初始化、基于IEPLS的故障检测方法和基于IEPLS的故障诊断方法3部分，实验结果表明所提算法的性能相比EPLS和OSC-EPLS有了明显提升.

5.1 TEP实验参数初始化

TEP是由美国田纳西伊士曼化工公司开发的一个工业模拟器[21-22]，该仿真被广泛用作连续过程的策略、监控和诊断的研究平台.田纳西伊士曼过程共包含4种反应物(A，C，D，E)，生成两种产物(G，H).另外，该过程还包含一种惰性物质B和副产物F，系统中的化学反应如下:

其中:g代表气体，lig代表液体.整个流程由5个操作单元组成，包括化学反应器、冷凝器、压缩机、汽/液分离器和分离器.TEP共包含22个数据集被用于故障检测与诊断等研究，该数据集由1个正常数据和21个特定的故障数据集组成.其中正常数据集共包含480个样本，而每个故障数据集共包含960个样本.在15个已知的故障数据集中又分为两种类型的故障数据，即质量相关故障IDV(3，4，9，11，14，15)和质量无关故障IDV(1，2，5-8，10，12，13).在本实验中，选取数据集中的22个过程变量XMEAS(1-22)和11个操纵变量XMV(1-11)作为输入X，选取过程变量XMEAS(35)作为质量变量y;另外，选取100个正常数据用来模拟系统在正常工作时所产生的采样数据，选取800个故障数据用来模拟系统在故障情况下产生的采样数据，二者共同组成测试数据集用来进行故障检测.实验参数初始化:选取主元个数A=15，由交叉验证所得;选取固定窗口长度L=5，由粒子群智能优化(PSO)算法寻优所得.实验共分为两部分，实验1通过TEP仿真实验对3种算法故障检测性能进行对比分析，并对所提算法的性能进行了验证总结;实验2则验证了所提算法的故障诊断性能，最后分析实验结果给出结论.

5.2 基于IEPLS的故障检测方法

为了验证故障5下质量变量y是否受到影响，采用Qy统计量[23]对输出y的残差空间进行直接监测，该Qy统计量定义如式(41)所示:

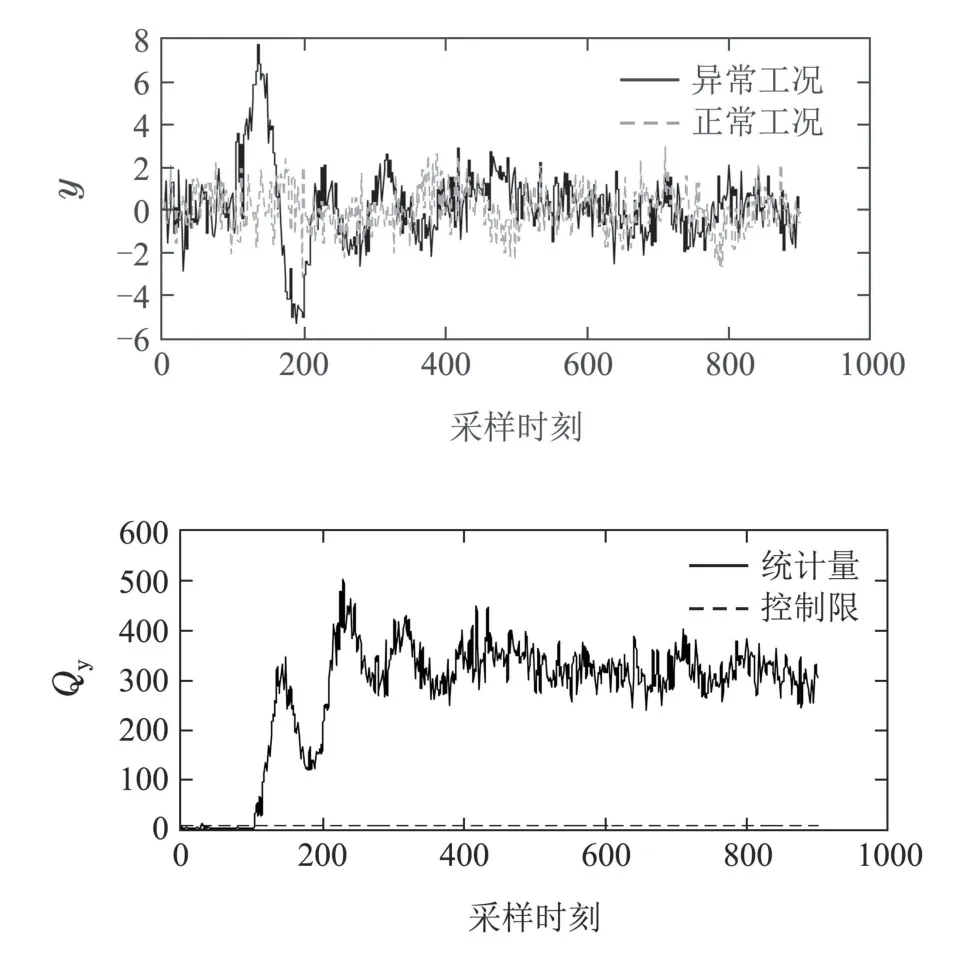
图1 IDV(5)下质量变量y的变化对比图Fig.1 Comparison chart of changes in quality variable y under IDV(5)

图2-4分别为3种算法的IDV(1)故障检测图，其中:实线部分为算法的统计量，虚线表示算法的控制限.3组实验各选取了900组数据，0～100区段为正常数据，100～900区段为故障数据，900～1000空白区段表示算法继续进行故障检测的一个实时过程.图2 为EPLS 算法的IDV(1)故障检测图，从图中可以看出EPLS算法在对IDV(1)进行检测时存在多处漏报情况，其检测率较低.图3是加入OSC预处理算法后的IDV(1)检测图，从图中可以看出OSC-EPLS算法在100～900 区段的漏报率相比于EPLS算法明显减少，证明OSC预处理算法提前去除了正交信息使得在进行质量相关信息检测时，其检测率明显提高，算法的整体性能得到了很大改善.

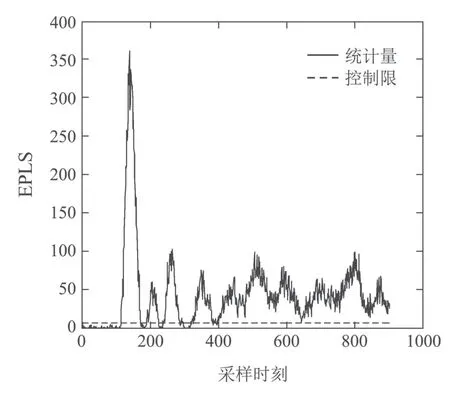
图2 EPLS的IDV(1)故障检测结果Fig.2 The IDV(1)fault detection result of EPLS

图3 OSC-EPLS的IDV(1)故障检测结果Fig.3 The IDV(1)fault detection result of OSC-EPLS

图4 IEPLS的IDV(1)故障检测结果Fig.4 The IDV(1)fault detection result of IEPLS

图4是所提的IEPLS算法的IDV(1)故障检测图，从图中可以看出，IEPLS设计的局部动态控制限在测试中当包含正常数据时可以准确根据正常数据特点而变化，其误报率大大降低;另一方面，在100～900故障数据区段IEPLS 的漏报率很低，质量相关故障均被IEPLS算法有效检测报警，相比EPLS和OSC-EPLS算法而言其质量相关故障检测性能有了很大提高.

图5是IEPLS对质量无关故障IDV(4)的检测结果，从图中可以看出在故障发生后，IEPLS的质量相关子空间没有检测到质量无关故障的发生;而在质量无关空间中，IEPLS算法准确检测出了质量无关故障的发生，验证了IEPLS检测质量无关故障的有效性.

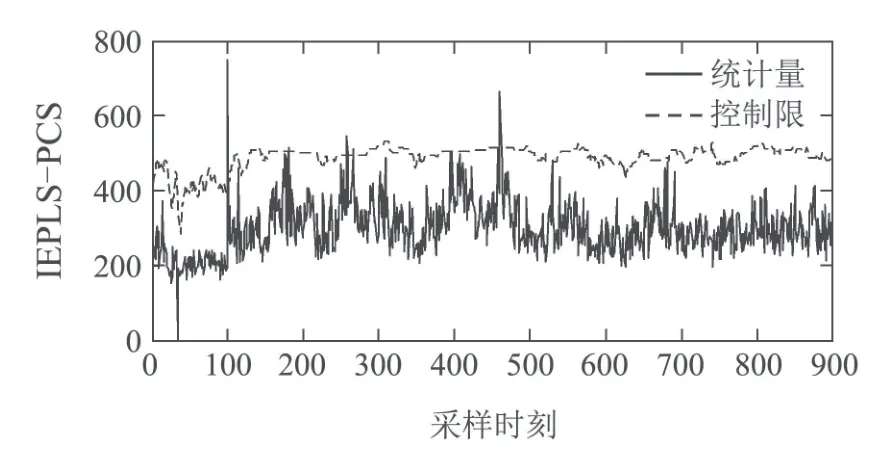
图5 IEPLS的IDV(4)故障检测结果Fig.5 The IDV(4)fault detection result of IEPLS

表1为3种算法所有质量相关故障的检测率.从表1中可以看出IEPLS对质量相关故障的检测性能明显优于EPLS和OSC-EPLS.表1中加粗部分为3种算法中检测率最高的一组，可以看出IEPLS 除了在IDV(5)算法的检测率低于OSC-EPLS算法以外，其余各组的质量相关故障检测率均高于EPLS和OSC-EPLS.其中，IEPLS算法的IDV(1)，IDV(6)对质量相关故障实现了100%监测报警.

表2中给出了3种算法的质量相关故障误报率，加粗部分为3 种算法中误报率最高的一组，可以看出EPLS算法和OSC-EPLS算法均存在较高的误报率.3种算法中OSC-EPLS算法的误报率较高，其中IDV(6)的质量相关故障误报率高达47.3%，可以看出OSCEPLS算法虽然提高了质量相关故障检测率，但是其质量相关故障误报率也明显提高.本文所提的IEPLS算法除了在IDV(5)算法的误报率高于EPLS和OSCEPLS算法0.9%以外，其余各组的质量相关故障误报率均低于EPLS或OSC-EPLS.最后，根据多次实验得出的实验数据可以看出本文所提的IEPLS算法的质量相关故障检测性能明显提高.

表1 TE过程中3种算法的质量相关故障检测率Table 1 Quality-related fault detection rate of three algorithms in TE process

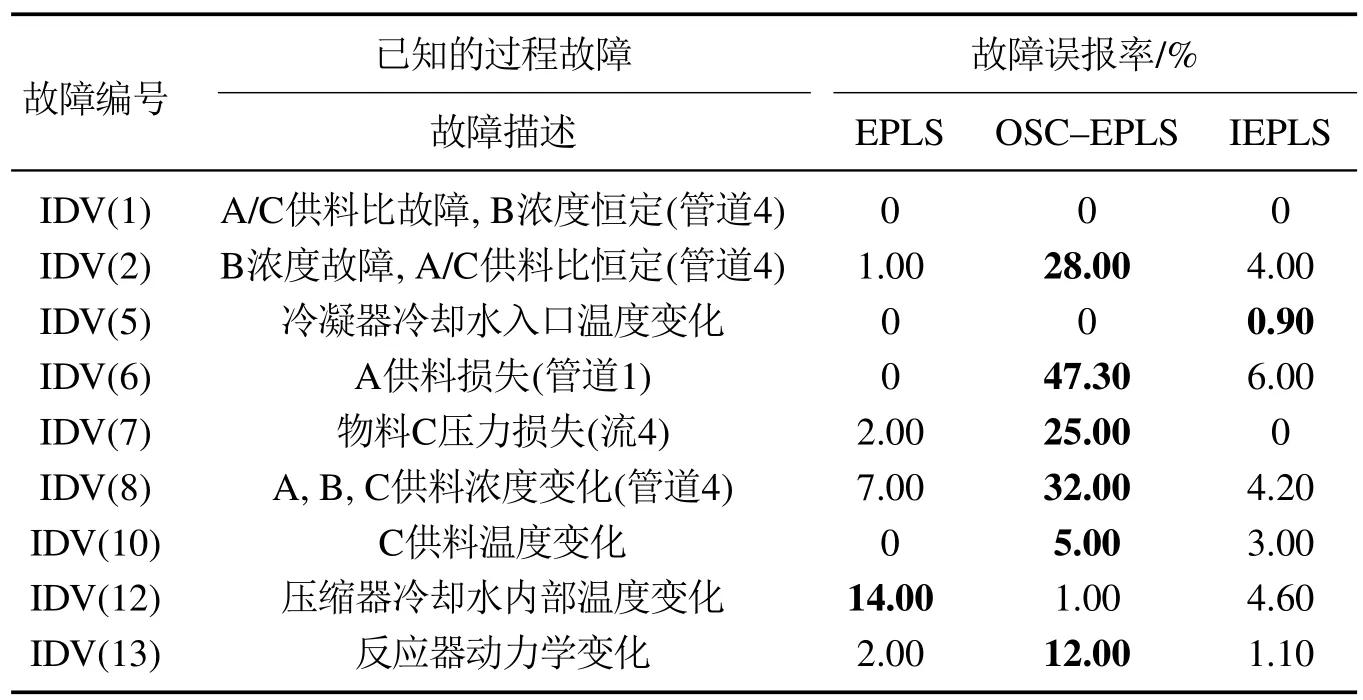
表2 TE过程中3种算法的质量相关故障误报率Table 2 Quality-related fault false alarm rate of three algorithms in TE process

表3中给出了3种算法的质量无关故障误报率，加粗部分为3 种算法中误报率最高的一组.可以看出EPLS算法对质量无关故障的检测性能整体较差，而OSC-EPLS算法的质量无关故障检测性能明显优于EPLS，其中IDV(9)的质量无关故障误报率仅0.87%，可以看出OSC-EPLS算法明显降低了质量无关故障的误报率.本文所提的IEPLS算法除了在IDV(3)，IDV(9)和IDV(11)的误报率高于OSC-EPLS算法0.98%，5.8%和7.34%以外，其余各组的质量无关故障误报率均低于OSC-EPLS.最后，根据多次实验得出的实验数据可以看出本文所提的IEPLS算法在保持质量无关故障误报率较低的情况下，其质量相关故障检测性能明显提高，对于工业过程故障检测而言具有更好的实际应用效果.

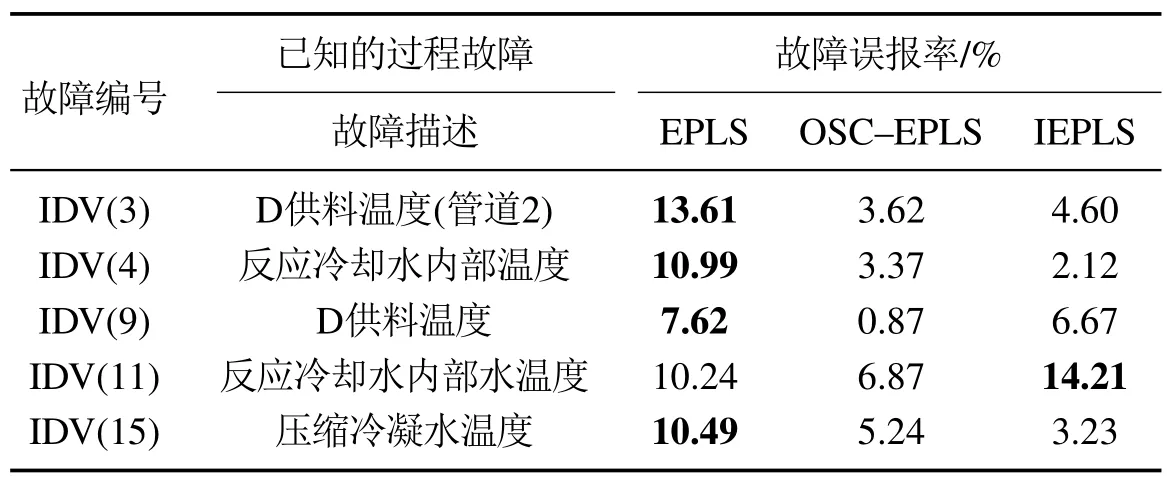
表3 TE过程中3种算法的质量无关故障误报率Table 3 Quality-unrelated fault false alarm rate of three algorithms in TE process

5.3 基于IEPLS的故障诊断方法

在本节中，分别使用基于传统的贡献图方法和基于新息贡献率方法对IDV(8)进行故障诊断.当故障8数据到来后，管道4中出现了ABC供料比变化的随机故障，直接影响的是过程变量4即物料A和C流量，这时由于系统的闭环反馈控制原因，其他的变量如质量变量和操作变量26也受到了该故障的影响.图6所示为使用传统贡献图方法对IDV(8)进行故障诊断的结果，可以看出当故障8数据到来后，传统贡献图的诊断结果表明变量16，18～20，31做出了主要贡献.然而，传统贡献没有诊断出变量4的贡献，这与实际的故障情况并不符合，由此可以看出基于传统的贡献图故障诊断方法并不能够完全准确诊断出故障变量.

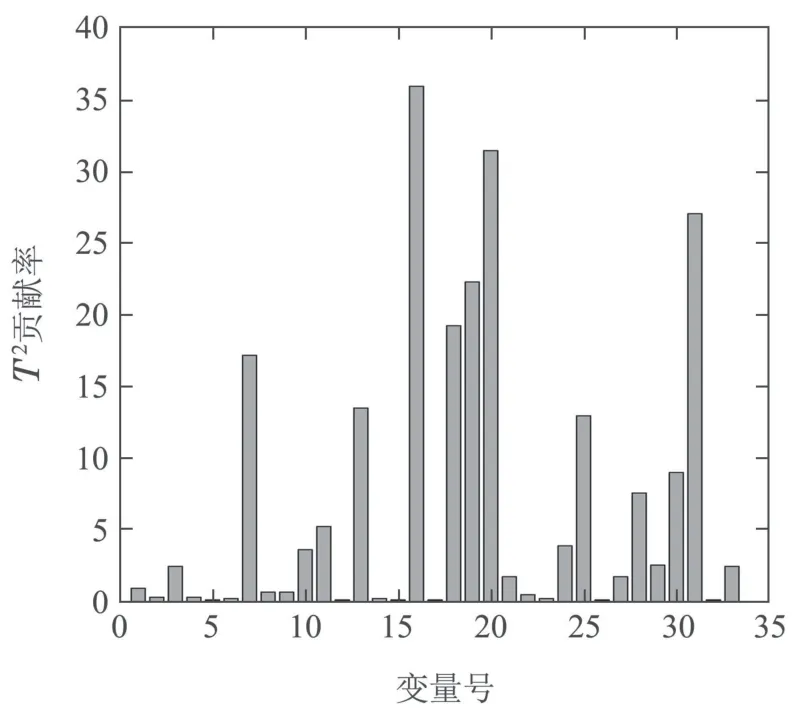
图6 基于贡献图的IDV(8)故障诊断结果Fig.6 The fault diagnosis result of IDV(8)based on contribution plot

图7所示为使用新息贡献率方法对故障8进行故障诊断的结果，从图中可以看出IEPLS对故障8的诊断结果显示出变量4对故障8的主要贡献.另外，IEPLS同时也诊断出了变量8～11，20～22，26～28对故障8的贡献结果，此诊断结果与真实情况是吻合的.实验结果表明，所提的IEPLS故障诊断算法明显优于传统贡献图方法的诊断性能.

图7 基于IEPLS的IDV(8)故障诊断图结果Fig.7 The fault diagnosis result of IDV(8)based on IEPLS

6 结论

本文通过在EPLS的质量相关子空间设计新的统计量和控制限，并将新息贡献率应用在该空间提出了一种基于IEPLS的质量相关故障诊断方法.该方法首先使用正常数据获得模型参数，然后对输入数据进行空间分解.通过在分解后的质量相关子空间设计新的统计量和控制限检测质量相关故障，接着结合新息贡献率对已发生故障的各个变量进行定位，最后得出发生故障的变量信息.通过TEP 仿真平台与EPLS 和OSC-EPLS 的实验结果对比分析，所提IEPLS算法不仅提高了对质量相关故障的检测性能，而且IEPLS对故障变量的定位性能也明显提高.值得一提的是，IEPLS算法的质量无关空间虽然对产品质量的影响可以忽略不计，但是提高其监控性能将是本课题继续研究的一个方向.