非泊松工件流CSPS系统的Q学习算法适用性仿真研究

苏 娜，唐 昊 ，戴 飞，王 彬，周 雷

(1.合肥工业大学电气与自动化工程学院，安徽合肥 230009;2.合肥工业大学计算机与信息学院，安徽合肥 230009)

1 引言

在现代制造领域的一些柔性生产线上，传送带给料加工站(conveyor-serviced production station，CSPS)是一种典型生产单元，具有广泛的代表性.例如，在当前智能制造时代涌现出的越来越多的机器人生产线，在生产线上每个机器人工作站往往可看作是一个CSPS.通常情况下，CSPS系统是通过匀速传送带将待加工工件送至加工站点，加工主体为其提供加工服务.然而在一些实际生产中，可能存在各种不确定因素，例如工件到达可能是随机的，加工站对工件的加工服务时间也可能是随机的，这些不确定性因素会对加工站的生产调度带来困难，从而影响生产率的提高和生产服务水平的提升.因此，对随机不确定CSPS的生产调度优化控制问题进行研究，是当前智能制造时代的一个有意义的研究课题.

CSPS系统的研究可追溯到20世纪八九十年代[1]，其中，日本工业工程领域的松井正之教授以加工站的工件缓存库空余量为状态，以加工主体的前视距离为决策变量，将单站点CSPS 的捡取和加工调度问题转化为前视距离控制问题，并且建立了相应的半马尔可夫决策过程(semi-Markov decision process，SMDP)模型[2].在此基础上，文献[3]结合Q学习思想，提出一种在线策略迭代方法以解决CSPS系统的最优控制问题，而且文献[4]进一步给出了需求驱动CSPS系统的SMDP模型和Q学习优化求解方法.然而，在现有的研究中，工件的到达过程一般都假设为标准泊松过程以保证CSPS系统的前视距离控制可以建模为SMDP，然后通过策略迭代等理论方法或Q学习等仿真方法来获得最优或次优控制策略[4-5].然而在实际生产中，工件的到达可能不严格满足泊松过程这种标准假设[6]，即工件的到达过程不满足Markov性，则CSPS系统无法建立为SMDP模型.但是，支撑Q学习算法的数学基础是MDP模型或更为一般的SMDP模型[7]，而当系统决策优化问题无法建立成此类模型时，一般难以在理论上证明Q学习优化算法的最优性或收敛性.

当前，Q学习或深度Q学习类的学习优化算法已被大量用于非严格Markov过程或半Markov过程所能描述的一些系统的决策优化问题，并且也取得了较好的学习优化效果[8-10].因此针对非泊松工件流CSPS系统，Q学习算法是否依然可以学到较好的控制策略是值得分析讨论及仿真验证的问题.

在非标准泊松过程中，马尔可夫调制泊松过程(Markov modulation Poisson process，MMPP)是一个极具代表性的随机过程[11-13]，常被国内外学者用于描述计算机、通信、金融和股市等业务流的随机统计分布模型.例如，文献[12]采用高速MMPP 过程到达的渐近分析方法，对无限服务器排队系统中访问信息的总容量进行分析;文献[13]基于MMPP构建了一个交易量分离模型，将交易量中的异常交易量分离，解决了交易数据受异常事件污染的问题.半马尔可夫调制泊松过程(semi-Markovian modulation Poisson process，SMMPP)是较MMPP更为广泛的一类随机过程，其到达率参数变化的时间间隔可扩展为非指数分布的一般分布[14-15].例如文献[16]对ACPGRP计数过程进行扩展，将其中的基础更新过程用SMMPP代替，并建立了一个统一的多变量计数过程.

在上述文献研究的基础上，本文考虑以MMPP和SMMPP到达作为非泊松到达的典型代表，通过仿真方法研究当工件非泊松到达，CSPS 无法被建立为SMDP模型时，Q学习算法的适用性问题.首先在相同的平均到达率下，仿真评估标准泊松与非标准泊松两种情况下的系统性能值，以检验非泊松到达情况下Q学习算法的性能.其次在工件非泊松到达时，每隔一段时间统计工件的平均到达率作为标准泊松到达率，理论求解不同到达时刻的最优策略和理论代价，并将此最优策略作用于原非泊松到达情况下的系统，仿真统计对应的系统代价，作为最优策略评估代价，分析对比最优策略评估代价曲线、理论代价曲线和原非泊松到达Q学习曲线，以检验非泊松到达情况下Q学习的优化效果.最后讨论当工件以MMPP和SMMPP混流到达时Q学习的适用性问题.

2 CSPS系统

CSPS系统的物理模型如图1所示[3]，由传送带、机器人(agent)、缓存库、成品库组成.其中工件随机到达，通过匀速运动的传送带输送至加工站点.缓存库的容量有限，用来存放从传送带上卸载的待加工工件，成品库用来存放加工好的工件.前视距离为从固定捡取点往传送带上游观测的一段距离，根据决策时刻的系统状态和控制策略动态变化.

图1 CSPS系统的物理模型Fig.1 Physical model of CSPS system

假设缓存库容量为Z，定义缓存库的空余量为系统状态S，其状态空间Φ={0，1，···，Z}，定义vs为系统在状态S的行动，即前视距离.在决策时刻，agent根据系统当前状态S选取一个前视距离vs.由于待加工工件沿传送带随机达到，则前视距离内有可能有工件，也有可能无工件.若为前者，则agent采取捡取动作，即等待第1个工件到达捡取点并卸载至缓存库;若为后者，则agent采取加工动作，即从缓存库中取出一个工件进行加工，同时在此定义系统的一个平稳策略为v.

在MMPP 或SMMPP 型非泊松工件流CSPS 系统中，工件的到达率状态会按一个Markov 过程和半Markov过程进行迁移.记当前及下一到达率状态分别为m和m′.记Tn为第n个决策时刻，在每个决策时刻，先观测缓存库的状态，若缓存库为空，agent只能采取捡取动作;若缓存库为满，agent只能采取加工动作;若缓存库非空亦非满时，则根据前视距离内是否有工件来决定采取相应的动作，若采取的是等待捡取动作，则捡取完成后即进入下一决策时刻，若采取加工动作，则经过max(vs，τ)时间后系统进入下一决策时刻，其中τ是实际加工时间.加工服务过程可能是确定的，也可能是随机的，为保证一般性，一般假设加工服务时间服从Erlang分布.此外，在加工过程中，若仍有工件到达，则流失[3].非泊松工件流CSPS系统决策时序关系如图2所示，其中，第n个和第n+2个决策周期分别对应加工动作(后者存在无后效性处理，即需要等待延迟时间ω后，进入下一决策时刻)，第n+1个决策周期对应捡取动作.

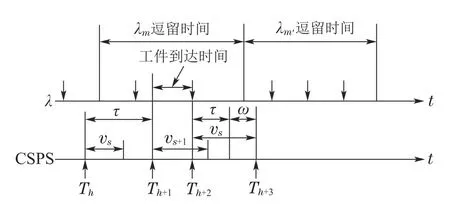
图2 非泊松工件流与CSPS系统时序图Fig.2 Non-Poisson parts flow and time sequence of CSPS system

3 MMPP和SMMPP模型及优化方法

MMPP本质上是一个非平稳泊松过程，其中瞬时泊松到达率服从一个平稳的随机过程.MMPP一般用于描述一类被Markov过程所调制的泊松到达过程，并同时用于描述时变到达率和到达间隔之间的相关性[17].与工件到达率固定不变的标准泊松流相比，MMPP工件到达是指工件达到率的变化序列按照Markov链进行转移，每个达到率参数状态的持续时间服从指数分布[18].换言之，MMPP是到达率受某个连续时间Markov过程控制的随机过程，即到达率参数随此随机过程状态的转移而变化.而SMMPP是较MMPP更为广泛的一类随机过程，描述的是到达率受半Markov过程控制的泊松过程，其到达率参数状态的持续时间服从一般分布.

3.1 MMPP模型

当工件以MMPP到达时，到达率参数受Markov链调制，即到达率参数状态的转移按Markov过程变化，记MMPP的状态空间为ΦMP={1，2，···，N}，到达率参数为λn，n ∈ΦMP，令到达率由状态i转移到状态j的概率为Pij，则其状态转移矩阵为

另外，假设到达率参数的状态逗留时间函数服从参数为θ(λn)的指数分布:

则到达率参数变量在状态n的转移率Λn=θ(λn).记该连续时间Markov链的无穷小矩阵为

该连续时间Markov过程的稳态分布π=(π1，π2，···，πN)可由平衡方程πe=1，Ae=0，πA=0所唯一确定[19-21].其平均到达率由其稳态分布确定[11]:

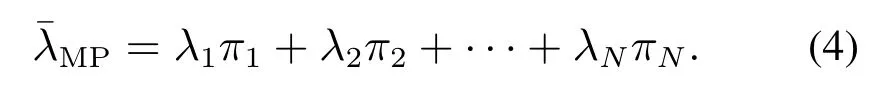
3.2 SMMPP模型

工件以SMMPP到达时，其到达率参数状态转移过程服从半Markov过程，SMMPP是较MMPP更为广泛的一种随机过程，是MMPP的推广，不同的是SMMPP的到达率参数状态的逗留时间未必服从指数分布，可以是一般分布.记SMMPP的状态空间ΦSM={1，2，···，M}，到达率参数为λm，m ∈ΦSM，其状态转移矩阵为

在工件流按SMMPP变化时，若到达率由状态i转移到状态j，且到达率状态在状态i的逗留时间服从任一随机分布Fij(t)，则对应此转移的状态i的平均逗留时间为

因而，状态i的平均逗留时间满足[19]

另外，到达率参数状态变化过程的嵌入Markov链的稳态分布δ=(δ1，δ2，···，δM)满足[19]

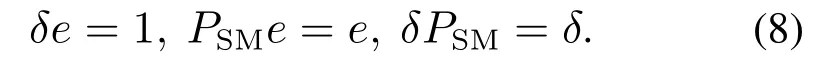
于是对应此SMMPP的稳态分布Π可以由下式求出[22]:

工件的平均到达率唯一确定，可由下式求出[11]:

3.3 CSPS系统优化方法

一个典型的生产周期包括等待时间和加工时间，而加工时间服从固定的随机分布，因此通过合理的生产调度降低等待时间可以有效的降低系统生产周期，从而提高系统生产率.因此在非泊松工件流CSPS 系统中，主要考虑等待时间代价，并设置单位时间等待代价系数为k.假设当缓存库状态为Xt时，agent采取行动vXt，随机逗留一段时间后系统状态转移到下一个状态Yt.此转移过程中，记单位时间代价函数记为f(Xt，vXt，Yt)[3]，在策略v下系统无穷时段平均代价为

工件非标准泊松到达时，分别给定MMPP和SMMPP的到达率参数状态空间、状态逗留时间分布函数和状态转移矩阵，即可产生MMPP和SMMPP到达的工件流序列.由于工件的到达率动态变化，难以将CSPS系统建立成SMDP模型，因此借鉴文献[5]中基于模拟退火的Q学习算法来学习系统的控制策略.在离线仿真中，在每一决策时刻，需实时调用当前工件流序列以判断前视距离内是否有工件.在实时在线学习中，根据生产线上的工件序列位置信息即可判断前视距离内是否有工件.Q学习算法中，先初始化Q值表，设置初始温度T、Boltzmann常数K和温度衰减因子ξ.在学习过程中系统从探索行动和贪婪行动中随机选择，并不断更新Q值表，温度T每学习R步后根据衰减因子ξ降低，当满足算法终止条件时结束学习，学到最终策略，并仿真统计系统代价.

为了评估上述Q 学习算法的学习效果，在仿真实验中，定义一个标准泊松流CSPS系统，其工件到达率与MMPP或SMMPP的平均到达率一致.此时，工件到达的间隔时间分布为t ＞0.当工件以该标准泊松过程到达时，CSPS 系统可建立成SMDP模型，一方面可以利用前述基于模拟退火的Q学习算法来学习系统的最优或次优控制策略;另一方面，根据参考文献[3-4]，可通过定义等价无穷小矩阵和等价性能矩阵将该SMDP模型转化成等价的连续时间Markov决策过程，然后通过策略迭代算法求解出系统的最优策略，并得到系统的理论最优代价[19-21].然后，将该最优策略作用于原非泊松流CSPS系统，通过仿真统计该策略作用下的系统运行效果，从而与直接针对原非泊松流CSPS系统的Q学习算法效果进行比较验证.并且也可分析比较两种非泊松流CSPS下的Q学习算法与对应的标准泊松流CSPS系统下的Q学习算法的学习性能.

4 仿真实验结果

在本文的仿真实验中，工件的加工时间服从L阶的Erlang分布[5]，每相的加工时间服从参数为µ的指数分布.这里设置µ=4，L=4，加工一个工件需要平均耗费时间=1.由于不同工件流CSPS系统的工件到达随机规律不一样，但在仿真实验中，为了保证不同工件流在长时间尺度内单位时间内平均到达工件个数统计意义上相等，同时为了遵循“一进一出”的产线基本平衡原则，均选取理论平均到达率=1.在到达率和服务率都固定为1时，最优平均代价理论上会随着缓存库容量的增大而降低，但在缓存库容量设置为5时，平均代价的下降就已接近饱和[2]，所以仿真实验中，将缓存库的容量Z设置为5.设置前视距离最大范围lmax=1，前视距离的离散度Δ=0.1.系统相关参数设置如表1所示.

表1 系统相关参数设置Table 1 The parameter setting of system

为了便于对比，无论工件是按MMPP 到达还是以SMMPP到达，都假设到达率状态总数为M=N=4且状态空间相等.其中:λ1=0.85，λ2=0.95，λ3=1.05，λ4=1.15.此外，到达率参数状态的转移矩阵皆为

当工件以MMPP到达时，状态逗留函数F(t)的参数选取θ(λ1)=0.04，θ(λ2)=0.02，θ(λ3)=0.02，θ(λ4)=0.04.根据式(1)-(4)计算出MMPP的平均到达率=1，状态平均逗留时间HM=(25，50，50，25).

当工件以SMMPP到达时，状态逗留函数Fij(t)服从一般分布，本文主要考虑均匀分布.令Fij(a(λm)，b(λm)，t)为服从区间[a(λm)，b(λm)]之间均匀分布，表达式如下:

参数选取如表2 所示，根据式(5)-(11)和式(13)可计算出平均到达率=1，状态平均逗留时间HSM=(20，25，25，20).

本课题组经过多方商榷与实践，探讨得出地方师范院校数学本科专业基于核心素养下的课堂教学设计模板，并以“反常积分的概念”作为教学课题展开课堂教学设计，将数学核心素养的培育融入大学数学课堂，积极投身高等数学课堂教学改革。课堂教学案例如下：

表2 SMMPP相关参数Table 2 Related parameter of SMMPP

在工件按SMMPP到达的情况下，Q学习算法学到较好的控制策略为vSM=[0 0.4 0.5 0.7 1 inf].而在标准泊松到达情况下，Q学习学到最优或次优控制策略v=[0 0.3 0.6 0.8 0.9 inf]，在以上策略中，inf表示无穷大.工件分别以MMPP和SMMPP到达的Q学习优化曲线如图3(a)和3(b)所示.工件以标准泊松到达的Q学习优化曲线如图3(c)所示.图3(d)给出非泊松到达情况下Q学习学到的策略与标准泊松到达情况下Q学习学到的控制策略的对比图.

当工件非泊松到达时，到达过程不满足Markov性且更为复杂，因此Q学习在决策时选择前视距离也更为复杂.已有研究结果表明标准泊松到达情况下，Q学习能学到较好的控制策略，从图3(a)-3(c)可以看出，几种情况下Q学习统计的系统代价结果很接近，在学习步数达到800步以后系统代价均保持在较小的范围内，最终系统代价都保持在0.65附近.综上说明非泊松到达Q学习依然可以学到较好的控制策略，并且以该策略评估的系统代价与在标准泊松到达情况下，以平均到达率作为工件到达率的Q学习结果非常接近.从图3(d)可以看出当缓存库空余容量越大，前视距离越大，所以系统会更倾向于捡取工件而不是加工工件;当缓存库容量越小，前视距离越小，所以系统会更倾向于加工工件而不是捡取工件，这也符合实际生产情况.

图3 Q学习结果，=1Fig.3 Q-learning results when average arrival rate equals to 1

系统优化的目标是找到最优控制策略使得在平均折扣准则下，长远期望代价最低.然而在实际的生产过程中，系统的生产率、生产效率、生产周期这些系统性能指标，可以更好地作为评价系统是否可靠的标准.在相同的工件到达率和系统工件加工率情况下，系统的生产率、生产效率越高，生产周期越低说明在同等的时间下系统的产量越高、加工的工件越多.系统的生产率、生产效率、生产周期可通过理论计算和蒙特卡洛仿真统计求出[5].

理论计算方法中，一个生产周期Y 由等待时间和服务时间组成.系统期望生产率PR为期望平均时间的Y 倒数，期望生产效率PE为期望平均时间Y 与工件到达率λ乘积的倒数.采用蒙特卡洛仿真统计方法也可以统计系统生产率PR和系统生产效率PE，系统生产率PR即[0，T]时间段内平均加工工件的个数，[0，T]时间段内加工工件个数占总到达工件个数的百分比即系统生产效率.

下面分别在非标准泊松到达和标准泊松到达两种情况下，分析讨论系统性能值的差异.分别选取vMP，vSM作用于原非泊松系统，选取v作用标准泊松系统，做10次独立实验，每次独立实验系统仿真运行5000步，然后取相关性能值的统计平均值.另外，给出标准泊松到达情况下策略迭代算法理论求解的系统性能值作为非标准泊松到达情况的对比.各种情况下系统性能值的结果如表3所示.

表3为不同评估方式下系统性能值的比较结果，由表可知在非标准泊松到达与标准泊松到达情况下，Q学习的结果和理论求解的结果都非常接近，说明在工件非泊松到达情况下，Q学习依然可以学到较好的策略，并且以该策略评估的系统性能值与在标准泊松到达情况下，以平均到达率作为工件到达率的Q学习结果非常接近.

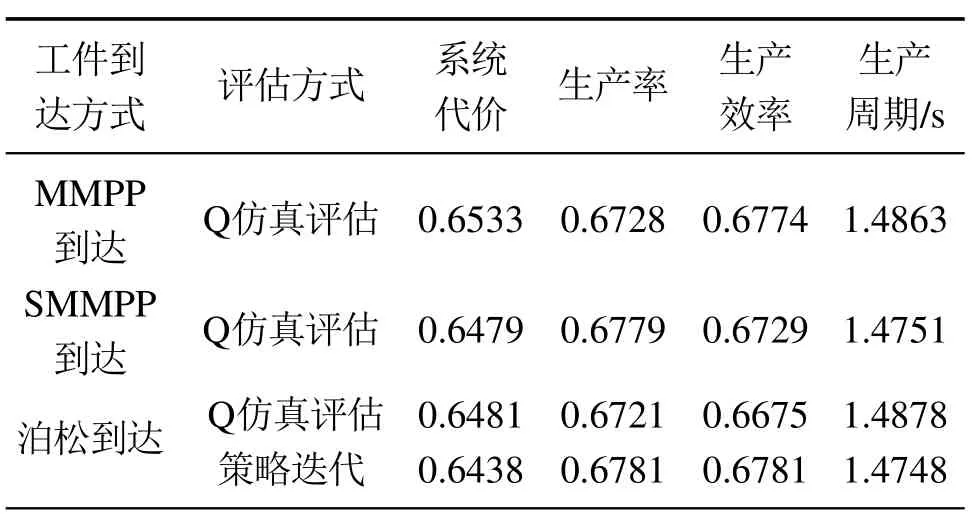
表3 不同评估方式下系统性能值Table 3 The performances under different evaluation methods

另外，本文分别在MMPP工件到达和SMMPP工件到达情况下进行10次独立样本轨道的学习，每800步记录一次各样本轨道平均代价，并分析其平均值和标准差，以此来研究在MMPP工件到达和SMMPP工件到达情况下Q学习算法应用在CSPS系统时的稳定性，如图4所示.曲线为每一个所记录的平均代价的平均值，填充区间为这10条样本轨道所得数据在各点处的标准差区间.其意义在于，若假设这些样本数据满足高斯分布，那么相信这些所得样本的均值有68%的概率落在此标准差区间内.而填充区域面积越小，则表明不同样本轨道得出的结果越接近.由图4可知，在算法后期，不同样本轨道得出的数据波动并不大.综上所述，Q学习算法学到的控制策略可以使工件按MMPP到达和SMMPP到达时CSPS系统稳定运行.

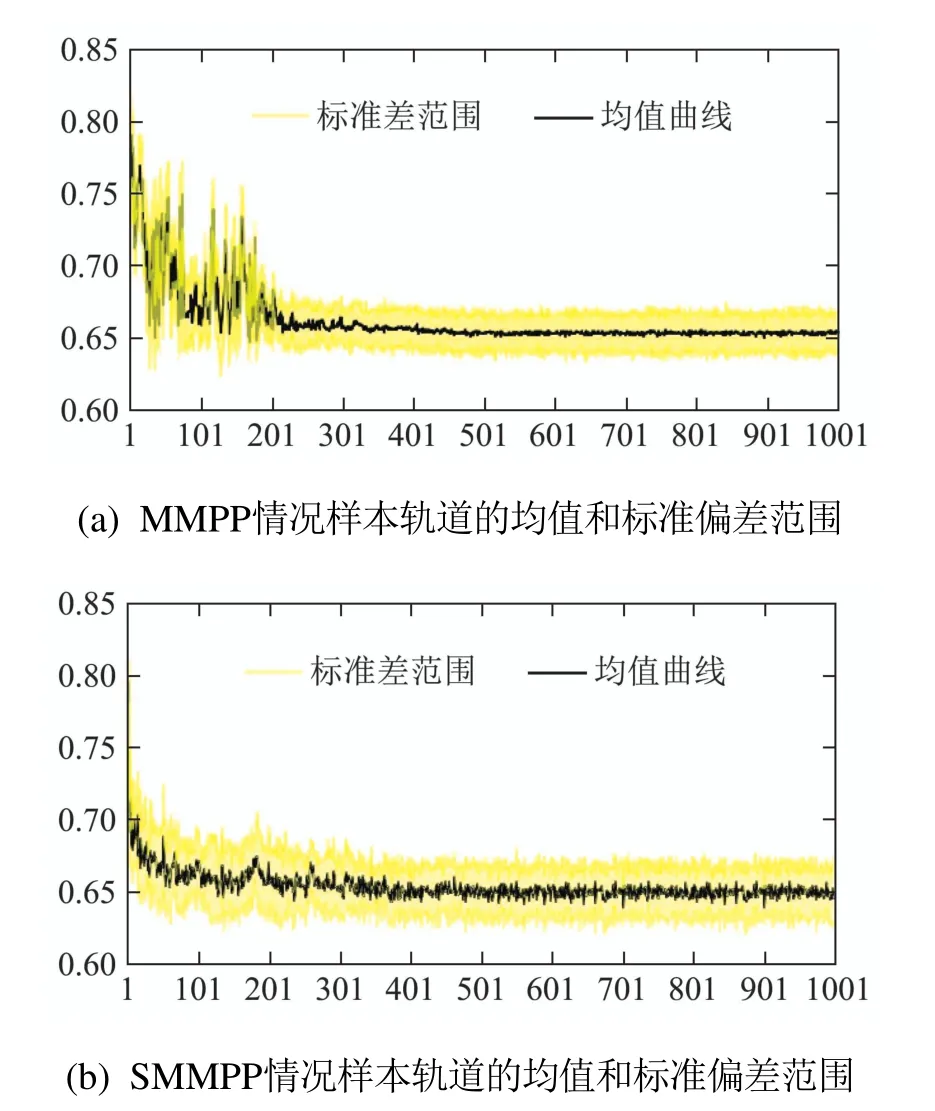
图4 工件非泊松到达情况下10条样轨道的均值和标准差范围Fig.4 Means and standard deviation ranges for 10 sample paths under non-Poisson arrival

图5 Q学习结果，=1.2Fig.5 Q-learning results when average arrival rate equals to 1.2

工件按两种非泊松到达情况下，Q学习算法学到的控制策略分别为

而在工件标准泊松到达情况下，Q学习算法学到的最优或次优控制策略v=[0 0.5 0.6 0.8 1 inf].图6(a)-6(c)分别是平均到达率=0.8时工件以MMPP和SMMPP和标准泊松到达的Q学习优化曲线.图6(d)给出=0.8时非泊松到达情况下Q学习学到较好策略与标准泊松到达情况下Q学习学到最优或次优策略的对比图.

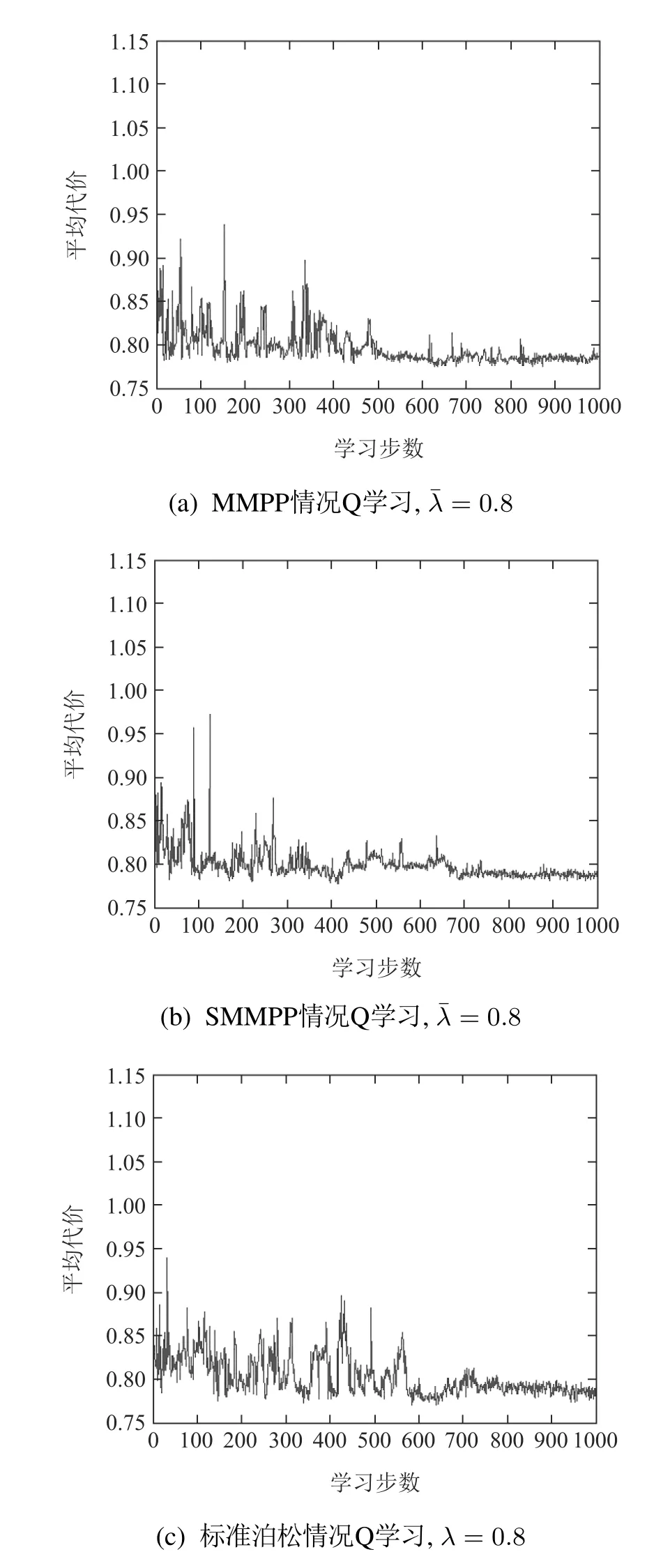
图6 Q学习结果，=0.8Fig.6 Q-learning results when average arrival rate equals to 0.8

本文考虑到即使工件以非泊松流到达，仍然可以统计工件的平均到达率，下面在工件非泊松到达时，观测统计平均到达率的理论学习情况.首先采用蒙特卡洛仿真统计方法，分别对MMPP和SMMPP到达的工件统计平均到达率，定义[0，t]时间段内工件到达个数H(t)，统计平均到达率如下:

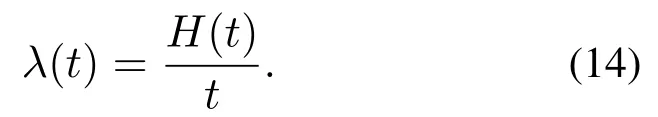
当时间t →∞时，理论上λ(t)会趋于平稳并且近似等于平均到达率分别在工件以MMPP和SMMPP到达，平均到达率=1时，选取与原系统相同的工件到达的样本，每隔一段时间统计λ(t)，由于Q学习的步数达到100步左右时，工件的λ(t)已经趋于平稳，因此前100 步内每隔10 步统计一次λ(t)，100步后每隔100步统计一次λ(t)，统计结果如表4所示.从表4也可以看出随着到达的工件越来越多，统计的λ(t)越来越接近于平均到达率统计不同到达时刻的λ(t)作为工件标准泊松到达率，建立SMDP模型后通过策略迭代算法求解λ(t)的最优策略v(λ(t))*和理论系统代价并绘制其理论代价的变化曲线.将此最优策略v(λ(t))*作用于原非泊松到达情况下的系统，做10次独立实验，每次独立实验系统仿真运行5000步，取系统代价的统计平均值，得到λ(t)的最优策略评估代价，并绘制其变化曲线.

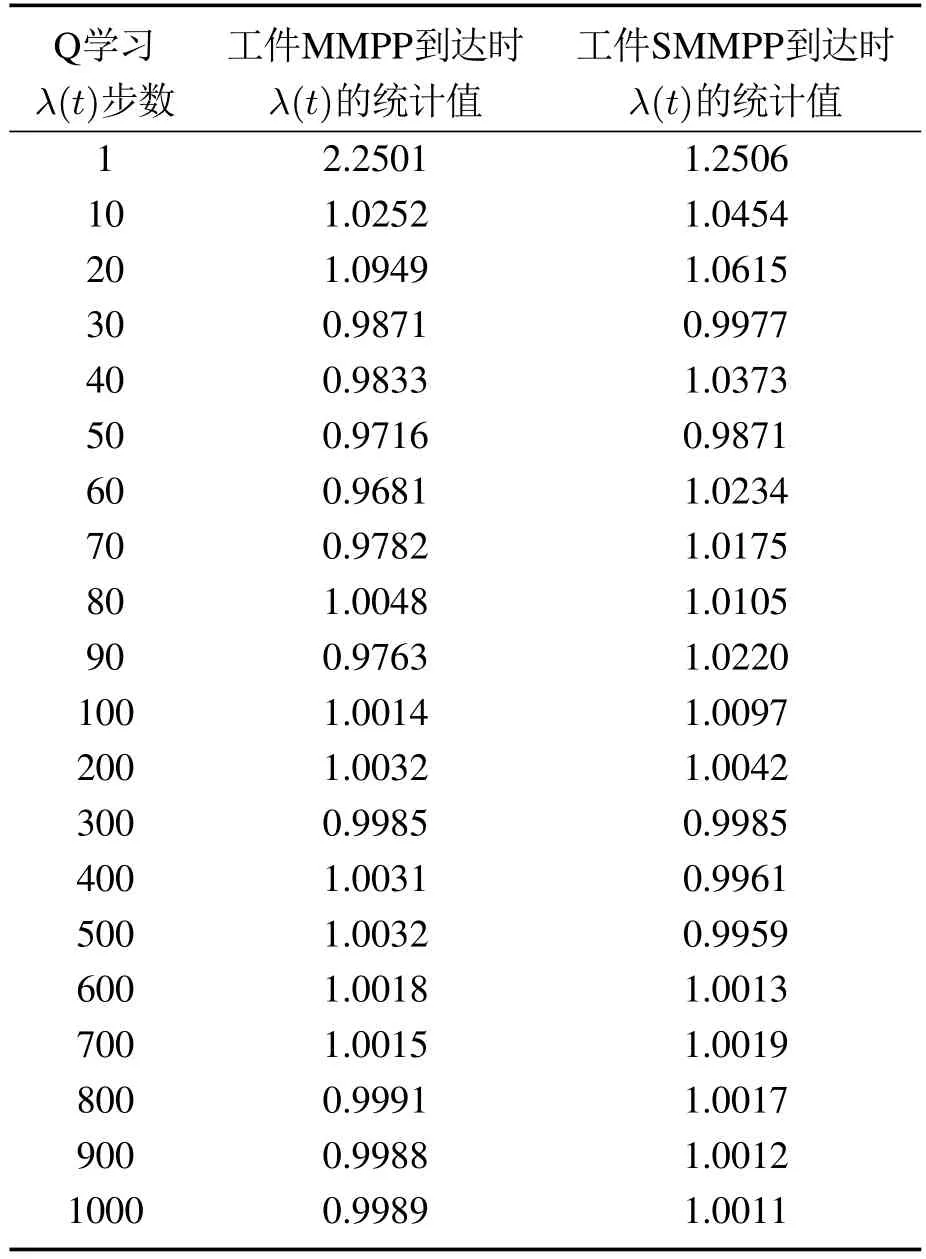
表4 非泊松到达情况下工件λ(t)统计结果Table 4 Statistical results of average arrive rate under non-Poisson distribution arrival

图7分别给出工件以MMPP和SMMPP到达的最优λ(t)策略评估代价曲线、λ(t)理论代价曲线和原非标准泊松到达Q学习曲线的比较图.

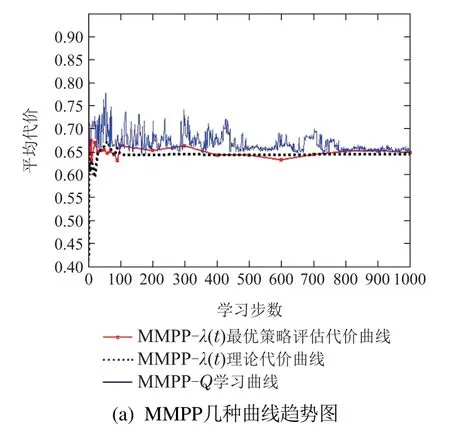
图7 工件非泊松到达的几种曲线趋势图Fig.7 The cost trends under non-Poisson arrival

从图7可以看出在学习步数前100步部分，系统理论代价和最优策略评估代价波动较大，随着工件到达个数的增加，λ(t)趋于稳定，系统理论代价和最优策略评估代价波动趋于平缓，最终近似收敛并与Q学习结果非常接近.理论代价和最优策略评估代价收敛的过程作为λ(t)的理论学习过程，其最终收敛结果与原工件非泊松到达的Q学习结果非常接近，说明非泊松到达情况下的Q学习能学到较好的控制策略，并且在工件非泊松到达时，当足够的工件到达后，以统计平均到达率作为工件标准泊松到达率，理论求解快速找到的控制策略也可作为较好的控制策略.

现讨论工件按SMMPP和MMPP叠加混合到达时，CSPS系统的Q学习算法的适用性问题.在此叠加混合非泊松工件流CSPS系统中，工件以混合信号流形式随机到达，工件的到达过程依然不满足Markov性.仿真中，取M=N=2，且SMMPP的到达率参数状态为λ1=0.45，λ2=0.55，到达率状态逗留时间转移服从均匀分布;MMPP的到达率参数状态为λ3=0.35，λ4=0.65，到达率状态逗留时间服从指数分布.显然，可以推导此混合工件流的理论平均到达率=1.图8是按此混流信号产生的非泊松工件流序列的示意图.

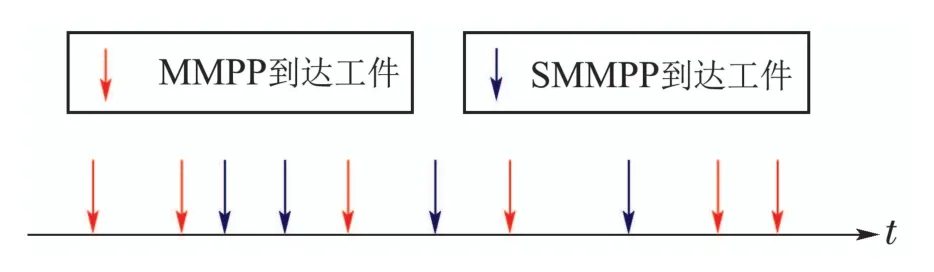
图8 叠加混合非泊松工件流Fig.8 Mixed non-Poisson parts flow

叠加混合非泊松工件流CSPS系统Q学习优化曲线如图9所示.由图可知，刚开始Q学习曲线波动较大，随着学习步数增多，曲线趋于平缓，最终系统代价保持在0.65附近，此结果与工件标准泊松到达情况下=1时的Q学习结果非常近似，此时学到的控制策略为v=[0 0.5 0.6 0.7 1 inf]，满足v0＜v1＜···＜v5，符合现实情况.说明即使工件以叠加混合非泊松信号流随机到达时，Q学习也能学到较好的控制策略.

图9 叠加混合非泊松工件流Q学习Fig 9 Q-learning of mixed non-Poisson parts flow

另外在叠加混合非泊松工件流CSPS系统中，Q学习评估的各类系统性能值如图10所示，从图中可以看出，当工件以叠加混合非泊松流到达时Q学习评估的系统性能值与标准泊松到达情况下Q学习评估的系统性能值非常接近.

图10 叠加混合非泊松工件流下系统性能值Fig.10 System performance value under and mixed non-Poisson parts flow

5 结论

本文通过对比标准泊松与非标准泊松的Q学习结果，验证了在工件到达过程不满足Markov性，CSPS无法建立为SMDP模型的情况下，Q学习算法依然可以学到较好的控制策略.以该策略评估的系统代价与在标准泊松到达情况下，以平均到达率作为工件到达率的Q学习结果非常近似.另外在工件非泊松到达时，当足够的工件到达后，以统计工件的平均到达率作为标准泊松到达率，理论求解快速找到的控制策略也可作为较好的控制策略，并且以此控制策略作用于原非泊松到达情况下的系统，评估的系统代价与Q学习统计的系统代价非常接近.另外，验证了工件以叠加混合非泊松流随机到达时，Q学习也能学到较好的控制策略.