向结论更深处追寻数学的深度——《3的倍数的特征》教学

李翠红 姚俊俊

【课前思考】

人教版《3 的倍数的特征》的编排注重学法指导，通过小组合作在《百数表》中观察、发现形成猜想，并进一步验证猜想，由此形成结论：3 的倍数各个数位上数的和是3 的倍数，并把研究的数从《百数表》中3 的倍数扩展到“任意几个3 的倍数”等。但是否绝大多数学生都能通过观察形成这样的猜想？还是直接根据同伴的结论来进行验证？结论背后所承载的算理都理解了吗？于是，笔者有了以下慎思。

慎思之一： 如何确定学习起点和学习难点。

《3 的倍数的特征》教学是顺着学生研究2、5 的倍数的特征的经验，引导学生在《百数表》上进行研究。通过观察学生自主探究活动的情况发现，由于先前学习2、5 的倍数的特征主要看个位，因此学生很自然地希望通过观察个位的规律来判断一个数是否为3 的倍数，但发现在《百数表》上横着看3 的倍数的个位上的数可以是任意数。原先的方法行不通了，那么应该怎么引导学生发现3 的倍数的特征呢？找到了学生的学习起点，也就找到了解决问题的钥匙。如何突破难点，将学生的观察引导到各个数位的数字上来，教师可以借助计数器，让学生来拨数，教师通过听计数器珠子落下的声音次数来判断是否是3 的倍数，将问题的关键引导到观察各个数位的数字上去，再通过同伴间的讨论，得到猜想：3 的倍数是否与各个数位上数的和有关。

慎思之二： 如何引导学生深度学习，理解结论背后的算理。

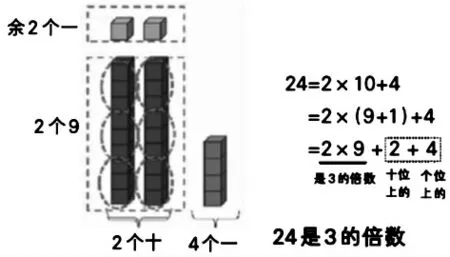
学生验证了“3 的倍数的特征”这一结论后，运用特征来进行数学知识应用，用卡片组数、快速判断等环节就是运用所学知识把结论进行验证和应用。而学生是否知其然更知其所以然呢？教师要让学生在理解的基础上进行深度学习，开展深层次的思考，教师进一步启发学生思考：“3 的倍数为什么会有这样的特征呢？”问题是学生好奇心的表现，也是激发学生学习的原动力。课堂以探究问题为抓手，以问题来驱动引导学生深度学习。以数字24 为例，从各个数位的数字之和的角度思考，为什么是3 的倍数？可以组织学生通过小组合作探究，通过拆数：24=2×10+4，24=2×9+2+4，2×9必定是3 的倍数，那么2+4 恰好是各数位的数字之和，如果是3的倍数，整个数也就是3 的倍数了。于是，学生也就从本质上理解了3 的倍数的特征了。

慎思之三： 如何完善知识结构，沟通新旧知识联系。

掌握了“3 的倍数的特征”后，学生发现此特征与先前学习的“2、5 的倍数的特征”初看不具有统一性，思考角度不同，一个通过个位数字来判断，而另一个通过观察各数位数字之和来判断。但再进行深层次探究，引导学生尝试用同样的思路来研究2、5 的倍数的特征，学生也能悟出类似的道理：百位、十位上的几百、几十一定是2、5 的倍数，如果个位上的数也是2、5 的倍数，这个数就是2、5 的倍数，所以2、5 的倍数的特征只看个位就可以了。这样把2、5 的倍数的特征与3 的倍数的特征从本质上统一起来。尽管特征的表述看似完全不同，但其判断的准则是一致的，从而在更深层次上引领学生进行知识建构，将新知纳入原有的认知结构中，形成新旧知识间的沟通与联系。

【教学过程】

一、激趣导入

竞猜活动：学生随便说一个数，教师判断是不是3 的倍数。

二、自主学习

师：请你写出100 以内3 的倍数，写完后观察这些数，你有什么发现？同桌相互说一说。

三、合作探究

师：我们知道，判断一个数能否被2、5 整除，只看它个位上的数就可以了。那么，判断一个数能否被3 整除，是不是像2 和5 一样也只看个位就行了呢？我们不妨试试看。

师：请每位同学找两个被3整除的数，观察这些数的个位，你发现了什么？（指名汇报）

生：没有规律。

电子商务的概念最早来源于美国，主要是将线下商务机会与互联网相互结合，让互联网成为线下交易平台，这是一种全新的商业模式。也是对传统经营模式的一种考验与挑战，同时也需要依靠传统模式为基础进行支撑。在消费者的心理，连锁企业统一的品牌、良好的形象以及规范的服务早就已经深入人心。但是很多连锁企业却安于现状，没有紧跟时代发展的步伐进行不断的完善与创新，通过整合自身资源在互联网的辅助下增强自身实力。因此，连锁企业的经营管理创新需要互联网的帮助，才能实现经营模式的全面创新。

师：从这些数中，我们可以看出，3 的倍数的个位上可以是任何数，我们无法确定个位上是几，是吗？所以，光凭看个位的“经验”是行不通的，那3 的倍数到底有没有特征呢？现在我们再来试一试。这样，我们交换一下角色，你来问我来答，好吗？请中间一大组的同学在计数器上随便拨一个多位数，要求一颗一颗地拨，看我能否准确而迅速地判断该数能不能被3 整除，其余的同学当评委来算一算，判断我说得对不对。（师生互动）

师：我刚才之所以能准确而迅速地判断出一个数是3 的倍数，是因为3 的倍数具有一定的特征，这个特征到底是什么呢？有关结论的获得，我为你们提供了两条途径，请选择：1.由我直接告诉你；2.由你和你的小组成员在操作中探索获取。

师：好！老师就为你们的探索引条路，请看屏幕：（课件出示）

请各小组拿出数字卡片，用卡片按一定顺序组数，使组成的数不重复、不遗漏。试算一下，组成的这些数都能不能被3 整除？

每组两位同学用卡片摆数，一位做记录，一位负责用计算器计算，看看你们会有什么发现？

（教师根据学生的汇报适时板书）

师：同学们先看前两组数，回想一下，我们在用卡片组数时什么发生了变化？也就是无论数位怎么变化，都不影响它是否为3的倍数，是不是？由此可见，是否为3 的倍数与这个数的“数位”有没有关系？那与什么有关呢？对！与组成这个数的几个数字有关，到底与数字的什么有关呢？

师：请大家认真看黑板上的这三组数，边观察边思考，大胆猜想，有一定的想法后与小组成员交流一下，看哪一组能得到最有价值的猜想。

师：先独立思考后小组讨论，再进行汇报交流。

师：刚才这只是我们的猜想，它是否完善还需要我们进一步地去验证，现在请各学习小组按要求验证：听好分工，一位同学任意说一个多位数，一位同学计算，一位同学判断，一位同学做好记录，看看同学们的猜想能否得到验证。

师：得到验证了吗？说明我们的猜想是正确的！能被3 整除的数为什么有这样的特征呢？请同学们举例来说明。

四、巩固练习

1.完成教材第10 页的“做一做”。

2.要使下面的数是3 的倍数，□中有几种填法？

□7 4□2

3.按要求填数。

（1）56□，使其成为2、3 的倍数。

（2）117□，使其同时是2、3、5 的倍数。

（学生独立完成，鼓励学生不但会做，还要善于发现方法）

4.请同学们每人写出5 个能被3 整除的数，写完后交给同桌，相互判断，并纠错。

五、全课总结（略）

【课后反思】

一节课结束了，但研究还远远没有结束，课后我给学生布置了课堂作业：

1.为什么2 和5 的倍数只看个位上的数就可以了？

2.寻找9 的倍数的特征。把你的想法写一写，画一画。

学生有了课堂上的研究经验，有了对知识的透彻理解，才能举一反三，研究出更多的背后的算理，把知识学得通透、明白。下课了，学生感叹：“本来以为学习数的知识会很枯燥，没想到这么有意思，我喜欢这样的数学课。”我顿时觉得这就应该是数学课本来该有的样子吧！

数学是一门高度抽象的学科，如果一节课仅仅停留在知识层面：知道3 的倍数的特征并会进行判断，学生的分析、判断、推理能力就得不到有效提升。应该让学生在教师用心设置的教学情境中悟出数学之趣，产生一探究竟的迫切愿望，主动地投入深度学习之中。如果忽视学生的学习起点和难点，学生心中的疑惑得不到有效的解答，课堂中学生就会在难点中迷失方向，失去思考的动力，变得没有信心，不爱思考。在数学教学中还有许多的规律、公式，如果教师也都因为其“规定性”觉得没有什么可讲，就直接把结论告诉学生了，显然从促进学生持续发展的角度来看，这样的教学远远不够。如果教师能带领学生在教学过程中清晰地感受到结论背后的原因，看清了背后的本质，这样的过程应该带给学生的不只是知识上的收获，更重要的是让他们真切地感受到数学是有温度的，而不是一串串冷冰冰的数字和公式。探寻3 的倍数的特征背后的奥秘，弄清为什么不同数位上的数字可以相加的道理，由本溯源，解答学生心中的疑惑，让学生感受到数学的奇妙，感受到思考带来的乐趣，感受数学的深度和温度。