基于波利亚“怎样解题表”的解题教学研究*
——以“解三角形”为例
广西师范大学数学与统计学院(541004) 邓新星 莫宗赵 周 莹
乔治·波利亚(George Polya)是世界著名数学家和数学教育家,也是数学解题方法论的开拓者[1].他长期从事数学教学,在数学教育领域有精深的造诣.经过多年的实践与反复修改,他将自己的解题思想凝聚为一张“怎样解题表”.波利亚的“怎样解题表”为数学问题的解决提供了有效的思路,在数学解题教学中应用广泛.鉴于此,笔者以典型的高考真题为例,深入探讨了波利亚的“怎样解题表”在高中数学解题教学中的具体应用.
1 “怎样解题表”的简介
波利亚的“怎样解题表”将整个解题过程分为四个阶段:理解题目、拟订方案、执行方案、回顾,每个阶段又设置了一系列问题启发联想(见表1)[1].

表1 波利亚“怎样解题表”
2 “怎样解题表”在“解三角形”中的应用
例1(2012年全国新课标I 卷, 理科数学, 第17 题)已知a,b,c分别为三角形ABC三个内角A,B,C的对边,(I)求A;(Ⅱ)若a=2,三角形ABC的面积为求b,c.
下面根据波利亚的“怎样解题表”进行求解:
第一阶段: 理解题目
问题(未知): 第(I)问求三角形ABC的内角A,第(Ⅱ)问求边长b,c.
条件(已知):acosC+是整个题目的条件.此外, 第(Ⅱ)问新增了两个前提条件:a= 2 以及三角形ABC的面积为为了方便表示,引入数学符号S1表示三角形ABC的面积,即:S1=
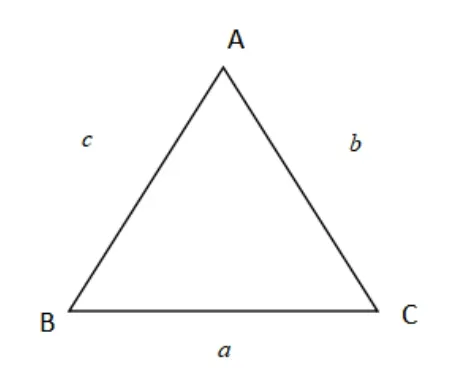
图1
根据题干信息,可画出一张草图(见图1),以便更好地代入问题情境.
第二阶段: 拟订方案
首先,让我们回忆一下,以前是否遇到过类似的题目.本题涉及到的都是三角形的元素之间的某些关系,而“解三角形”指的是从三角形的已知元素求出三角形未知元素的过程.该题符合这一特征,可初步判定: 本题是一道典型的“解三角形”的数学题,考查的是人教A 版必修五第一章的内容.
然后, 联系所学的知识, 可知: 解答此类题目通常需要借助正弦定理、余弦定理以及三角形内角和定理.此外, 本题还涉及到三角形ABC的面积公式:
最后,结合题中的关键信息,拟订以下解题方案:
第二步: 根据三角形的面积公式,并结合已知条件,尝试求出相应的未知量.若不能直接求出最终结果,则再次使用正弦定理、余弦定理或者三角形内角和定理来辅助求解.
第三阶段: 执行方案
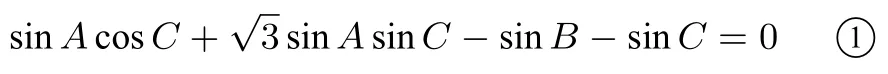
根据三角形内角和定理:A+B+C=π, 移项可得:B=π-A-C,代入①式,整理可得:
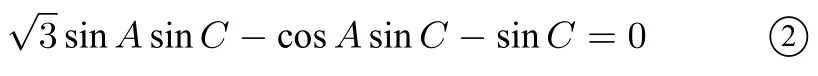
由0< C < π, 可得: sinC /= 0.在②式左右两边同时除以sinC, 得:-cosA -1 = 0, 整理可得:又由0<A <π, 解得:此时,顺利实施了方案的第一步,且完成了第(I)问的解答.由三角形的面积公式:又由解得:

由a=2,bc=4,又由余弦定理a2=b2+c2-2bccosA,整理可得:

因为b,c ∈N*,联立③、④解方程组,可得:b= 2,c= 2.这时,方案的第二步得以顺利实施,且成功解答了第(Ⅱ)问.
第四阶段: 回顾
(1)正面检验结果: 将求出的最终结果代入题干中,完全符合题意.即每一步的推理是有效的,演算是准确的.
(2)在解题方法上,本题同时使用了正弦定理、余弦定理以及三角形的内角和定理进行求解,是一个“解三角形”问题的成功案例.
(3)“有不同方法吗? ”事实上,对于本题的第(I)问,还可以采用其他解法:
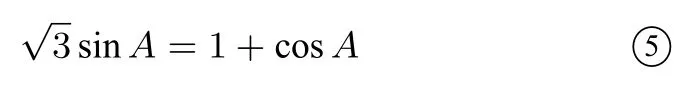
由cosA ∈(-1,1),则: 1+cosA /= 0,在⑤式左右两边同时除以1+cosA,整理可得:根据半角公式:可得:解得:
(4)“能用该结果或方法到其他问题吗? ”这一类型的数学题在高考中经常出现,解题方法大致相同,都是运用正弦定理、余弦定理以及三角形内角和定理进行求解,如例2 所示.
例2(2013年全国新课标Ⅱ卷, 理科数学, 第17 题)三角形ABC在内角A,B,C的对边分别为a,b,c, 已知a=bcosC+csinB.(I)求B;(Ⅱ)若b= 2,求三角形ABC面积的最大值.
解: 理解题目后, 可发现本题的第(I) 问求的是三角形ABC的内角B, 第(Ⅱ)问求这个三角形面积的最大值.第一步, 与例1 的解法一致, 都是先根据已知条件, 结合正弦定理以及三角形的内角和定理, 通过变形来获取新的信息,这时可得:从而完成了第(I) 问的求解.第二步,也是先写出三角形面积的表达式.为了区别于例1, 我们用S2来表示三角形ABC的面积.由于我们知晓的是B,故使用三角形面积公式:代入,可得:又根据已知条件b= 2, 以及余弦定理b2=a2+c2-2accosB, 可得: 4 =a2+c2-由于此题还涉及到最值问题, 我们可以采用基本不等式:a2+c2≥2ac, 故:ac≤(当且仅当a=c时, 等号成立).又由S2=可得:因此三角形ABC面积的最大值为这时,本题的第(Ⅱ)问得以顺利解答.
(5) 回顾整个解题过程, 可用思维导图来构建“解三角形”的知识网络(见图2):
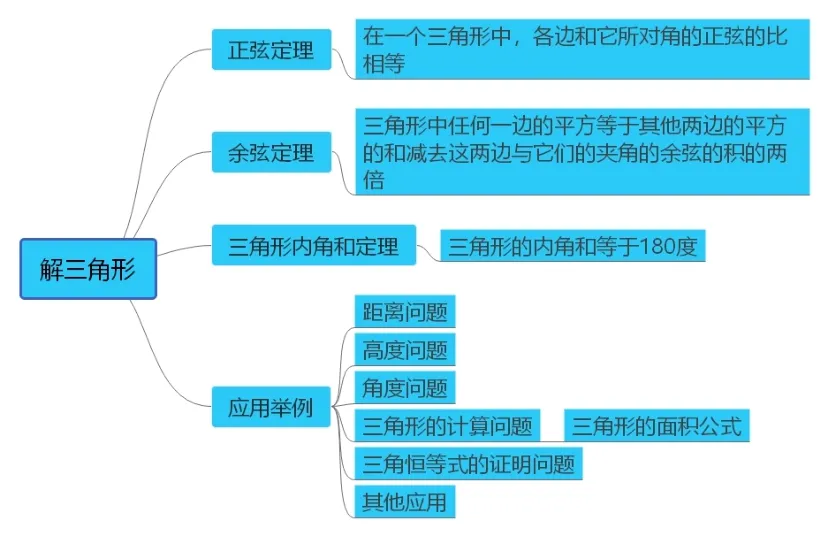
图2 “解三角形”的知识脉络
3 总结与思考
数学的解题活动是一种数学的思维活动[3].波利亚“怎样解题表”中的四个阶段都蕴含着元认知思想[4],自我启发式提问体现出数学思维的层层递进.在数学解题教学中,教师可从以下三个方面加强对学生解题的引导,以培养学生规范的数学思维习惯.
3.1 解题前寻求切入点
认真审题是有效找到解题切入点的前提,也是有力提高解题效率的关键[5].一方面,教师要强化学生的审题意识,引导学生养成良好的审题习惯,即认真细致读题、抓好关键词句以及画出示意图等.另一方面,教师要鼓励学生增强审题的信心,培养学习数学的兴趣.例如,先从数学基础题的审题入手,由易到难,逐渐克服畏难情绪.
3.2 解题时瞄准突破点
首先,教师应重视数学基础知识的讲授.良好的知识储备有利于学生进行知识迁移,从而迅速地找到解题的突破点.然后,教师应着眼于学生的最近发展区,通过启发性的提问,积极引导学生找到数学问题的源头,并及时疏通[5].最后,教师应有针对性地加强学生解题策略的训练,让学生在不断尝试中积累经验,从而提高学生的数学解题能力.
3.3 解题后聚焦反思点
“回顾与反思”是数学解题过程中极为重要的环节,它是解题活动后的“元认知”[6].一方面,教师要引领学生反思解题中所涉及的知识点,进一步加深学生的印象,如利用思维导图来构建系统的知识体系.另一方面,教师要引导学生反思解题的方法,总结不同题型的解题规律,让学生学会举一反三.

