思维导图在初三数学教学中的应用策略探讨*
广东省广州市第一一三中学陶育实验学校(510631) 王 玲
思维导图是表达发散性思维的有效图形思维工具,运用图文并重的技巧,把各级主题的关系用相互隶属与相关的层级图表现出来,学生根据这些链条所串联起来的图形,就能够理清数学各知识点及章节的联系, 发现他们之间的规律,从而进行记忆、学习和总结,逐步地理解和掌握数学的知识并进行运用[1].对于初三数学,思维导图更能够将初三的数学知识和初中一二年级所学的内容串联起来,构造出一系列的思维导图,帮助学生加快初中数学知识的理解以及融汇、贯通, 在有限的时间内, 提高数学学习的效率, 提升学习成绩[2-3].因此,对思维导图如何在初三数学教学中应用进行分析,探究思维导图在初三数学教学和复习中的应用策略是我们当前急需解决的一个问题[4].
目前初三学生对于思维导图已经有了一定的了解,重要的数学知识点之间的联系也有了一定的认识,但当需要用这些知识点联系起来解决问题时他们常显得不知所措.这可能是因为很多学生对初三知识体系掌握的不系统,没有弄懂知识点之间的联系,他们摸不到头绪,找不到解决问题的突破口,提炼不出同种类型题目之间的共性,找不到已知和结论之间的桥梁,导致相同类型的题目他们总是做过再错,错过再做,做过还错的现象.另一方面,很多老师的教学也没有围绕学生的最近思维发展区,只是把各章节知识堆砌零散的教给学生,没有将初中三年学生所学习的新旧知识间搭建和连接起来,也没有让学生经历这些新旧知识搭建、连接的这种体验,从而造成很多学生对于初三数学的知识之间的架构印象不深刻,导致他们的思维单一、僵化,层次不清晰,对于各知识点之间也没有得到有效的拓展[5-7].因此,如果我们将思维导图运用到初三数学教学中, 构造初中数学的知识体系,从宏观上讲解和分析各章、节及知识点的联系和区别,加强学生对初中数学知识的系统学习和运用,能够解决上述问题,从而提高初三数学的教学效率.
综上,为解决当前初三数学教学和学习中的问题,我们将引入思维导图教学工具,将其应用到初三数学的教学、复习及练习等多个环节,并对教学中思维导图应用效果进行反馈.下面我们从转变教学方式、培养学习习惯、提高解题能力等三个方面来阐述和探讨思维导图在初三数学教学中的实施策略和取得的教学效果.
1 运用思维导图,构建以问题为中心的课堂教学方式
思维导图的数学教学要求教学要围绕学生的思维发展来进行,教师教学要立足于学生的已有知识经验,通过创设具体问题情境,启发学生进行思考,必要时教师要建立教学支架帮助学生完成学习任务,让学生通过自我探索发现新问题和新知识.构建问题中心课堂有助于学生主体性的发挥,教学不再以教材为中心,而是以实际问题为中心,通过教师提出问题,引导学生思考问题,组织学生讨论问题并解决问题,最后师生再一起讨论总结,提出新问题,获取新知识[5].在我们运用思维导图构建以问题为中心的整个教学过程中,教师只扮演组织者和引导者的角色,学生才是学习发现的主体.例如在相似三角形单元复习教学中,教师会以以下几个步骤来构建问题中心课堂来开展:
1)教师示范,绘制相似三角形的思维导图;
2)引导学生练习绘制相似三角形的思维导图;
3)学生以小组形式讨论和交流绘图;
4)教师提出问题,学生再讨论和完善构图;
5)课堂讨论和评价,再总结本节知识点和分享学生绘制的思维导图,并引导学生思考与本知识点相关的知识和习题.
结果表明,我们运用思维导图构建的以问题为中心的课堂教学方式是学生非常乐于接受的.学生感觉教学方式比较新颖,其以实际问题为中心的模式,给与了他们更多的独立思考机会,提升了他们学习数学的兴趣和自主学习能力,也提升了他们的创新逻辑思维能力.
通过我们对运用思维导图构建以问题为中心的课堂教学方式的实际教学,还表明,这种教学方式对于帮助学生从整体上系统地提高学习效率和成绩, 正确地学习数学知识,养成数学素养都具有重要的意义.这种教学方式也有助于老师在教学过程中更具有目的性与针对性,有利于帮助学生更加深入地理解教学内容,并使学生在很短的时间内提高数学成绩和数学学习能力,并进一步将这一能力辐射到其他学科的课堂学习中,促进其自身的全面发展.学生做出来的思维导图是具有自己个性化的,通过建立自己的记忆链条打通各个知识点之间的联系,通过思维导图的形式呈现出来,整个知识链接的思路是清晰的.经过一段时间的教学,我们课后通过问卷调查和小组访谈的形式,了解到学生对于这种上课方式是接受的,对于数学的学习是有信心的,学生上课的积极性提高了,学习的效率也提高了.因此,我们认为这种授课方式是适应当前初中数学的学习的.运用思维导图构建问题中心课堂的教学,可以深化知识理解,有效突破重难点,提高教学效率,激发学生的学习热情,提高学生学习的积极主动性和课堂参与度,从而提高课堂效率.
2 运用思维导图,培养学生对知识点进行归纳整理的学习习惯
学会对所学的知识进行归纳、整理,对学生学习数学有很重要的作用,它不仅是学生消化吸收知识的必备过程,也是具备数学素养的重要形式[8].学生对数学知识进行归纳、整理的过程就是学生通过对所学知识的理解,提炼出核心知识,再通过思维导图的形式,把所学知识以自己的方式建立层级链接的过程[9].数学学习的过程本来就不只是学生被动的吸收知识的过程,而是对所学知识通过自己的内化,不断地整理、归纳,不断的纠错改错,从而达到对知识能够灵活的运用,举一反三、触类旁通的过程.只有不断地思考,不断的归纳、整理,不断的反思,才能提升学生的分析能力、整理能力、解题能力、逻辑能力,从而提高学习效率[10].
在运用思维导图进行归纳整理数学知识的教学中,我们对于初三数学的各章、节及知识点都进行了思维导图的绘制和联系,在后期的复习中,又对初中数学所有的知识进行了思维导图的绘制和练习,包括总体框架图、知识体系图、章节联系图、几何图等.从而对初中数学的整个知识体系进行归纳和整理,同时也培养学生利用思维导图进行归纳整理的学习习惯.在运用思维导图进行归纳整理数学知识的教学中,我们首先明确的给学生提出学习的任务,告知学生归纳整理的内容是什么,怎样整理,以何种方式整理.这个过程中我们教师也是边做示范边启发学生思考.如对几何知识的归纳整理,我们在做思维导图示范的过程中,我们会启发学生思考,这种几何图形常见的模型有哪些, 它们有哪些区别与联系,它们存在的背景有哪些,在这些背景下几何图形常见的处理方式有哪些等.
下面我们来举一个利用思维导图结合几何图形进行教学的例子.相似三角形常见的模型有A 字型、8 字型、一线三等角等.其中A 字型就是有一个公共角或相等角的三角形,它又分为正A 字型、斜交型、双垂直型和母子型等;一线三等角又分为一线三垂直和非垂直等角等.此外,相似三角形常与其他几何图形如圆、矩形、函数图形等结合,存在于其几何图形内部,这些几何图形常被称为相似三角形的背景.通过这些知识的梳理,我们指导学生绘制了下图的相似三角形思维导图(图1),从而我们也对相似三角形也进行了归纳、整理.而学生也通过对相似三角形常见模型的归纳整理,对相似三角形有了清晰的认识和理解,并进而对这个知识能够灵活的运用,做到举一反三、触类旁通的效果.

图1
3 运用思维导图,提高学生的解题能力
初三数学复习时我们需要不断的对初中数学的各知识点进行整理、归纳和总结,其最终是为了打开学生解题的思路,从而找到各种类型试题的突破口.思维导图除了能够很好的帮助我们对初中数学各知识点进行系统全面的整理归纳外,帮助我们分析试题和解题.运用思维导图,我们可以清晰的提炼出试题中已知和求证之间错综复杂的联系,轻松找到解题的方法,理清解题的思路,提高解题的效率.通过对我校现九年级学生的教学,我们发现,将思维导图运用到数学的解题中,学生学习数学的积极性、主动性得到了很大的提高,学生对试题的举一反三能力也得到了提升,对于一些逻辑性较高的试题的解题思路也比较清晰了.
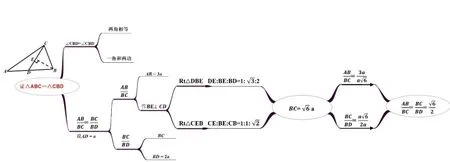
图2
如图2 所示,在ΔABC中,D是AB上一点,且AB=3AD,∠CDB=60°,∠B=75°,求证: ΔABC~ΔCBD.
为更清晰的求证ΔABC~ΔCBD,我们运用思维导图引导学生首先建立以结论为主题的发散导图,再一层层建立记忆链条,并边分析已知边找突破口,直到找到解题的方法(图2).
4 总结
综上,思维导图在数学教学中的应用越来越广泛.将思维导图运用到初三数学的教学中,不仅能够培养学生整理、归纳数学知识的学习习惯,更能提高他们的分析能力、整理能力、逻辑能力,进而提高学生的数学核心素养.老师也能在这一新的教学模式下得到启发,提高课堂教学效率.

