集装箱码头堆场与港前铁路中心站协同调度模型
曾庆成, 吕明蔚
(大连海事大学 航运经济与管理学院, 辽宁 大连 116026)
集装箱海铁联运具有运能大、运输成本低、运输安全性高和污染少等优势,近年来受到越来越多的重视。[1]随着港口的不断发展,对海铁联运的作业效率提出更高的要求。[2]提高节点间的衔接效率对加快海铁联运整体作业效率至关重要。宏观方面,涉及铁路班列规划[3-4]、铁路班列与航线船期表协调[5-6]等;微观方面,涉及港到站集装箱作业顺序优化[7-12]、堆场堆存计划[13-18]、集装箱在铁路中心站和码头堆场中转时机的选择等。
在我国,铁路中心与码头堆场站大多是分离的,增加了海铁联运的作业成本和中转时间。[19]因此,提高码头前沿堆场与铁路中心站的衔接效率成为我国海铁联运运作中的关键因素之一。[2]本文针对上述情况,综合考虑港前铁路中心站与码头前沿堆场2个堆场、箱区作业量和集装箱作业距离等因素,建立进出口集装箱在铁路中心站与码头堆场的协同调度模型。该模型在集装箱到离时间和作业泊位已知的前提下,以堆场箱区之间作业量均衡、集卡作业距离最短、超期集装箱堆存成本最小为目标,优化规划期内海铁联运箱堆存计划。该研究有助于提高港前铁路中心站与码头的协同作业水平,为提高海铁联运作业效率开拓思路。
1 问题描述及建模
1.1 问题描述
本文研究我国港口普遍存在的港前铁路中心站与码头相分离的堆场协同调度问题。协同调度系统作业设施设备见图1。

图1 协同调度系统作业设施设备布局
在协同调度系统中,海铁联运出口箱堆存方式有2种:
1) 先由列车卸至铁路中心站堆场进行堆存,再通过港区集卡运至码头前沿集结。
2) 先由列车卸至港区集卡,再由集卡运至码头堆场堆存,最后运至码头前沿集结。
海铁联运进口箱堆存方式也有2种同出口箱。
本文的问题研究可分为2个阶段。
1) 以减少集装箱在港区内的运输成本和额外堆存费用为目标,判断选择铁路中心站或码头前沿堆场堆存集装箱。
2) 在第1阶段的基础上,平衡各箱区作业量,同时,缩短集装箱的作业总距离,将集装箱均衡分配到各箱区,确定最终的堆存计划。
根据码头工作的连续性特点,选用滚动计划的方法解决本文问题。本文设定3 d为1个计划周期,每天被分为4个时段,3 d共12个时段。
1.2 模型建立
本文研究涉及的集装箱类型有:
1)V型箱,指将被运进堆场堆存的尚在船上等待卸船的进口箱。
2)R型箱,指在堆场上等待装船的出口箱。
3)S型箱,指尚在列车上等待卸车的出口箱。
4)P型箱,指在堆场上等待装车的进口箱。
模型假设包括:
(1) 模型中的集装箱均为同一尺寸;
(2) 所有到发箱全部堆存在箱区,不直装直卸;
(3) 规划期内堆存免费,超出规划期产生堆存费,不足1 d按1 d计算;
(4) 集卡取送箱不存在延误。
1.2.1堆场空间资源配置模型M1
(1) 参数说明:H为堆场集合,h=1为港口堆场,h=2为铁路中心站堆场,h∈H;T为计划周期内计划时段的总数,t为计划周期内第t个计划时段,t=1,2,…,T;k的意义与t相同,k=1,2,…,T-t;M为泊位和班列装卸线的位置集合,m∈M;dmh为泊位(或装卸线)m到堆场h的距离;N为箱区集合;i为具体箱区,i∈N;dh1为堆场h到码头前沿集结区的距离;dh2为堆场h到班列集结区的距离;w为距离的成本系数;αt,m和βt,m分别为t时段m处在计划期外被提走的V型和S型箱量;Qt,h为t时段堆场h的容量;ch为在堆场h中每个超期集装箱每天产生的堆存费;ω为距离相关系数;dmi为m到各箱区i的总距离;Vtk,nh和Stk,mh分别为在t时段由m送进h堆场,在(t+k)时段被提走装车的V型和S型箱量;Rt,hi为在t时段在h堆场i箱区的R型箱量;Pt,hi为在t时段在h堆场i箱区的P型箱量;Rt,0hi为在t时段开始时在h堆场i箱区的R型箱量;Pt,0hi为在t时段开始时在h堆场i箱区的P型箱量;Gt,hi为在t时段堆存在h堆场i箱区的总箱量;qhi为h堆场i箱区的容量。
(2) M1模型决策变量:αt,mh和βt,mh分别为计划时段t时由m送进h堆场,在计划期外被提走的S型和V型箱量;Vt,mh和St,mh分别为计划时段t时由m分配到h堆场的V型和S型箱量;Vt,m和Sf,m分别为计划时段t时m处的V型和S型箱量。第1阶段数学模型为
(1)
(2)
(3)
(4)
(5)
(6)
αt,mh≤St,mh
(7)
βt,mh≤Vt,mh
(8)
Vt,mh,St,mh,αt,mh,βt,mh≥0
(9)
式(1)为目标函数,表示每时段中各类型的海铁联运箱作业距离和超期集装箱堆存成本最小;式(2)~式(5)表示每个集装箱必须存放在1个堆场且只能存放在1个堆场;式(6)表示t时段分配进堆场的箱数不能超过堆场的容量;式(7)和式(8)表示分配到h堆场的计划期外被提走的箱子不能超过分配到该堆场的该箱型的总量;式(9)表示决策变量为非负整数。
1.2.2堆场空间资源配置模型M2
M2模型决策变量:αt,nhi和βt,mhi分别为在t时段由m送进h堆场i箱区在计划期外被提走的S型和V型箱量;Vtk,mhi和Stk,mhi分别为在t时段由m送进h堆场i箱区在(t+k)时段被提走装车的V型和S型箱量;Vt,mhi和St,mhi分别为在t时段由m送进h堆场i箱区的V型和S型箱量。第2阶段数学模型为
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
Gt,hi≤qhi
(22)
St,mhi,Vt,mhi,αt,mhi,βt,mhi,Vtk,mhi,Stk,mhi≥0
(23)
式(10)为目标函数,以堆场箱区作业量均衡且作业泊位到箱区距离最短为目标进行海铁联运箱的箱区分配;式(11)为t时段由m分配到h堆场i箱区的V型箱数量;式(12)为t时段由m分配到h堆场中在(t+k)时段被提走装船的V箱数量;式(13)为t时段由m分配到h堆场i箱区但在计划期外被提走的V型箱数量;式(14)为t时段由m分配到堆场h的V型箱数量;式(15)和式(18)为S型箱约束,含义同V型箱;式(19)为t时段h堆场i箱区的R型箱数量;式(20)为t时段h堆场i箱区的P型箱数量;式(21)为t时段h堆场i箱区的总箱量数;式(22)为容量约束;式(23)为决策变量为非负整数。
2 模型求解
算法的总体思路框图见图2。

图2 算法框架图
2.1 整数规划模型为M1模型
利用分支定界算法计算,求解每时段不同箱型分配到铁路中心站和码头前沿堆场的箱量数(包括正常箱和超期箱)。算法具体步骤如下。
1) 初始化参数。设置b为不等式约束值矩阵,表示每阶段的堆场可用容量,初始值为[LQ1,LQ2],t=2后根据新进和提走箱数进行更新。转入2)。
2) 利用线性规划求解数值,得到X和Z,若为初始值,则转入3),否则转入6)。
3) 判断所得解是否有非整数解。设置检验数h和判断公式。当h=1时,转入4);当h=0时,转入第2.2节1)。
4) 判断是否可分支,对遇到的第1个非整数解进行分支。设置检验数h、J和判断条件,转入5)。
5) 添加关于解的上下界值的新约束条件,进行左右分支,转入1),更新Z值及其上下界。
6) 判断左、右两支解是否符合条件,若存在所得值大于上界等情况,则停止分支,转入7)。
7) 遍历所有非整数解,在得到的所有符合条件的结果中选择最小的Z值及对应的X。
2.2 运用启发式算法[15]计算M2模型
首先,对超期箱和正常箱依次进行分配;然后,将具有最大作业量和最小作业量的箱区在该时段内出场且在规划时段内进场的集装箱重新分配,通过调整这部分正常箱,使各箱区作业量均衡;最后,根据距离分配集装箱的具体堆存位置,算法具体步骤如下:
1) 初始化参数,令t=1,输入当前各箱区相关信息值,转入2)。
2)Aa为箱区当前作业量,α为超期箱数,排序Aa,根据式(13)和式(17)等约束,依次将V型和S型超期箱分配到当前有最小Aa的箱区内,对Aa重新排序。超期箱分配方法见图3。转入3)。
3) 根据相关约束,并结合容量约束,依次将V型和S型正常箱分配到当前Aa最小且未来Aa不是最大的箱区内。正常箱分配方法见图4,Aa计算方法同超期箱。更新箱区容量,令t=t+1,转入4)。
4) 根据距离由远到近进一步确定具体的集装箱分配计划,转入5)。
5) 判断当前时段t,若t≤T,求解目标函数值,转入M1模型6),否则转入M1模型1)。
6) 令t=T,更新当前时段及以前各时段各箱区作业量等信息,并对Aa进行排序,转入7)。
7) 找到当前具有最大作业量的箱区,若该箱区没有分配在以前计划时段进场在当前出场的集装箱,或该时段的出场箱在进场时该箱区具有最小工作量,则转入9),否则转入8)。
8) 将当前具有最大作业量的箱区中在该时段出场且在规划期内进场的集装箱调整到当前具有最小工作量的箱区中,转入7)。
9) 找到当前具有最小作业量的箱区,若当前时段出场的集装箱所在箱区在这些集装箱进场时段具有最小工作量,则转入11),否则转入10)。
10) 将在当前时段出场并且在计划周期内进场的集装箱调整到当前具有最小工作量的箱区中,转入7)。

图3 超期箱分配方法

图4 正常箱分配方法
11) 根据距离由远到近进一步确定具体的集装箱分配计划,令t=t-1,转入12)。
12) 若t<0,则求解目标函数值,输出结果;若t≥0,则转入7)。
3 算例分析
本文基于大连铁路集装箱中心站6条装卸线和大窑湾3期作业区2个泊位某时段实际作业数据(M=8),选择中心站主堆场的4个箱区(单个箱区容量为360 TEU)和大窑湾3期作业区17泊位、18泊位后方对应的4个箱区(单个箱区容量为180 TEU)作为海铁联运集装箱堆存地点(H=2,N=4),在对应布局下,对本文提出的模型和算法进行验证。
以第1计划周期为例,每时段需堆入铁路中心站与码头前沿堆场的箱量见表1。算例在软件MATLABR2018a中进行求解。

表1 第一规划期每时段需堆入堆场的箱量
模型M1目标函数的计算结果见表2,总成本为84 515。若采用港口现有的分配方式,结果最高可达88 300。对比可知:采用该模型可在很大程度上减少集装箱运输成本和超期集装箱堆存成本。
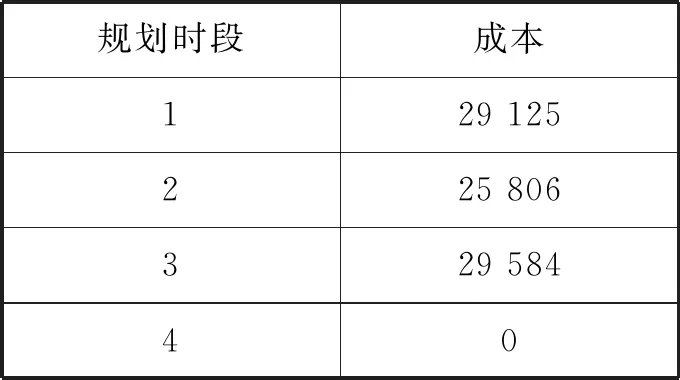
表2 模型1目标函数求解结果
为便于模型M2的后续运算,ω取0.000 1[15],将各箱区与泊位(装卸线)的实际距离转化为[0.001,1.000]区间的数值进行计算,设定的实际距离见表3和表4。

表3 各箱区到泊位的距离 m
在模型M2目标函数的计算结果中,规划期内每个规划时段各箱区的作业箱量的计算结果见图5和图6。
随机堆存与本文堆存方法不平衡箱量的线性对比见图7。由图7可知:铁路中心站和码头堆场不平衡箱量的数量均少于8个;采用现有调度方法,不均衡箱量的数量则不多于20个。由此可知:本文算法比现有经验规则有较大改进,能有效地减少各箱区之间作业量不均衡情况,提高设备、设施的利用率。

表4 各箱区到装卸线的距离
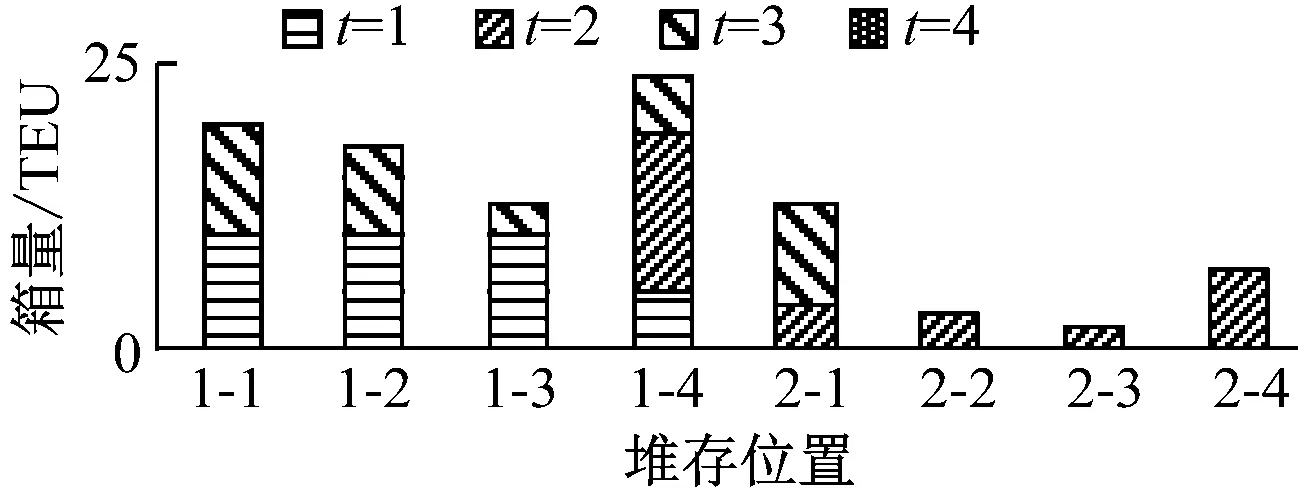
图5 每阶段各箱区入场箱量
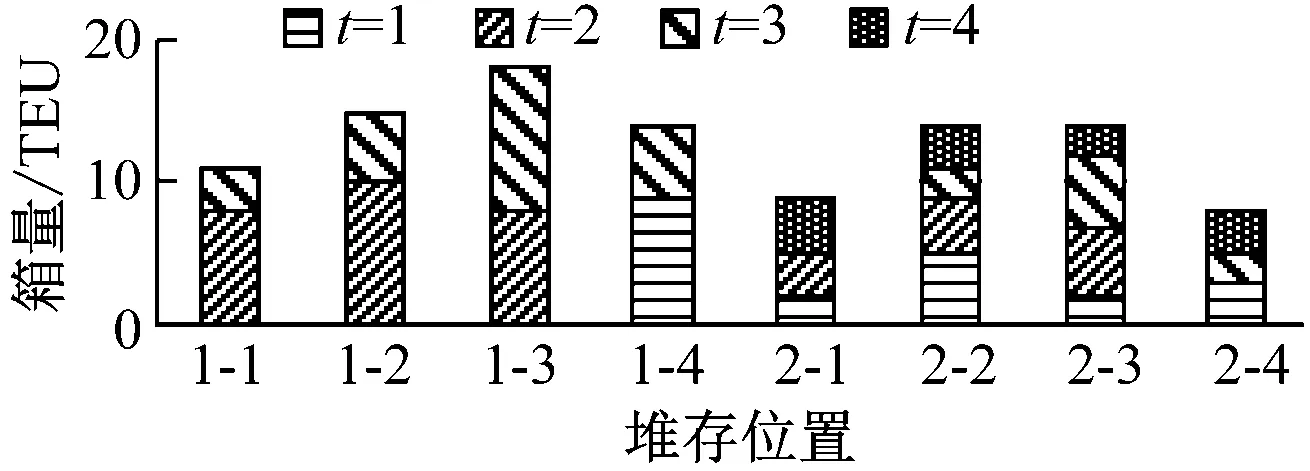
图6 每阶段各箱区出场箱量

a) 铁路中心站堆场
模型M2中有关海铁联运箱作业距离的计算结果为61 260 m;若对上述海铁联运箱随机分配(即在港口现有调度规则下),计算规划期内所有进出口箱作业时的距离总和,得到的最小值为78 420 m,最大值为95 000 m。对比可知:采用本文算法能缩短进出口箱的作业距离。总运行距离缩短证明该算法能缩短装卸船和班列的时间,提高服务效率。
为评价本文模型和算法的性能,对92个计划时段的集装箱堆存作业进行求解。选择各时段箱区作业量的不均衡箱量作为评价指标,将本文求解结果与随机堆存结果相比较,求解结果见图8和图9。

图8 码头堆场不均衡箱量折线图
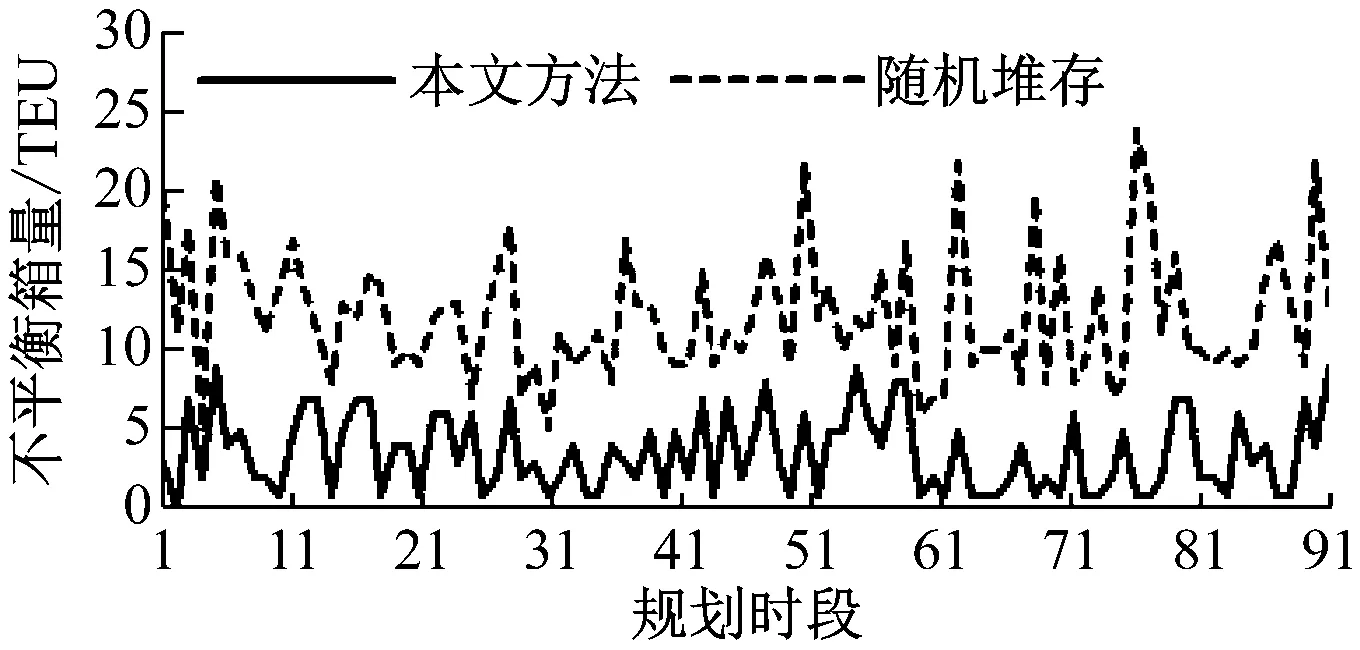
图9 铁路中心站堆场不均衡箱量折线图
由图8和图9可知:在92个计划时段中采用本文方法求得的最大不平衡箱量值比现有的随机堆存方法值小得多。由此可知:本文提出的模型和算法对较大规模的算例同样具有良好的求解性,并在箱量均衡方面较现行方法有改进,能够均衡铁路中心站与码头堆场各箱区之间的作业量,提高协同堆存的作业效率。由于在每个规划期内,铁路中心站和码头前沿堆场的箱区利用率为62.5%~75.0%,因此,不会出现到达集装箱全部堆存在同一箱区的情况,从而提高堆场箱区的利用率。
4 结束语
本文对同时考虑进口和出口集装箱的港前铁路中心站与码头前沿堆场的协同调度问题进行研究。以箱区之间作业量均衡、集装箱作业总距离最短和超期堆存成本最少为目标,建立集装箱在铁路中心站与码头堆场协同调度的2阶段模型,并设计启发式算法求解规划期内海铁联运箱堆存计划。算例验证结果表明:该模型和算法能将V型、S型箱均衡地分配到各箱区,缩短作业总距离,优化铁路中心站与码头前沿堆场的协同堆存问题,提高堆场的利用率,节约总成本。

