HUUSKA/GULIEV公式挖槽式航道修正系数的连续回归模型
陈丽宁, 神和龙
(1.广州航海学院 海运学院, 广州 510725; 2.大连海事大学 航海仿真与控制交通行业重点实验室, 辽宁 大连 116026)
运动中的船舶由于流过船体的水流速度增加,作用于船体的压力减小,造成船舶下沉并伴有纵倾。[1]船舶下沉会减少船舶安全富余水深、降低船舶操纵性,可能造成船舶触底、搁浅。船舶驾驶员、引航员、海事监管人员、船舶设计人员和航道设计人员等[2]通常使用船舶下沉量经验公式计算船舶下沉量,其使用不当可能导致计算结果误差较大。HUUSKA/GULIEV公式是一种适用于计算天然水深航道、挖槽式航道和运河式航道船舶下沉量的经验公式,国际航运协会(World Association for Waterborne Transport Infrastructure, PIANC)和芬兰交通设施局(Finnish Transport Infrastructure Agency, FTIA)均推荐在航海实践、通航安全评估和航道设计中使用该公式。
TUCK[3]采用细长体理论计算静水中航行船舶的下沉量,并给出船舶下沉量经验公式,即TUCK公式,其有复杂的积分项,给使用带来不便。HUUSKA[4]和GULIEV[5]将Tuck公式与试验观测数据结合,提出HUUSKA/GULIEV公式,其包含挖槽式航道修正系数,但HUUSKA和GULIEV仅给出该系数的曲线,却未给出该系数的函数。PIANC[6-7]参考该曲线给出该系数的35个离散值。BRIGGS[8]对这些离散值进行回归分析,给出5个挖槽水深和航道水深比值(简称水深比)的船舶下沉量回归模型。FTIA[9-10]将该系数函数的定义域分为5个子域,在每个子域中使用相应的Briggs回归模型,当船速较低、弗劳德数较小时,用细长体理论计算船舶下沉量较准确。[2,11,12]HUUSKA/GULIEV公式来源于细长体理论,其计算结果应与细长体理论数值的计算结果接近。比较发现:使用FTIA模型可能导致HUUSKA/GULIEV公式挖槽式航道下沉量计算结果与细长体理论数值计算结果相差较大。有些研究虽使用HUUSKA/GULIEV公式,但并未明确给出挖槽式航道修正系数的计算方法。
针对上述问题,本文对HUUSKA/GULIEV公式挖槽式航道修正系数进行回归分析,提出该系数的连续回归模型。首先以阻塞系数、水深比为坐标的非均匀网格变换为均匀网格,在均匀网格下进行回归分析,估计回归参数并检验其显著性,根据显著性检验结果对回归模型进行改进,剔除线性相关性较弱的回归变量。对改进后的回归模型进行适用性检验,发现残差不服从正态分布,该模型具有不适用性,需进行方差稳定化变换。经方差稳定化变换后的模型的残差服从正态分布,模型的不适用性得到修正。本文模型的计算结果比FTIA模型的计算结果更接近于细长体理论数值的计算结果,精度更高,验证该模型的有效性。本文模型比细长体理论数值计算更简捷并便于在工程领域中应用。
1 问题的提出
1.1 HUUSKA/GULIEV公式
HUUSKA/GULIEV公式可用于计算天然水深航道、挖槽式航道和运河式航道的船舶下沉量。HUUSKA/GULIEV公式为
(1)
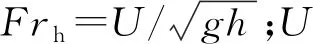
(2)
式(2)中:s1为无量纲修正阻塞系数。对于挖槽式航道
s1=S/K1
(3)
式(3)中:K1为挖槽式航道修正系数,无量纲;S为阻塞系数,其计算为
(4)
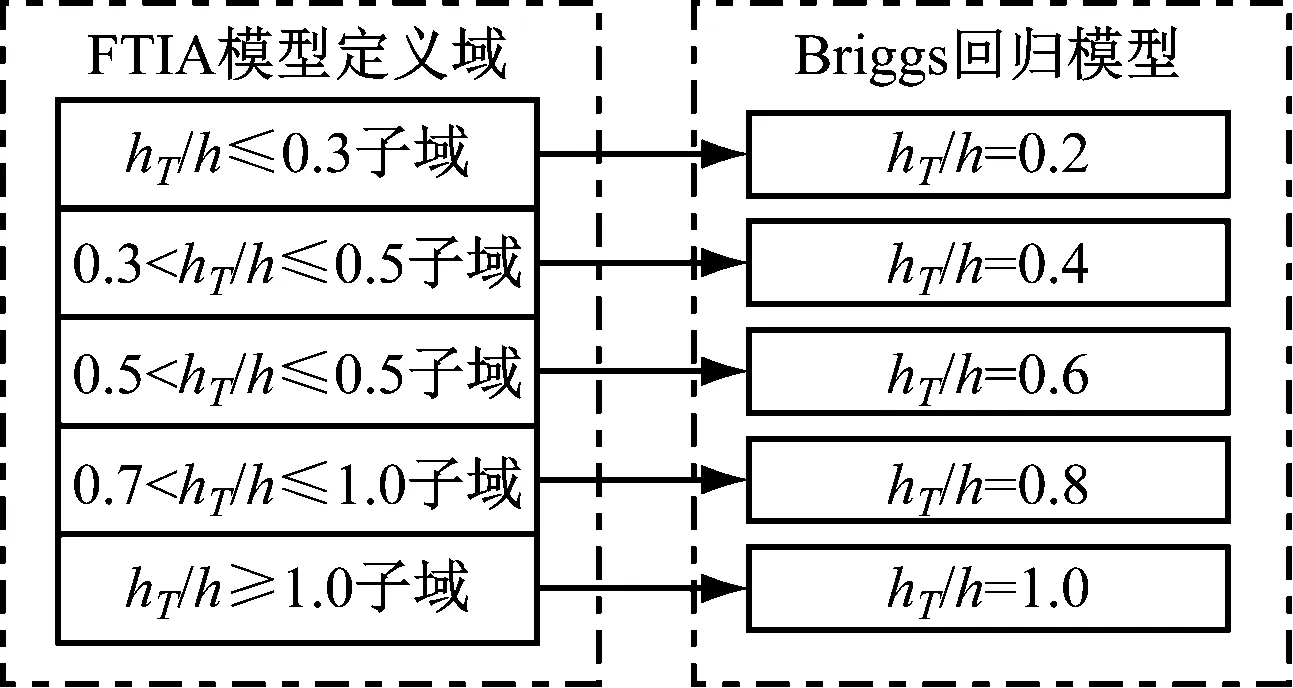
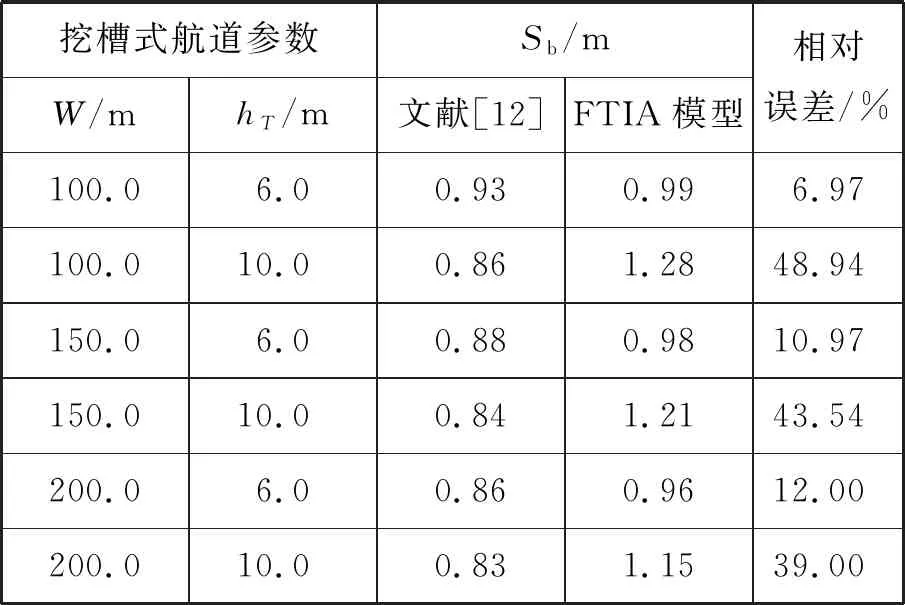
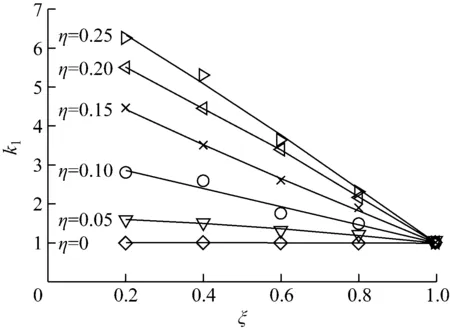
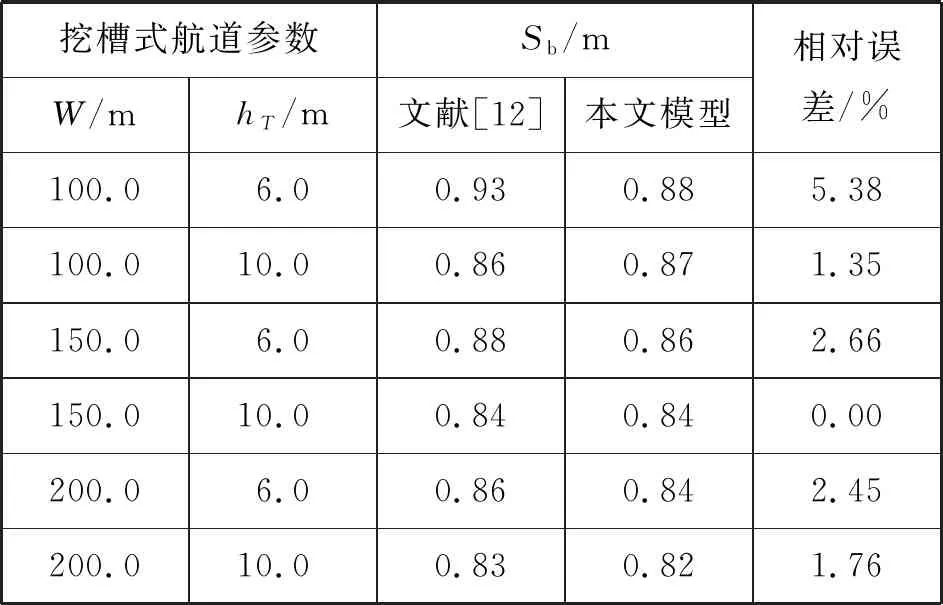
式(4)中:W为航道底宽;n为航道边坡坡度倒数。HUUSKA[5]和GULIEV[6]给出K1的曲线图,但未给出K1的函数。PIANC[7-8]参考该曲线图给出K1的35个离散值,见表1。表1中hT为挖槽式航道的挖槽深度。由表1可知:当0.00≤S≤0.03,K1≡1.00,K1值不受S和hT/h的影响;当0.03 表1 K1的离散值 文献[8]对K1进行回归分析,认为当hT/h为定值时,K1为 (5) 1) 仅给出5个hT/h值K1的回归模型,实际应用中可能需要计算其他hT/h值的K1。 2) 文献[8]使用最小二乘法估计回归参数,但既未给出显著性检验结果和模型适用性检验结果,也未提及拟合结果是否满足最小二乘法的基本假设、模型的稳定性和精度。 表2 Briggs回归模型的R2和的值 FTIA[10]和GOURLAY[11]将K1函数的定义域分割为5个子域,在每个子域中使用相应的Briggs回归模型。FTIA模型子域与Briggs回归模型关系图见图1,FTIA模型在每个子域内连续,相邻子域交界处间断,即FTIA模型分段连续。 图1 FTIA模型子域与Briggs回归模型关系图 为验证FTIA模型的精度,需将该模型计算结果与试验结果进行比较。研究人员为研究浅水航行船舶的下沉量进行一系列试验,包括水池试验、实船试验和数值试验。目前,水池试验对运河式航道开展较多,对挖槽式航道开展较少。MOCTAR等[11]给出挖槽式航道水池试验数据,但试验的水深Fr超出HUUSKA/GULIEV公式适用范围,试验结果不适合作为比较对象。GOURLAY[12]开发的Shallowflow软件实现细长体理论数值计算,并进行数值试验,其条件也符合HUUSKA/GULIEV公式的要求,因此,选择GOURLAY的数值计算结果作为比较对象。 数值试验所用船体为S1704B散货船,该船体有球鼻艏,Lpp=174.0 m,B=32.2 m,T=12.0 m,CB=0.801,U=10.0 kn。令h=14.0 m,n=4.0,挖槽式航道参数和数值计算结果见表3。由表3可知:当hT/h较小时,文献[12]数值计算结果与FTIA模型计算结果相差较小,FTIA模型精度较高;当hT/h较大时,文献[12]数值计算结果与FTIA模型计算结果相差较大,FTIA模型精度较低。FTIA模型用某一特定hT/h值的Briggs回归模型表征该hT/h值所在子域的回归模型,这导致在hT/h较大时计算不准确,误差较大。要解决该问题,需要运用新的回归模型,该模型应连续,经过显著性检验、模型适用性检验表明模型的精度较高,计算结果与细长体理论数值计算接近。 表3 挖槽式航道参数和数值计算结果 由表1可知:当0.03≤ΔS≤0.25、0.2≤hT/h≤1.0时,Δ(hT/h)≡0.2,ΔS为非定值,坐标(hT/h,S)的网格为非均匀网格。为便于计算,可考虑将非均匀网格变换为均匀网格。为此,引入变量ξ、η,有 ξ=hT/h,有 (6) 式(6)中:Δξ≡0.20,Δη≡0.05,坐标(ξ,η)的网格为均匀网格。均匀网格既便于计算机编程实现,也便于使用回归分析、有限差分和牛顿差值等数学方法。将K1的回归模型表达式写为连续形式 (7) 需要注意的是不应使n、m过大,避免表达式的阶数过高。由式(5)可得,当n=3时,下一步需要确定m的取值。由式(7)可得,当η为定值时,K1的回归模型为 (8) 绘制η为定值、ξ为变量的散点图见图2,由图2可知:当η为定值时,K1与ξ近似线性相关,则令m=1,用最小二乘法进行参数估计,并对模型进行回归显著性检验,以验证K1和ξ是否存在强线性相关关系。回归显著性检验为 H0:β1=0,H1:β1≠0 (9) 检验所用统计量为 (10) 图2 η为定值的散点图和回归直线图 表4 η为定值的和|t0| K1=Xβ (11) 式(11)中: (12) (13) 多元回归相关系数为 (14) 一般而言,向一个模型中增加一个回归变量时,无论这一变量的贡献值如何,R2不会下降。因此,多元回归中通常采用调整后的相关系数RAdj (15) (16) 检验βij,多元回归显著性假设为 H0:βij=0,H1:βij≠0 (17) 如果不能拒绝H0,则表明ηiξj线性相关性不强,βij=0。检验所用的统计量为 (18) 表和tij的值 K1=β00+β20η2+β30η3+β21η2ξ+ β31η3ξ+ε (19) 表6 剔除线性相关性不强回归变量后的和tij的值 显著性检验可检验响应变量与回归变量之间的线性相关性,但不能检验误差是否符合正态分布和回归模型拟合的优劣。误差符合正态分布是回归分析的假设之一,如果模型严重违背回归分析的假设,则模型不稳定。要检验误差是否符合正态分布和模型拟合的优劣,需进行模型适用性检验。如果模型适用性检验没有通过,还需修正模型的不适用性。 用W检验来检验假设H0的步骤如下 1) 将ei按升序排序e[1]≤e[2]≤,…,≤e[nsp]。 2) 计算检验的统计量 (20) 用正态概率图寻找模型不适用性的修正方法。外部化学生残差为 (21) (22) 计算eti值,按升序排序et[1]≤et[2]≤,…,≤et[nsp],进而计算et[i]的累积概率Pi,绘制正态概率图见图3。由图3可知:累积概率为重尾分布,误差的方差不是常数,可采用方差稳定化变换来修正模型的不适用性。[18] 图3 正态概率图 (23) 表和tij的值 本文提出的回归模型可计算船舶下沉量,船舶、航道参数与表3一致,计算结果见表8。当hT=10.0 m、h=14.0 m时,FTIA模型计算结果与细长体理论数值计算结果差别较大。W=100.0 m、150.0 m和200.0 m,FTIA模型的相对误分别为48.94%、43.54%和39.00%,本文模型的相对误差分别为1.35%、0.00%和1.76%,明显小于FTIA模型。当hT=6.0 m和h=14.0 m时,虽然FTIA模型计算结果与文献[12]的计算结果较接近,但本文模型的相对误差更小。显然,与FTIA模型相比,本文模型计算结果更接近文献[12]的计算结果,精度更高。 表8 挖槽式航道参数和本文模型计算结果 HUUSKA/GULIEV公式是基于细长体理论提出的船舶下沉量经验公式,包含挖槽式航道修正系数。FTIA给出挖槽式航道修正系数的分段连续模型,但FTIA模型计算的挖槽式航道船舶下沉量与细长体理论数值计算的船舶下沉量差别较大。针对这一问题,对HUUSKA/GULIEV公式挖槽式航道修正系数进行回归分析,给出该系数的连续回归模型。用最小二乘法估计模型的回归系数,检验回归系数显著性,根据检验结果确定回归模型表达式的形式。在此基础上进行模型适用性检验,发现模型的残差不符合正态分布,模型存在不适用性,需进行方差稳定化变换。方差稳定化变换后模型的不适用性得以修正,模型拟合度良好,与FTIA模型相比,本文模型计算结果更接近于细长体理论数值计算结果,精度更高;本文模型形式简单,计算量比细长体理论数值计算更小,易于工程应用。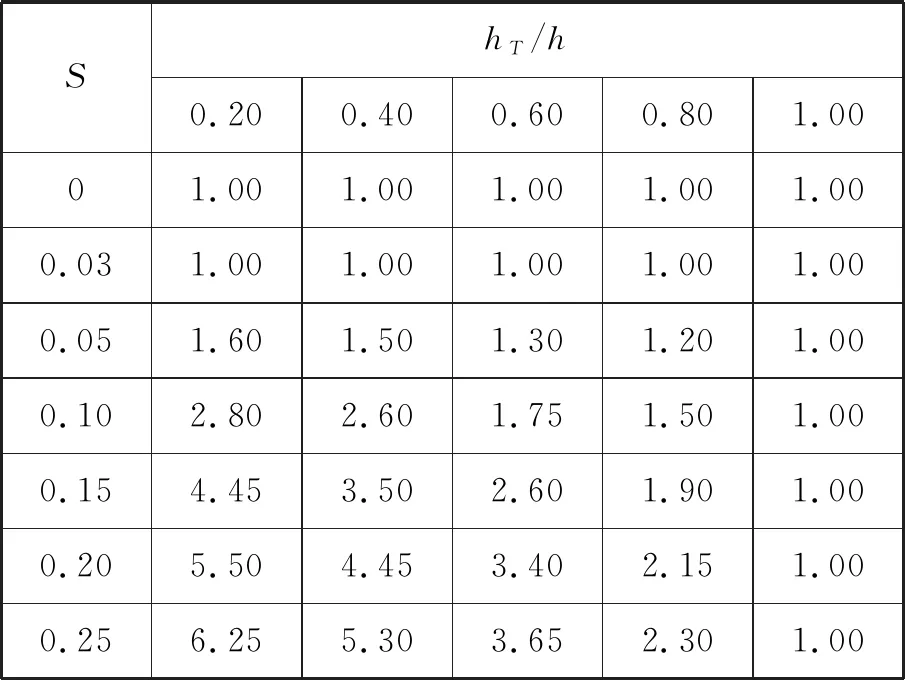
1.2 K1的计算模型-Briggs回归模型和FTIA模型
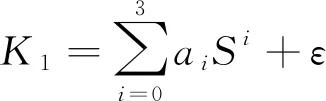
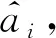
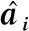
1.3 FTIA模型与细长体理论数值计算结果的比较
2 连续回归模型表达式形式的确定
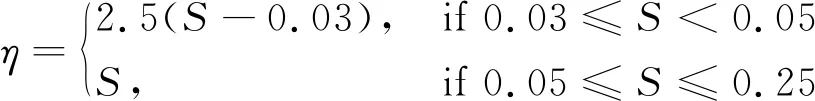
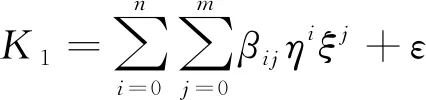
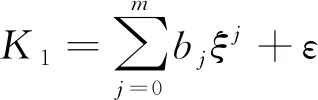
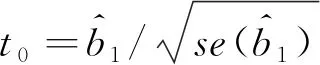
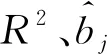
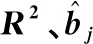
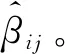
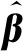
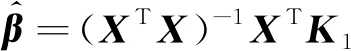
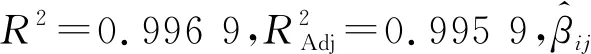
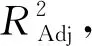


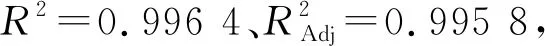
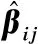
3 模型适用性检验及不适用性的修正
3.1 模型适用性检验
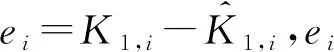
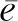
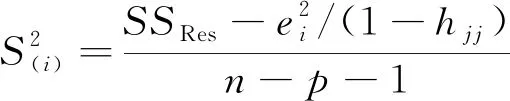
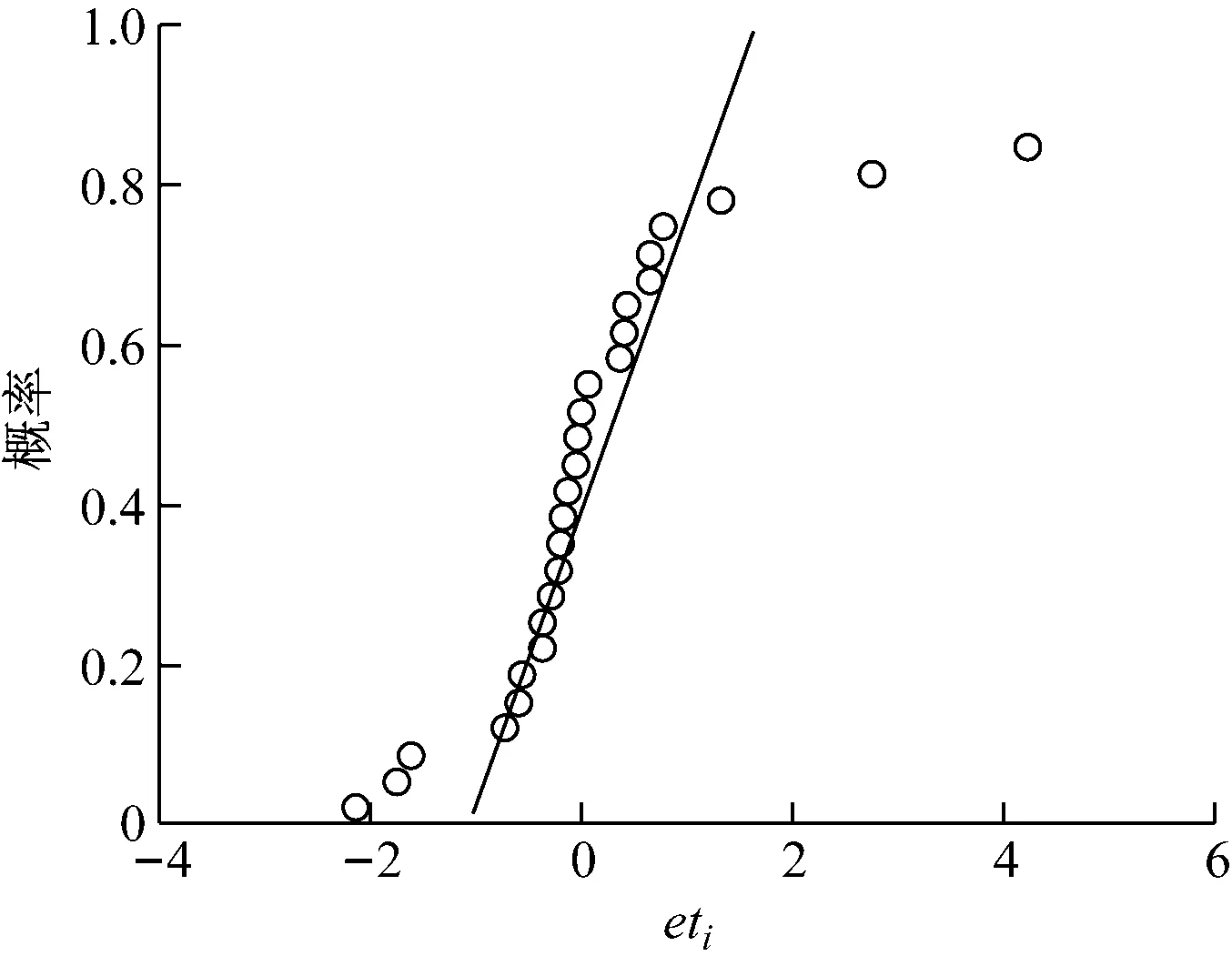
3.2 模型不适用性的修正-方差稳定化变换
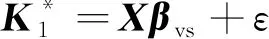
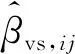
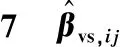
4 计算结果比较
5 结束语

