LNG罐箱运输船罐箱水运破损概率

吴宛青， 蔡昊成， 宋学明

(大连海事大学 轮机工程学院， 辽宁 大连 116026)

近年来，随着人们的环保意识不断增强，天然气这种清洁能源的需求日益增长，天然气运量逐年增加。天然气罐箱整船运输所具备的灵活、低成本和标准化等特点使得其在降低行业门槛、消除垄断、拓展液化天然气(Liquefied Natural Gas, LNG) 中小型用户和促进资源充分利用等方面具有其他运输方式不可比拟的优势。[1]目前，天然气罐箱运输尚处于试点阶段，海事管理机构尚未颁布LNG罐箱装载规范，对罐箱与罐箱之间、罐箱与舷侧之间的距离没有明确要求。通过计算LNG罐箱运输船在航行过程中发生碰撞时罐箱发生破损的概率，可在不同的罐箱装载距离要求下，对LNG罐箱运输船与传统C型舱天然气运输船的安全性进行比较，以确定罐箱与舷侧之间的距离达到某个值时，罐箱运输船与C型舱运输船具有相近的储罐破损概率，为海事部门罐箱装载规范的出台提供理论依据。

国内外已有较为丰富的船舶碰撞相关研究成果，对船舶碰撞问题进行深入研究。PEDERSEN等[2]推导出基于刚体力学的闭式分析解决方案，用于估算任意位置和角度船舶结构受到碰撞变形时所吸收的能量，并根据PETERSEN[3]的模拟进行验证。BROWN[4]通过更先进和全面的时域模拟，证实文献[2]方法的准确性。PILL等[5]通过建立一种有限元模型耦合外部动力学和内部力学的船舶碰撞过程，以便表示船舶运动与结构变形的相互作用，该方法中一些参数的选取还需与试验相结合，作进一步的研究。文献[6]提出采用蒙特卡洛法对船舶通航情况进行统计模拟的思路。本文首先采用有限元法对船舶碰撞过程进行仿真模拟，确定各算例中LNG储罐破损时被撞船吸收的能量，拟合临界破损能量计算式；随后采用蒙特卡洛法，结合实际长江的船舶通航数据，计算在不同区段的不同情况下，船舶LNG储罐的破损概率，对罐箱装载距离的安全性进行比较。

1 理论基础

1.1 变形基本理论

本文采用ANSYS软件对船舶碰撞进行有限元模拟，据此计算临界破损能量，通过一系列算例回归得到船舶破损临界能量的计算式。该软件基于以下基本理论对船舶结构变形进行分析计算。[7]

1.1.1物体运动的描述

在运动系统中，一个可看作质点的物体在t=0时刻所处的空间位置为A点，经过时间t运动到B点。用拉格朗日法对物体在t时间内的运动过程进行描述，有

xi=xi(Xi,t)，i=1,2,3

(1)

式(1)中：xi为B点坐标；Xi为A点坐标。

1.1.2守恒方程

1.1.2.1 质量守恒方程

采用拉格朗日法构建的质量守恒方程为

ρ=Jρ0

(2)

(3)

式(2)和式(3)中：ρ为当前的质量密度，kg/m3；J为体积变化率；ρ0为初始质量密度，kg/m3；V0为初始体积，m3；V为当前体积，m3。

1.1.2.2 动量守恒方程

(4)

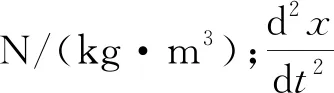
1.1.2.3 能量守恒方程

(5)

式(5)中：E为当前能量，J；V为当前体积，m3；ξij为应变张量；Sij为偏应力张量，N/m3。

Sij=σij+(p+q)δij

(6)

式(6)中：p为压力，N；q为体积黏性阻力，N；δij为δ函数(δij=1，i=j；δij=0，i≠j)。

1.2 材料模型和失效准则

1.2.1弹塑性模型

弹塑性模型是一种可同时反映材料的弹性和塑性的材料模型。当材料承受的应力小于其屈服应力时，材料承受的应力与材料的应变呈线性关系；当材料承受的应力大于屈服应力时，材料发生塑性变形。

船舶碰撞的过程其实就是船体材料在外力的作用下产生变形的过程，在该过程中，船舶结构材料承受的应力会迅速超过其屈服极限，进入塑性变形阶段，过程可用弹塑性材料模型很好地体现，弹塑性材料的本构模型方程为

(7)

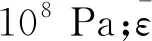
1.2.2材料失效准则

在进行有限元模拟时，材料的失效表现就是所在单元的删除。失效应变一般在0.01～0.20内取值，根据已有研究，参考文献[8]的研究经验，材料失效应变取0.15。

2 临界破损能量的计算

2.1 目标船舶的选取

文献[9]和文献[10]中的数据显示：散货船在长江干线船型中的占比始终超过50%，是长江干线过闸主力船型，撞击船因此选择在长江中广泛通航的3 000吨级、10 000吨级和30 000吨级船舶，船舶尺度参考《长江干线通航标准》[11]和《海港总体设计规范》[12]中的散货船的代表船型尺度，并结合实际船舶尺度选择，具体参数见表1。

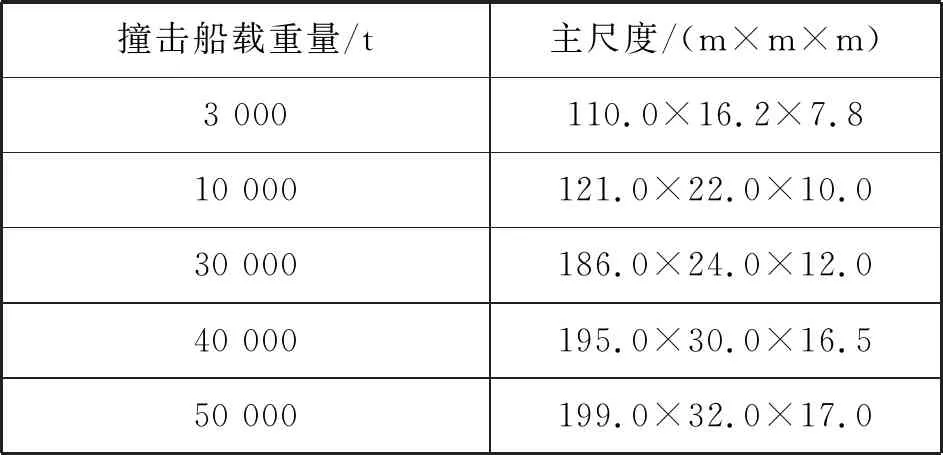
表1 撞击船主尺度

基于长江船舶的通航情况，选择主尺度相似的12 000 m3LNG运输船和1 400 TEU集装箱船作为有限元模拟的被撞船。船舶碰撞能量与船舶尺度有直接关系，因此，对每种船舶分别建立尺度为80%、100%和120%的船舶模型，以得到不同船舶尺度下的吸能情况，船舶的尺度数据见表2。

表2 被撞船的主尺度参数

2.2 船舶模型尺寸的计算与简化

根据中国船级社《钢制内河船舶建造规范》[13]的要求：当船长小于50 m时，肋骨或纵骨间距应不大于600 mm;当船长大于等于50 m时，肋骨或纵骨间距应不大于700 mm。

舯部船底板的厚度T应不小于按式(8)计算所得值为

T=a(αL+βs+γ)

(8)

式(8)中:L为船长，m；s为肋骨或纵骨间距，m；a为航区系数，A级航区取1.00，B级航区取0.85，C级航区取0.70；α、β和γ为系数，其取值见表3。

表3 系数α、β和γ的取值

舯部和过渡区域舷侧外板厚度应不小于船底板厚度计算值的0.9倍。综合考虑以上各因素为减少工作量，提高效率，本文假设船舶各部分钢板的厚度相等，将船舶结构简化为舷侧结构和双层底，取1.2倍船舶模型钢板厚度为17 mm，1.0倍船舶模型钢板厚度为14 mm，0.8倍船舶模型钢板厚度为12 mm。对受力较小的一些船舶结构进行省略处理，例如腹板、小肋板和肘板等。在实际的船舶中，一般每3～4个肋位设置1个强肋板，为简化建模过程，将撞击过程中受力很少的肋骨省略，仅建立强肋板。根据第2.2节的内容，肋骨间距取700 mm，因此在模型中每2.1 m设置1个强肋骨。

2.3 临界破损能量计算式

在实际的LNG罐箱运输中，目前，按距舷侧为760 mm进行装载，通过在天津海事局进行调研可知:海事部门接下来准备将罐箱与舷侧的装载距离要求增加至1个箱位，即2 400 mm。因此,在进行有限元碰撞模拟时，分别采取撞击船侵入被撞船760 mm和2 400 mm作为临界状态；LNG运输船的临界状态选取为船体内壳发生破裂的临界时刻。这样选取的原因是C型LNG储罐为防止热胀冷缩的影响，其鞍座通常只在一侧设置刚性支撑，另一侧为滑动支撑，这种结构在有限元计算中建立模型比较困难。因此,本文选取撞击船的艏部触碰到储罐的时刻作为临界状态，并计算此时被撞船吸收的能量，有限元计算结果见表4～表6。

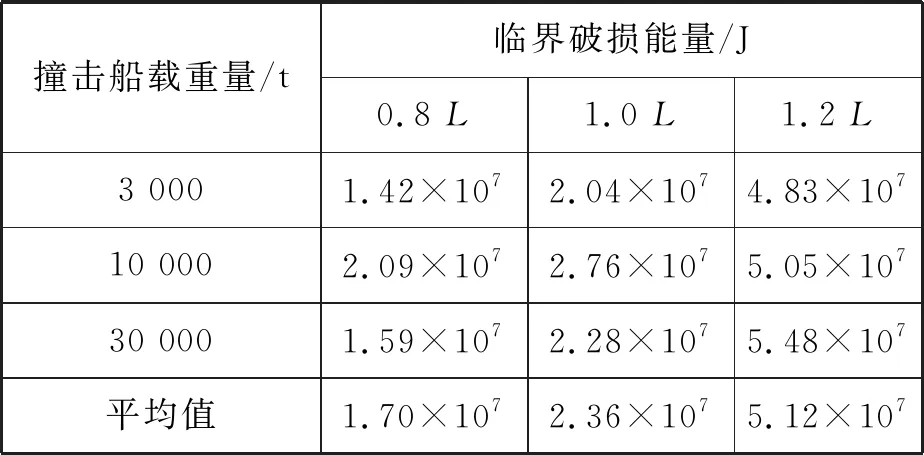
表4 LNG运输船货罐临界破损能量

表5 集装箱运输船LNG罐箱临界破损能量(距舷侧760 mm)

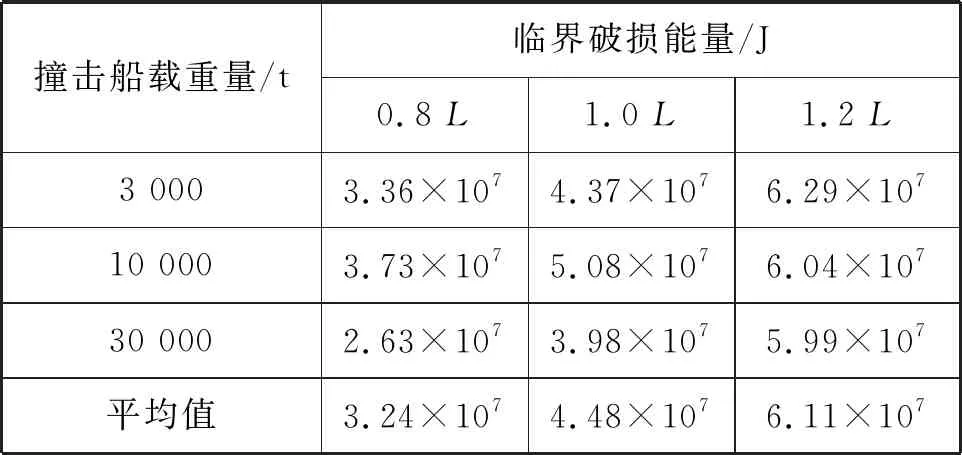
表6 集装箱运输船LNG罐箱临界破损能量(距舷侧2 400 mm)

根据计算的临界破损能量值，对这些数据进行拟合，得到的曲线和表达式见图1。由图1可知：当天然气罐箱按2 400 mm装载时，天然气罐箱的临界破损能量最大；当天然气罐箱按760 mm装载时，天然气罐箱的临界破损能量最小；天然气运输船储罐的临界破损能量在二者之间。

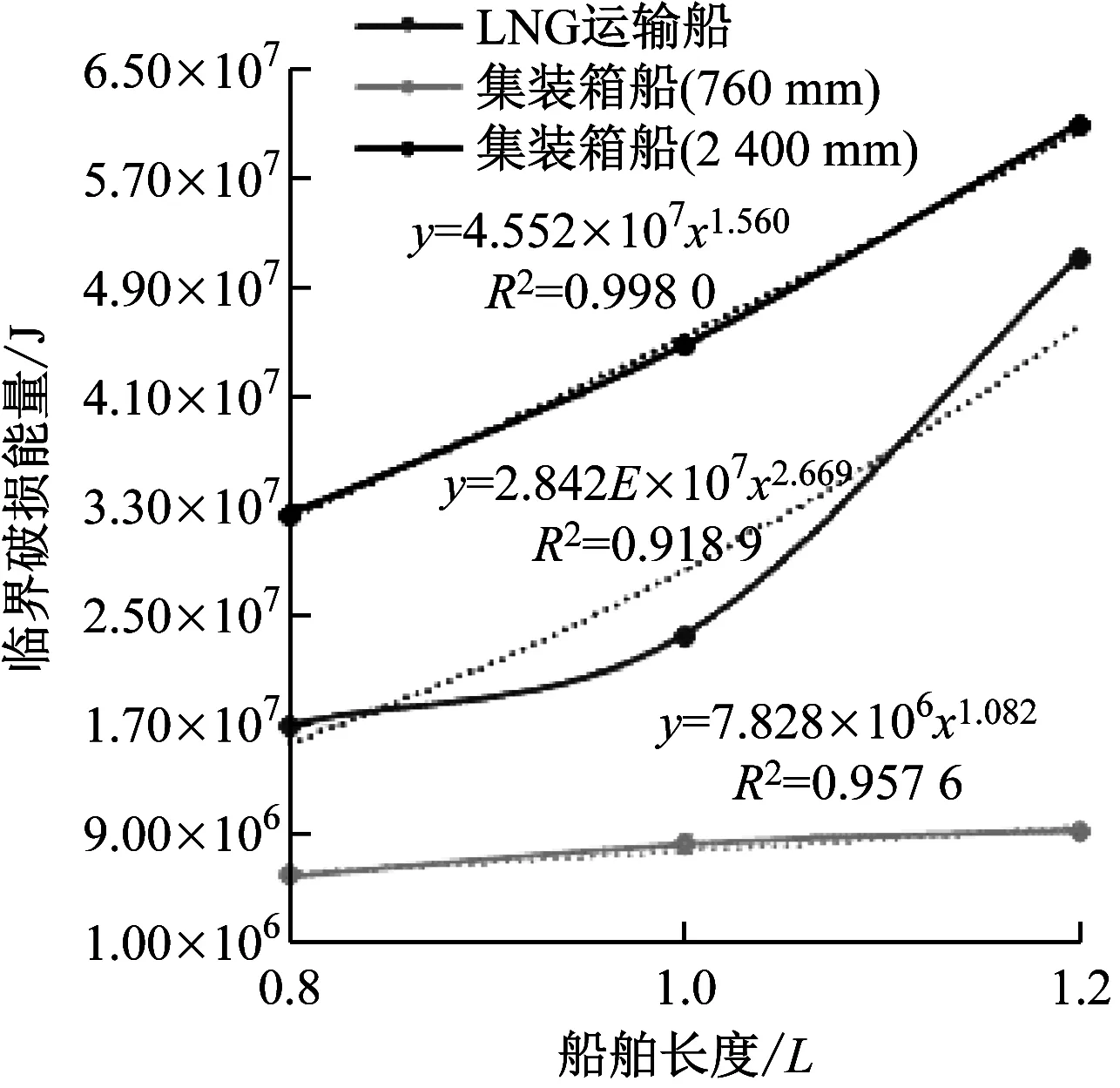
图1 临界能量拟合曲线

LNG运输船天然气储罐的临界破损能量为

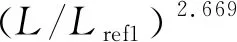
(9)

集装箱船LNG罐箱(距舷侧760 mm)的临界破损能量为

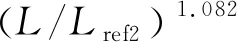
(10)

集装箱船LNG罐箱(距舷侧2 400 mm)的临界破损能量为

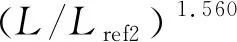
(11)

式(11)中：L为船舶长度；Lref1和Lref2分别为有限元法选取的LNG运输船和集装箱运输船的船长，Lref1=152.3 m，Lref2=169.9 m。

3 储罐破损概率的计算

3.1 蒙特卡洛法概述

蒙特卡洛法又称随机抽样法或统计试验法，是一种使用随机数(或伪随机数)的数值计算方法。在概率统计理论的基础上，利用计算机进行模拟也就是使用统计试验对未知量进行求解。

以在长江中航行的船舶发生碰撞事故为例，在此过程中，被撞船和撞击船的航行速度均是在一定范围内波动的变量，在不同区段、不同时间内船舶航行的速度一般不同，撞击船与被撞船发生撞击的角度和碰撞位置一般也不同，对于含有随机因素的问题，一般难以通过确定模型进行分析，因此可采用蒙特卡洛法。

3.2 储罐破损概率计算流程

采用蒙特卡洛法模拟计算船舶发生碰撞时的破损概率可分为3个步骤：

1) 确定各输入参数的统计分布。

2) 计算被撞船在碰撞过程吸收的能量值。

3) 判定LNG储罐是否发生破损。

输入参数包括所计算区段中的船型、船舶尺度(船长L、船宽B和吃水T)的统计分布，船舶航行速度的统计分布，2艘船舶之间发生碰撞的撞击位置和撞击角度等。要确定这些参数的分布，可在文献[12]中长江中下游流域船舶交通情况统计数据的基础上，通过进一步筛选获得。计算碰撞吸能可选用文献[2]根据船舶外部动力学推导的吸能计算模型，该模型为基于刚体运动力学所建立的吸能模型，不依赖于所研究船舶的船体结构进行计算。利用第2.3节得到的储罐临界破损能量作为判定标准，对储罐是否发生破裂进行判断，由此即可编写计算程序进行蒙特卡洛计算。在每个计算循环中随机生成一个船舶碰撞情景，计算被撞船在该情境下的吸能值，并判定LNG罐箱和货罐是否安全。通过大量的模拟计算，由此得到LNG罐箱和货罐失效的统计概率。

3.3 船舶会遇状态的确定

3.3.1船舶航行速度

在蒙特卡洛模拟中，船舶航行速度是一个重要的输入变量，直接影响撞击船所具有的能量大小。文献[14]对长江中下游船舶交通情况进行观测，统计长江中下游上行船和下行船船速的分布情况，具体数据见表7，本文取该数据作为蒙特卡洛模拟中的船速输入。

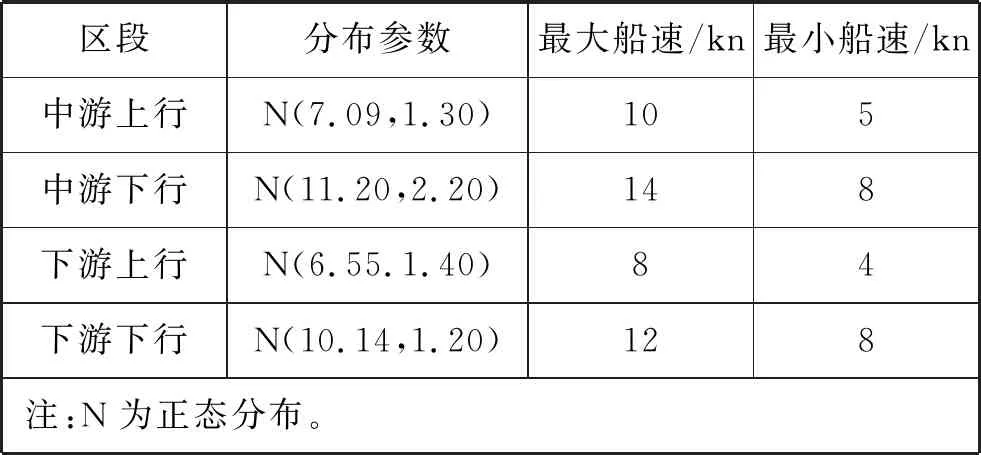
表7 长江中下游船舶航行速度分布

3.3.2船舶长度

根据海事主管部门提供的数据，长江中下游船舶长度分布见表8。

根据表8中的船舶长度分布，选取每个区段中船长处在中位数的船舶代表该分段，代表船舶尺度见表9。以表8和表9中的数据作为计算程序中撞击船生成的依据。被撞船采用有限元计算中选取的目标船，在编写程序时将被撞船的尺度随机缩放0.8～1.2倍，由此模拟不同尺度的船型在长江中下游航行时发生碰撞的情况。

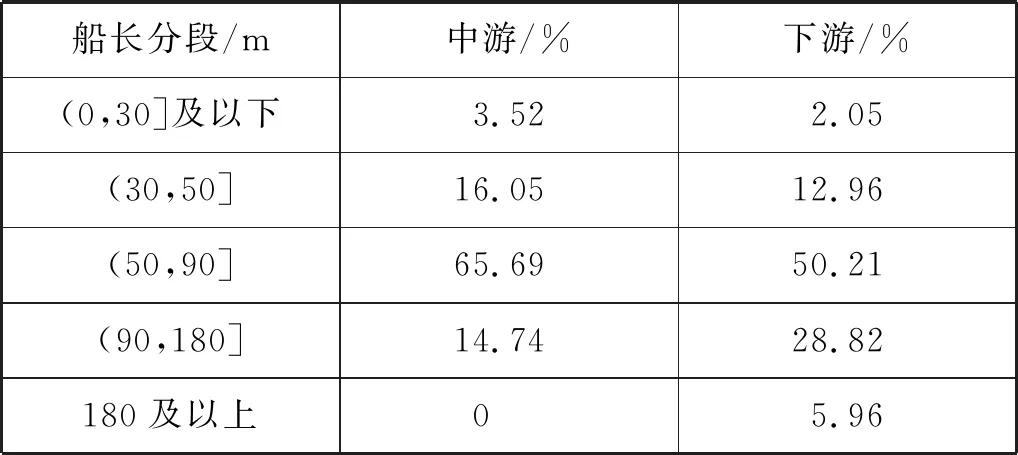
表8 长江中下游船舶长度分布

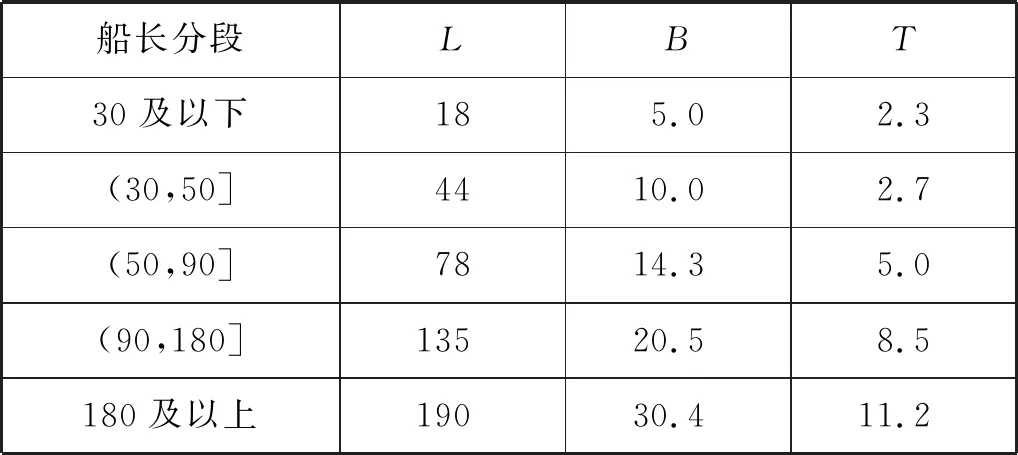
表9 代表船舶尺度 m

3.3.3碰撞角度

直角撞击一般会造成较大的后果，通常发生在横渡长江的客渡船、海事船和交通艇的碰撞中；其他沿江航行的货运、客运船舶在发生撞击时，以斜角撞击为主。内河船舶由于航道条件的限定，一般不会发生角度小于30°的撞击事故。因此，碰撞角度选择在30°～150°范围内随机产生，且撞击位置在艏部与艉部之间。

3.4 船舶吸能的计算和破损判定

碰撞吸能的计算基于外部动力分析，从动量守恒定理出发，通过解决碰撞过程中2艘船舶的刚体运动问题和船与水的耦合问题来估算碰撞能量。本文基于文献[2]提出的碰撞分析理论，通过碰撞能量解析表达式对被撞船吸收的能量进行估算。

根据第2.3节拟合得到的临界破损能量计算式进行破损判定，尚不足全面衡量船舶LNG储罐的安全性。不同船舶的LNG装载区长度有所不同，为体现这2种船舶的不同，引入系数k表征这种可能性为

(12)

式(12)中:LLNG为LNG罐箱或货罐在船长方向的长度;L为船长。

在进行LNG罐箱或货罐安全判定时，可利用lg(E/Ecr×k)作为判定标准，若该值大于0，则可认为LNG罐箱或货罐失效;若该值小于0，则可认为罐箱或货罐安全。

3.5 计算结果

根据上述方法，对LNG运输船和LNG罐箱运输船的LNG储罐破损概率进行计算，结果见图2～图9。

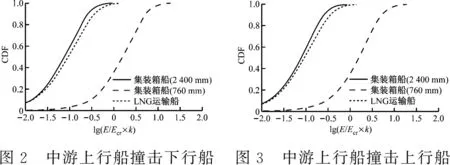
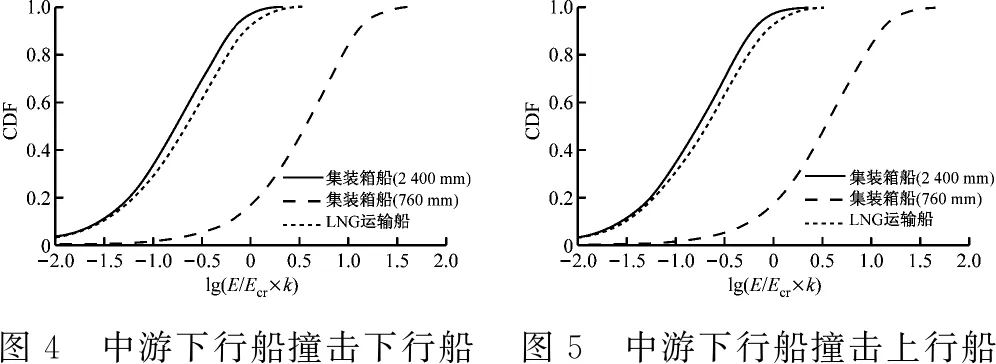
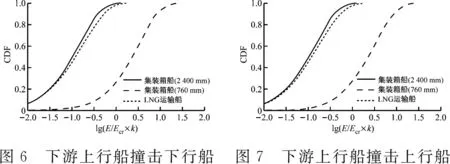
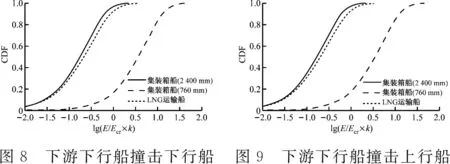
在按760 mm的要求进行LNG罐箱装载时，罐箱的平均破损概率约为76.18%，远高于LNG运输船的货罐破损概率4.81%，见表10。这说明在船舶碰撞事故发生时，现行试点阶段的装载要求不能有效防止LNG泄漏。当LNG罐箱按2 400 mm的要求装载时，罐箱的平均破损概率约为2.03%，甚至低于LNG运输船货罐的破损概率。

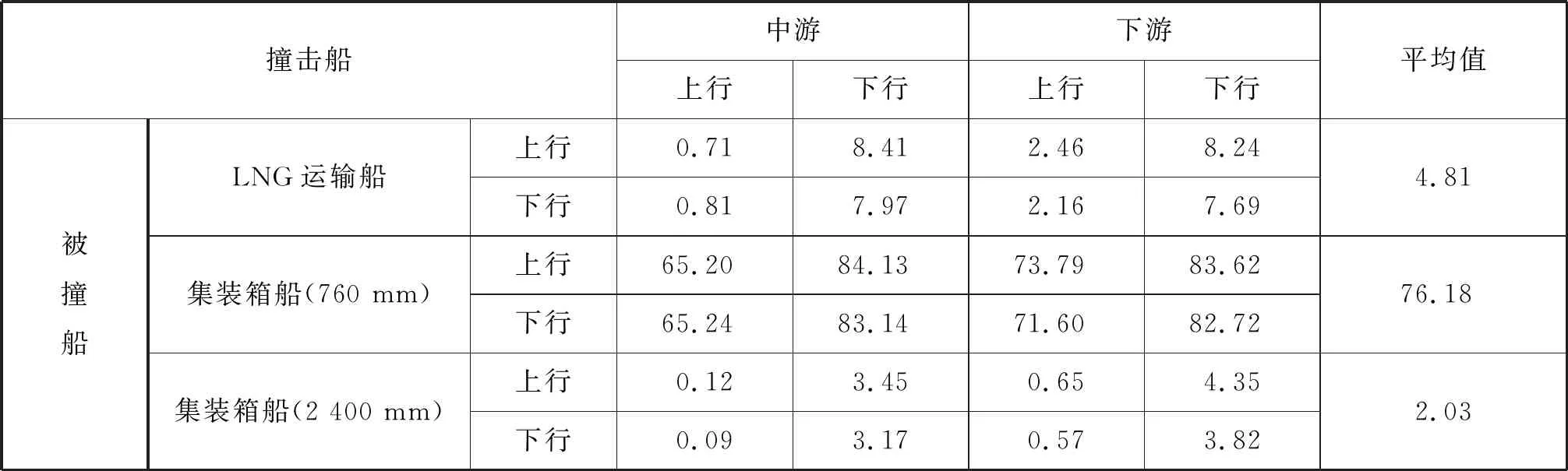
表10 LNG罐箱和货罐破损概率

4 结束语

通过船舶碰撞有限元模拟和蒙特卡洛计算，得到LNG运输船和罐箱运输船储罐临界破裂能量计算式和储罐破损概率。通过对计算结果进行分析，主要得到以下结论：

1) LNG罐箱在距离舷侧760 mm进行装载时，在碰撞中发生破损的概率约为76.18%，说明按现行的罐箱装载要求不能有效保证船舶碰撞中罐箱的安全性。若将罐箱与舷侧的距离增加至2 400 mm(即1个箱位)，船舶碰撞中罐箱的破损概率可降至2.03%，与C型舱LNG运输船的储罐破损概率4.81%相近。

2) 船舶航速对LNG储罐破损概率有直接的影响，长江下游船舶航速比中游船舶航速大，下行船的航速也要高于上行船。因此，长江下游LNG罐箱的破损概率要高于中游；当船舶受到下行船的撞击时，罐箱的破损概率要高于船舶遭受上行船撞击时的破损概率。