基于鲁棒自适应扰动观测器的船舶航向保持控制器设计

李纪强, 张国庆, 尚洪达

(大连海事大学 航海学院, 辽宁 大连 116026)

船舶航向保持控制研究一直是船舶海洋工程领域的一项重要课题，近年来，经典比例-积分-微分(Proportional Integral Differential,PID)控制、自适应控制技术、神经网络技术和智能控制技术等先进的控制技术不断被应用到船舶航向保持控制器设计中。[1-2]马超等[3]设计一种指数函数非线性反馈控制器，即在PID控制器中加入一项非线性的指数函数，达到调节船舶非线性的作用，并以“育鲲”轮为船舶模型进行仿真，验证其控制效果较好。由于欠驱动水面船舶的非线性特性，出现Backstepping方法与李雅普诺夫稳定性理论相结合的航向保持控制算法，文献[4]采用Backstepping方法直接将船舶非线性项设计到控制器中，但未解决Backstepping 控制器设计过程中计算负载大的问题。文献[5]采用动态面控制算法，解决虚拟控制律积分复杂且难以获得的难题，极大的降低Backstepping 控制器设计过程中的计算负载。然而，这些研究中均属于船舶航向保持算法，并且对于风、浪、流等外界海洋环境干扰通常以二阶白噪声或者是正余弦函数叠加进行代替[3]，由于白噪声具有很强的随机性，在上述控制器设计中，仅将此类扰动作为控制器的外界扰动，这对航向保持控制精度具有一定的影响。但在船舶路径跟踪领域，为提高船舶路径跟踪的控制精度，对于海洋环境干扰方面进行较深入的研究，除类似航向保持控制算法中以二阶白噪声代替外界环境摄动外，将海洋环境干扰近似为一类正余弦波也是一种被学者广泛接受的处理方法[6-8]，主要的研究方法有扩张观测器、扰动观测器和自抗扰控制等先进的控制算法[9-10]，文献[11]采用神经网络技术和最小参数化学习方法设计一种自适应扰动观测器，直接对控制系统进行补偿，提高控制系统的抗扰行和鲁棒性。张晓玲等[12]设计一种基于扰动观测的船舶轨迹跟踪自适应滑模控制算法，构造一种带修正泄漏项的自适应律来估计扰动观测的界，以提高控制器的抗扰性能和控制精度，仿真结果验证其具有较好的控制效果。为进一步补偿外界扰动，文献[13]和文献[14]将外界扰动作为一类补偿项，对系统控制器进行前馈定向补偿，但存在观测上界的限制，对外界环境扰动的自适应能力不足的缺点。

基于以上分析，本文采用非线性二阶Nomoto模型作为控制对象，在考虑外界海洋环境干扰的基础上，设计一种基于鲁棒扰动自适应观测器，并对船舶航向保持器进行反馈补偿，为直观表达本文的设计思路，系统信号流图见图1。本文的主要创新点为：在非线性Nomoto模型中，引入外界环境产生的扰动项，通过构造鲁棒自适应扰动观测器估计外界扰动项，并对航向保持控制器进行前馈补偿；通过结合动态面技术解决控制器设计过程中产生的“计算爆炸”问题，并利用Backstepping技术，设计基于鲁棒自适应扰动观测器的航向保持控制器，本文所设计的控制律具有形式简捷，控制精度高的优势。通过Lyapunov 稳定性判据证明所设计控制器的稳定性，并通过MATLAB仿真验证所设计的控制算法的有效性。

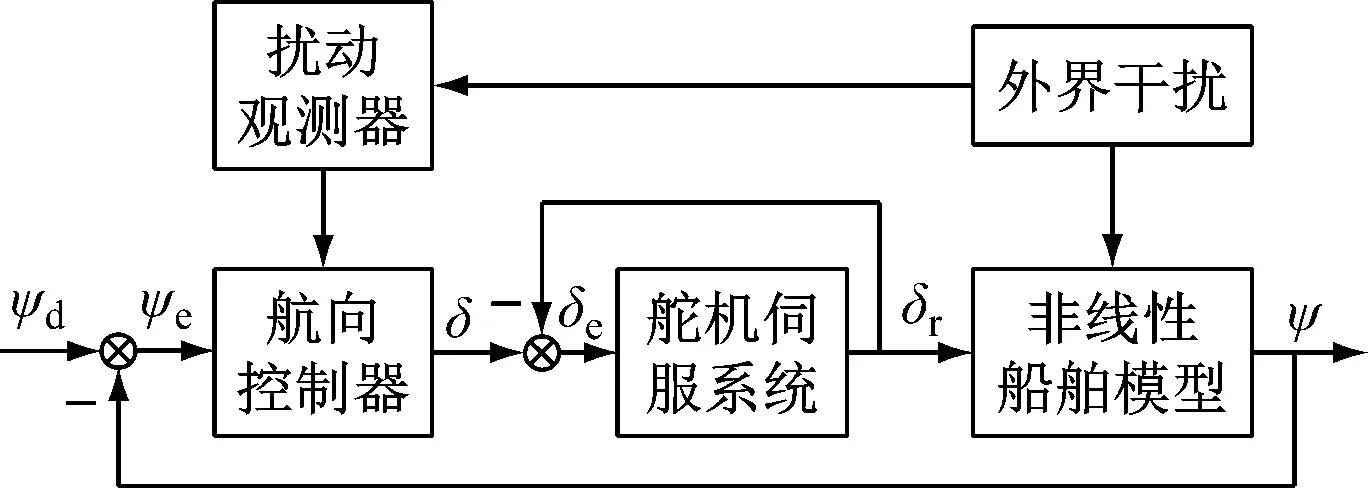
图1 船舶航向保持控制系统信号流图

1 模型描述

在船舶航向保持控制算法设计时，船舶数学模型常采用野本谦作提出的Nomoto模型，由于Nomoto模型适用于低频舵动和小舵角情况，存在一定的局限性。为消除这类局限性，船舶航向保持控制系统采用考虑外界海洋环境干扰的Nomoto非线性数学模型。

(1)

式(1)中:Ψ为航向角;δ为命令舵角;K和T为操纵性指数；dwr为外界扰动，为控制器设计需要，将式(1)写成状态方程的形式为

(2)

2 控制器设计与稳定性分析

2.1 控制器设计

对于非线性数学模型式(2)，利用Backstepping方法与动态面控制技术，设计基于鲁棒扰动自适应观测器的船舶航向保持控制算法。为增加控制器设计过程的严谨性，有如下假设：

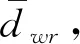
假设2：忽略海流对舵的影响，即不考虑海流影响。

控制器设计过程如下：

1) 定义误差变量，并对其时间求导得

Ψe=Ψ-Ψd

(3)

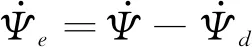
(4)

为镇定误差变量式(3)，设计虚拟控制律αr为

(5)

式(5)中:k1>0为设计参数，为避免在第二步中对αr求导造成的“计算爆炸”问题，采用动态面控制技术，令αr通过时间常数为τr的一阶滤波器βr，即

(6)

定义动态面误差变量qr=βr-αr，其微分表达式为

(7)

2) 定义误差变量re并对其求导为

re=αr-r

(8)

(9)

对外界海洋环境扰动dwr设计扰动观测器

(10)

(11)

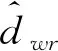
定义中间控制变量

(12)

设计中间控制变量u为

(13)

将式(12)代入式(13)得到控制律为

(14)

式(14)中：a1、a2和k2为设计参数。

2.2 稳定性分析

对于一般船舶控制系统，应用本文所提出的航向保持控制律式(14)和扰动观测器观测律式(10)和自适应律式(11)构建闭环控制系统。对于初始状态满足式的情况

(15)

通过适当的调节控制器设计参数k1、k2、Γ-1、τr、n1、n2、n3、σ、a1和a2，能够保证整个闭环控制系统的所有变量满足半全局一致最终有界稳定(Semi-Global Uniform and Ultimately Bounded, SGUUB)。

证明：选取Lyapunov候选函数

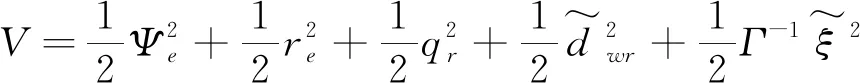
(16)

对其求导得

(17)

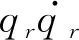
(18)

(19)

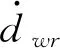
(20)

式(20)可写为

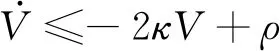
(21)

对式(21)积分，可进一步得到

V(t)≤ρ/2κ+(V(0)-ρ/2κ)exp(-2κt)

(22)

3 仿真试验

为验证本文所设计的基于鲁棒自适应扰动观测器的航向保持控制算法的有效性，本部分基于MATLAB仿真平台进行仿真对比试验，在模拟海洋环境下以“育鲲”轮的分离型数学模型[15]为控制对象进行仿真试验，由于在实际船舶控制工程中，执行器伺服系统的动态响应过程对控制系统的控制性能具有一定的影响，本文采用舵机伺服系统模型见图2，通过幅值饱和、速率饱和对执行器进行约束。“育鲲”轮部分参数和舵机伺服系统参数分别见表1和表2，“育鲲”轮分离型数学模型参数见文献[15]。海洋环境设为一般海况(4级)，风速Uwind=9.8 m/s，风向Ψwind=0°；海浪由传统PM谱产生。[16]船舶初始状态设置为

[x(0),y(0),v(0),Ψ(0),r(0),δ(0)]=

[0 m,0 m,0.5 m/s,-30°,0°/s,0°]

(23)

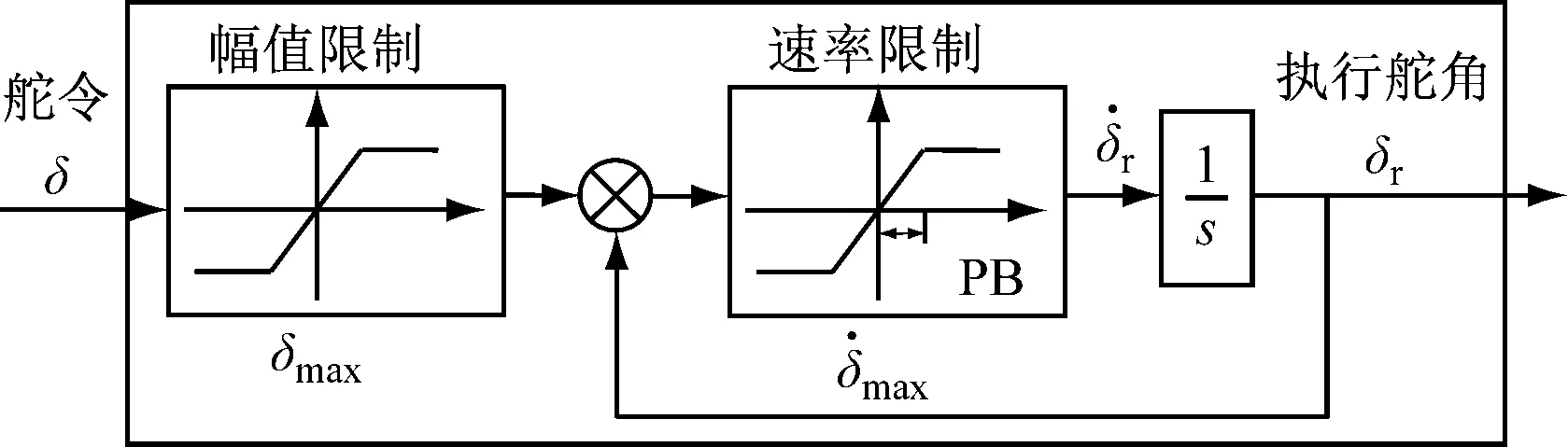
图2 舵机伺服系统模型框图

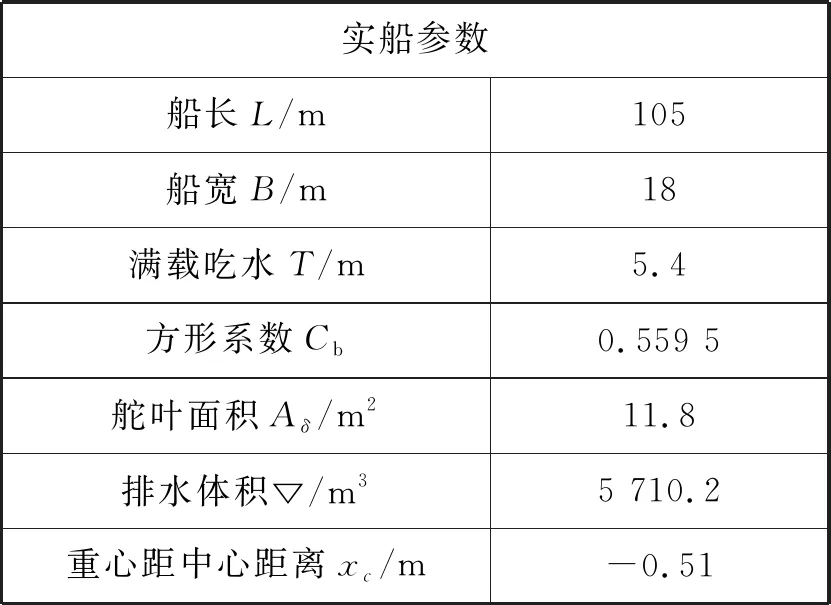
表1 “育鲲”轮相关参数

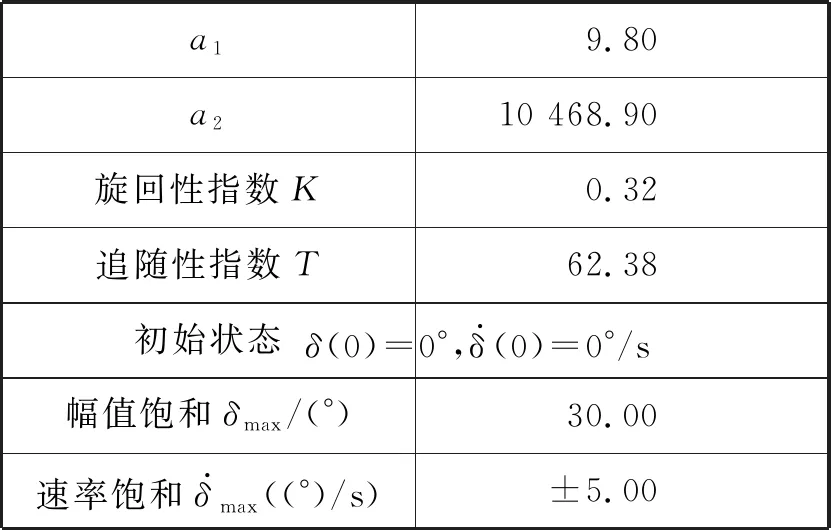
表2 数学模型和舵机伺服系统模型参数

仿真参数设置见式(24)，描述模拟海洋环境风场和波浪图见图3；在海洋环境干扰下的控制输出结果见图4；在海洋环境干扰下控制输入随时间变化曲线见图5；环境扰动和环境扰动估计值随时间的变化曲线见图6，扰动观测器的自适应参数变化曲线见图7。

k1=0.50,k2=1.20,Γ-1=0.10,σ=1.25,τr=0.20,n1=0.30,n2=0.70,n3=1.50

(24)

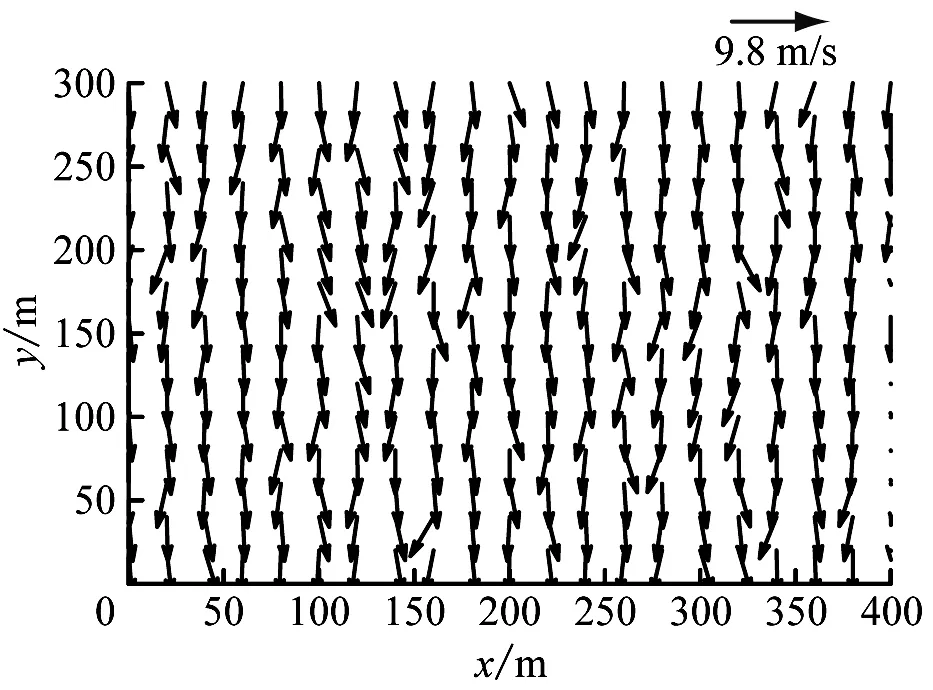
a) 2维风场图

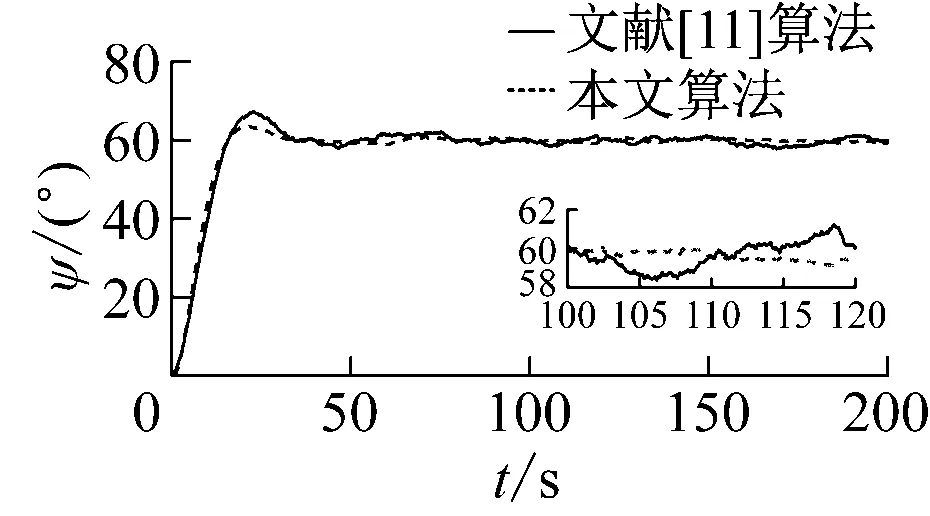
图4 控制输出曲线

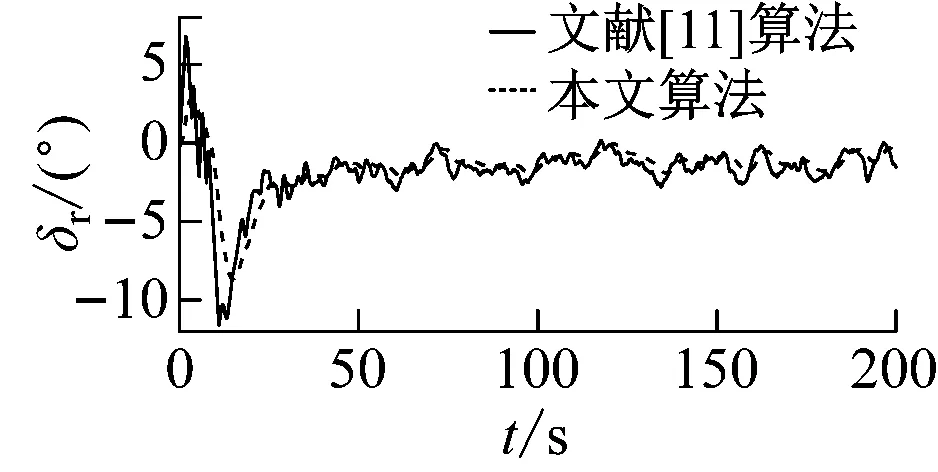
图5 控制输入曲线

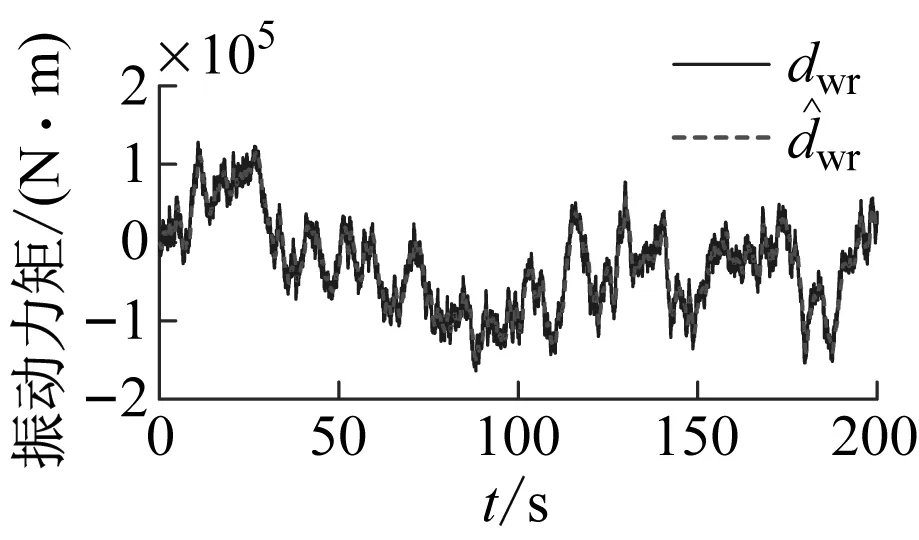
图6 环境扰动和扰动估计值

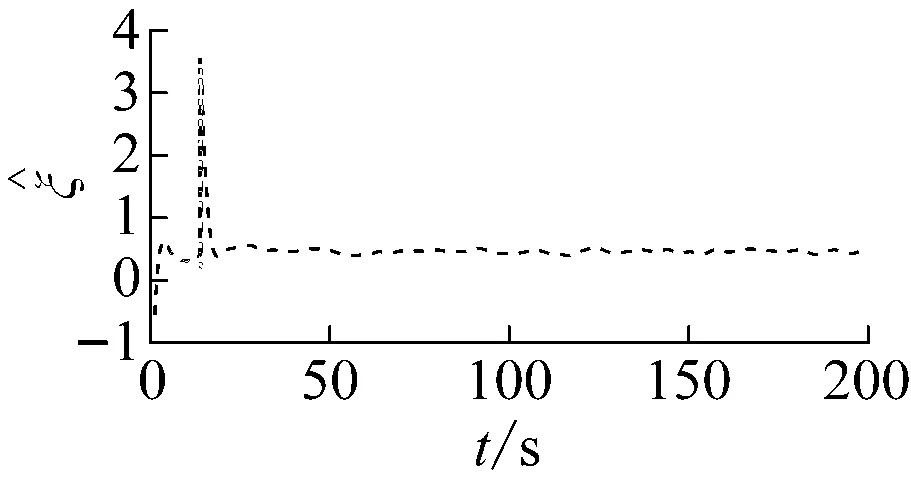
图7 环境扰动的自适应参数

对于外界海洋环境，本文基于挪威石油工业组织规范(Norsk Sokkels Konkurranseposisjon, NORSOK)构建风速风向模型，基于联合北海波浪计划(Joint North Sea Wave Project, JONSWAP)构建波浪模型来模拟外界海洋环境[16]，本文在7级海况下进行欠驱动船舶航向保持控制，模拟二维风场及三维海面波浪如图3所示。设置仿真时间为200 s，由图4可知:在2种控制算法的控制下，控制系统达到稳定的调节时间约33 s，但在文献[11]的控制下，超调量为10%；在本文算法控制下，超调量为4%。在闭环控制系统达到稳定状态后，控制输出信号在本文控制算法的控制下更加平稳，增加船舶航行的安全性与舒适度。由图5可知：为保证船舶航向稳定在60°，在文献[11]控制算法下的操舵频率高于本文控制算法，对舵机损耗较大。从对外界海洋环境的观测来看如图6所示，本文所设计的鲁棒自适应扰动观测器能够很好的外界海洋环境进行观测，并且在航向保持控制器中对外界海洋环境进行在线补偿，由图4和图5可知：闭环控制系统在在达到稳定状态后，鲁棒自适应扰动观测器能够有益地提高控制性能与控制系统的鲁棒性。

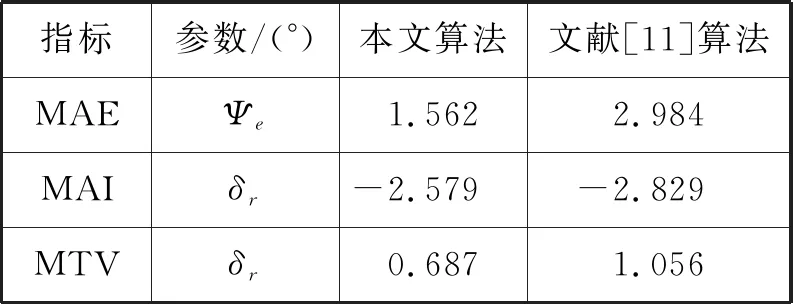
为进一步定量分析控制效果，选取性能指标函数式(22)来对比分析基于鲁棒自适应扰动观测器的航向保持控制算法与现有文献[11]中控制算法，输出误差绝对值平均值(Mean Absolute Error,MAE)，衡量系统输出响应频率；控制输入绝对值(Mean Absolute Control Input, MAI)，衡量系统控制输入平均值；控制输入平均变化绝对值(Mean Total Variation, MTV)，衡量能量消耗和曲线平滑度。控制性能定量对比见表3。由表3可知：在本文算法控制下，航向平均误差为1.562，优于文献[11]的控制算法；由于外界海洋环境的干扰作用，在控制系统达到稳定后，2种控制算法均需保持一定的左舵舵角来抵消环境干扰产生的转船力矩。由MTV可知：本文控制算法中舵机操舵频率明显下降，舵机损耗较低，能量消耗较低且舵机响应曲线较为平滑。相比之下，本文控制算法更具有工程实用性。

(25)

4 结束语

在实际海洋工程中，船舶航行不可避免地受到海洋环境扰动的影响，本文设计的基于鲁棒自适应扰动观测器能够较好地观测外界海洋环境，对航向保持控制器进行外界海洋环境干扰在线补偿，能够很好的减小外界干扰造成的控制器摄动，应用Lyapunov稳定性理论证明该控制器闭环系统内所有信号满足SGUUB。最后，以“育鲲”轮的分离型数学模型为控制对象，对所设计的基于鲁棒自适应扰动观测器的航向保持控制算法进行MATLAB仿真试验，并与现有文献[11]中的控制算法进行仿真对比试验，验证所设计控制算法的有效性和鲁棒性。