基于加权朴素贝叶斯的船舶轨迹分类算法
王维刚, 初秀民, 蒋仲廉, 刘 磊
(1.武汉理工大学 a.智能交通系统研究中心; b.能源与动力工程学院;c.国家水运安全工程技术研究中心,武汉 430063; 2.东南大学 交通学院,南京 211189)
随着我国经济的不断发展,内河水运日益繁忙,船舶交通流量越来越大,通航饱和度逐渐升高,航道通过能力趋于饱和,内河通航水域海事安全监管面临的挑战越来越大。[1]船舶自动识别系统(Automatic Identification System,AIS)能为水路交通安全研究提供海量的基础数据,在不同的研究方向都有广泛的应用。[2]随着智能航运的发展,AIS等数据呈现出指数级的递增趋势,开展船舶轨迹分类算法研究,有助于提高数据处理效率,为航运大数据的信息融合和综合利用奠定基础。通过基于AIS的船舶轨迹快速分类,有助于开展船舶运动模式识别和航行风险分析等,从而推动水路运输和海事安全监管向智能化、信息化方向发展。[3]
在船舶轨迹分类研究方面:PAN等[4]提出一种基于AIS数据的轨迹聚类模型,采用该模型分析航线,实现在没有先验知识的情况下自动对具有轨迹特征的不同航运路线进行分类。LI等[5]结合轨迹映射和聚类方法探索从AIS中获取的大数据,提出一种改进的基于密度的噪声应用空间聚类(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)算法,采用该算法聚类空间点,从而获得最优聚类。彭祥文等[6]利用云计算并结合聚类算法对船舶历史数据进行轨迹聚类分析,构建船舶航行正常轨迹模型,相比传统算法,能提升聚类效率。刘磊等[7]对轨迹间的平均距离、航速距离和航向距离进行融合,提出船舶轨迹间综合距离的概念,结合K最邻近(K-Nearest Neighbor,KNN)分类器进行内河船舶轨迹分类,效果较好。牟军敏等[8]提出一种基于豪斯多夫距离的船舶轨迹快速自适应谱聚类算法,实现高效快速的聚类,可准确地提取通航水域的主要船舶航路。朱姣等[9]提出增量式算法改进DBSCAN算法,用以高效地计算不同船舶的行为模式,基于轨迹分析挖掘船舶行为模式。这些研究主要采用聚类算法,以提高算法的效率和准确率为目的进行研究。在实际条件下,船舶航路较为固定,因而存在一些可利用的先验信息,采用有监督的学习优化分类效果。朴素贝叶斯法是基于贝叶斯定理和特征条件独立假设的分类方法,是众多的分类模型中应用最广泛的分类模型之一[10],所需的估计参数较少,对缺失数据不太敏感,相对简单。魏照坤等[11]利用AIS提供的数据分析通航水域船舶信息的分布情况,根据其概率分布,采用朴素贝叶斯算法,从船舶航速、航向和距航道边界距离等3个方面构建船舶异常行为检测模型,实现高精度的船舶异常行为检测。AUNG等[12]使用贝叶斯分类器对车辆行为进行分类,以预测道路网络的流量。ZHEN等[13]使用朴素贝叶斯分类器对厦门湾和城三角水域的船舶运动进行分类,据此检测船舶异常行为,研究中未见基于朴素贝叶斯模型的AIS轨迹分类相关研究。
本文以船舶AIS历史数据为基础,提出一种基于朴素贝叶斯算法的船舶轨迹分类方法,针对AIS轨迹分类场景,提出一种船舶轨迹特征组合,并对分类器进行加权优化,以提高分类效果。首先,通过AIS数据预处理提取轨迹特征;其次,选取最优特征集合并训练分类器,实现AIS轨迹数据的自动分类;最后,以长江武汉河段为例,对轨迹分类算法的有效性进行验证。
1 朴素贝叶斯轨迹分类算法
1.1 朴素贝叶斯
假设Y为要预测的某一轨迹类,X是包含n个特征属性X1,X2,…,Xn的已知轨迹,需求出轨迹X属于Y类的概率p(Y|X),以对比出X属于哪个轨迹类的概率最大,进而进行分类。[14]贝叶斯定理为
p(Y|X)=p(X,Y)/p(X)=
p(X|Y)p(Y)/p(X)
(1)
式(1)中:p(Y)为先验概率;p(Y|X)为后验概率;p(X|Y)为类条件概率;p(X)为证据。
朴素贝叶斯在计算p(X|Y)时,假设特征属性相彼此独立,该假设大大减少了估计的参数数量,由该假设可得
p(X|Y)=p(X1,X2,…,Xn|Y)
=p(X1,X2,…,Xn-1|Xn,Y)p(Xn|Y)
=p(X1|Y)p(X2|Y) …p(Xn|Y)
(2)
式(2)表明需要一部分已知类别的轨迹数据来训练分类器,统计得到各类别下各轨迹特征属性的条件概率估计值p(Xi|Y)。根据上述假设,式(1)可写为
(3)
式(3)为朴素贝叶斯分类器的基本方程。因为P(X)对每个轨迹类别都是常量,可忽略,仅考虑分子部分即可,所以基于朴素贝叶斯的AIS轨迹分类算法可定义为
(4)
式(4)中:X为待分类轨迹;yj为类别变量;Xi为X的轨迹特征。对于任一条轨迹X={X1,X2,…,Xn},该分类算法选择使后验概率p(yj|X)最大的类别作为该轨迹的类。
基于朴素贝叶斯的AIS轨迹分类算法流程为
1) 对AIS数据进行清洗与分包,得到有效的船舶轨迹数据。
2) 根据轨迹包含的AIS数据为每条轨迹计算相应的特征数据,并对特征数据进行高斯拟合,得到在不同类下各特征的高斯概率分布。
3) 计算各轨迹特征属性的条件概率估计值p(Xi|Y)。
4) 使p(X|Yj)P(Yj)最大的类作为分类结果,见图1。
1.2 轨迹特征
AIS轨迹特征的提取主要分为初步选择特征和寻找最优特征子集2步。初步选择特征是指根据AIS轨迹的特点,初步选择一些能区分不同类别的特征。根据初步选择的特征集合不一定能得到性能最好的分类器,可能会因冗余的特征项使分类器的精度降低,因此需进一步筛选寻找最优特征子集。

图1 分类流程
1.2.1特征初步选择
AIS船台发送的报文中主要包含静态信息和动态信息。其中:静态信息包括水上移动通信业务标识码(Maritime Mobile Service Identiftion,MMSI)、船名、呼号和船舶尺寸等;动态信息包括经纬度坐标、协调世界时间(Coordinated Universal Time,UTC)、航迹向、速度、艏向和转向率等。[2]借助船舶MMSI和时间信息,可对AIS数据进行分包处理,获得船舶轨迹信息[15],1条轨迹由若干离散的AIS数据组成,见图2。

图2 AIS轨迹图示例
1.2.1.1 方向
本文采用平均航向、航向最大值和航向最小值作为船舶轨迹特征等来反映轨迹的方向。不同类的船舶轨迹对应的航向会有显著差异,尤其是内河上行和下行的船舶航向相差约180°。
1.2.1.2 线形
轨迹的线形是轨迹最直观的特征,主要体现在轨迹的曲直上。顺直的轨迹与曲折的轨迹的最大转向率差异明显;同时,弯曲的轨迹相比顺直的轨迹,其航向方差要大很多。因此,本文选用最大转向速率和航向方差作为轨迹特征,以区分不同的轨迹线形。
1.2.1.3 动态信息
不同的轨迹类代表不同的航路和不同的运动模式,不同航路的通航环境一般存在着差异,导致船舶在不同航路上航行时存在速度上的显著差异,比如上行船舶与下行船舶受水流速度的影响,在对地速度上存在显著差异。因此,选用平均速度、平均加速度和平均角速度作为轨迹特征。
对于1条包含若干AIS信息的船舶轨迹,对所有速度信息进行平均得到平均速度为
(5)
对所有航向信息进行平均得到平均航向,并求出最大航向值、最小航向值与航向值的方差为
Hmax=max{H1,H2,…,Hn}
(6)
Hmin=min{H1,H2,…,Hn}
(7)
(8)
(9)
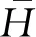
将所有AIS信息按时间排序,并将时间与航向差分得到前后两点的时间差和航向差,将航向差除以时间差得到转向率,可得到最大转向率和平均转向率为
(10)
(11)
(12)
同理,将速度差分可得加速度。
am=(vm+1-vm)/(tm+1-tm)
(13)
(14)
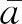
1.2.2序列前向选择算法
因船舶AIS轨迹的特征量较小,船舶轨迹分类算法采用一种启发式搜索方法,即序列前向选择算法。该算法适用于特征量较小的场合,是一种贪心算法。[16]以分类精度f为评价函数,Ωs为最优特征集合,Ω为所有特征集合,算法描述如下:
(1) 初始化Ωs为空集,则此时算法的分类精度fbest为占比最多的类的先验概率max{P(yj)}。
(2) 计算fmax=max{f(Ωs∪{F})},F∈(Ω-Ωs),F为某一特征。即选择一个在非最优特征集合中能得到最大精度的特征加入Ωs。
(3) 若fmax≥fbest,且Ω-Ωs≠∅,则令fbest=fmax转步骤(2),否则转步骤(4)。
(4) 得到最优特征子集Ωs,在Ωs上构建船舶轨迹分类器。
1.3 连续数据的处理与加权
在AIS轨迹分类算法中,需计算各轨迹特征属性的类条件概率估计值p(Xi|Y);AIS轨迹分类算法所选特征属性值均为连续值,不能直接估计出类条件概率。鉴于此,一般有2种处理方法:
1) 将连续值离散化[17],但该方法中离散区间划分的粒度控制难度较大,太细易导致某区间样本太少而不能可靠估计p(Xi|Y),太粗会使某些区间包含来自于不同类的样本,影响分类精度。
2) 假设连续变量服从某种概率分布,采用样本估计概率分布的参数,以类条件概率密度替代p(Xi|Y)。
本文采用第2种方法,结合高斯分布。对于每个类yi,属性xi的条件概率密度为
(15)
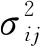
朴素贝叶斯分类器除了假设各特征相互独立以外,认为分类时各特征的重要程度相当;事实上,不同类别对不同特征的敏感性不同。为改进分类器的性能,可采用加权的方法[17-18],提出一种针对连续特征值的加权方法,对于任一条轨迹X={x1,x2,…,xn},其某个特征在类下服从正态分布N(uij,σij),则计算贝叶斯后验概率的每项P(Xi=xi|Y=yi),定义加权系数wij为
(16)
式(16)中:当σij较大时,表明在该类别下,特征值取值比较分散,反之表明取值较为集中。当特征取值集中时,表示对于类Yi,特征Xi具有较强的规律性,因此可提高其权重。
加权后的朴素贝叶斯轨迹分类器定义为
(17)
2 试验分析
2.1 试验数据集
以长江与汉江交汇河段为研究区域,开展船舶轨迹分类算法的验证研究。选取2017年5—7月的船舶AIS数据进行轨迹分类试验,试验原始数据中包含220多万条AIS数据。以5—6月份的数据训练分类器并测试准确率,以7月份的数据测试算法的分类效果。研究区域取左下角坐标(114.20 E,30.47 N)至右上角坐标(114.38 E,30.64 N)的矩形区域;分别定义长江航道上下游断面为A和B,汉江断面为C。因此,研究区域中存在船舶轨迹类1(A→B)、船舶轨迹类2(A→C)、船舶轨迹类3(B→A)、船舶轨迹类4(B→C)、船舶轨迹类5(C→A)和船舶轨迹类6(C→B)等6种类别轨迹。
经AIS数据经清洗和轨迹分离后,共得到7 095条船舶轨迹,其中5—6月份有4 826条,每条轨迹包含上百条到上千条AIS数据不等,通过绘图观察人工分类,构建原始数据集,分类结果见表1。
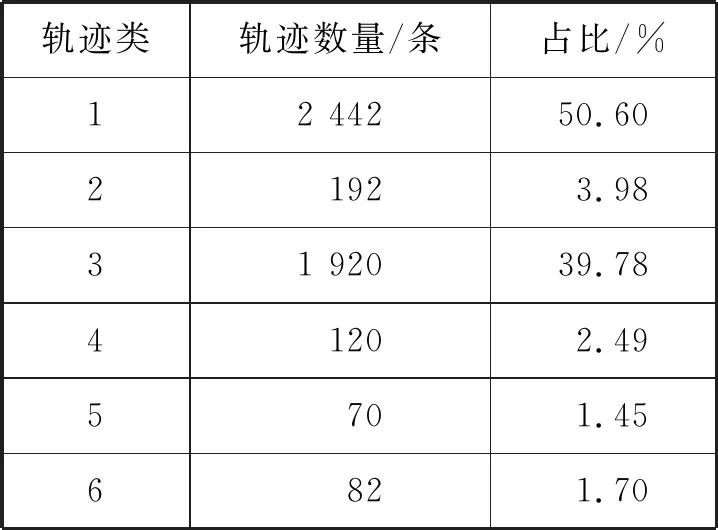
表1 人工轨迹分类
由表1可知:分布于长江主航道A与B之间的轨迹数量占绝大多数(约90.38%),去往汉江(支流)C截面的船舶轨迹相对较少,数据集的类别严重失衡。为减小算法的泛化误差、增强算法的泛化能力,采用欠采样的方式对数据集进行平衡。以轨迹类5为基准,在其余各类中随机采样70条轨迹,总共420条轨迹构成朴素贝叶斯轨迹分类模型的数据集。因训练集数量较少,为排除特殊情况,取10组平衡数据集计算结果的平均值作为最终结果。
试验时采用交叉验证的方式[19],将420条轨迹分层随机平均分为5组,每组各类别轨迹数量占比相当,依次以其中一组为测试集,其余4组为训练集进行模型的训练与测试,共5次。取每次的分类准确率的平均值作为整体的分类准确率,计算方法为
(18)
式(18)中:ACC为准确率;T为预测与实际相符的轨迹数量;E为预测与实际不相符的轨迹数量。
2.2 寻找最优特征子集
本文重点考虑8个轨迹特征,其编号为:
1) 平均速度;
2) 平均航向;
3) 平均加速度;
4) 平均转向率;
5) 最大转向率;
6) 航向方差;
7) 最大航向;
8) 最小航向。
按编号顺序累加观察算法的ACC变化,结果见表2。由表2可知:ACC不随特征的累积而稳定提升。例如:取前4个特征时的ACC相比取前3个特征有所降低,说明初步选取的特征存在冗余,会对ACC产生负面影响,需寻找最优特征子集,以提高算法分类ACC。

表2 特征累积下的模型准确率 %
采用序列向前算法寻找最优特征子集,经计算,依次向最优特征子集中添加特征2)、特征6)、特征7)、特征8)、特征1)和特征5),直至ACC达到99.05%;此后再添加,特征ACC不再提高。因此,最优特征子集包含平均航向、航向方差、最大航向、最小航向、平均速度和最大转向率,而平均加速度和平均角速度均为冗余特征。计算结果见表3。
2.3 特征加权
为揭示特征加权对轨迹分类效果的影响,对比分析加权前后的船舶轨迹分类算法的ACC。在研究过程中,将数据集分为平衡数据集和非平衡数据集(原始数据集),其结果对比见表4。
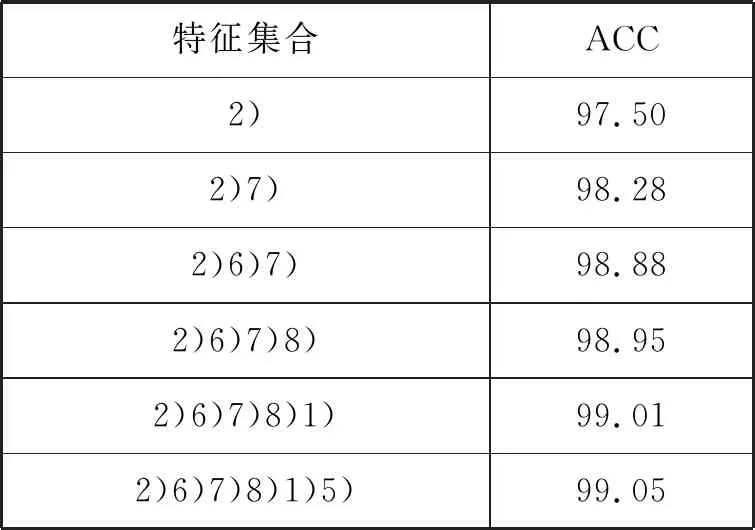
表3 寻找最优特征集合 %
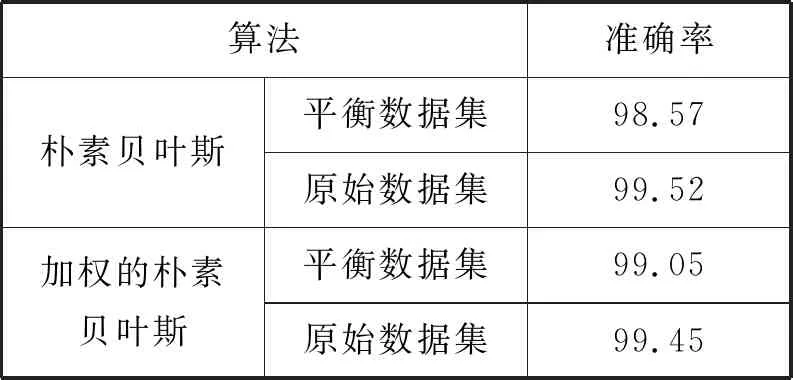
表4 加权前后结果对比 %
由表4可知:基于特征加权的AIS轨迹分类算法准确率较高,而非平衡数据集效果略差。上述结果表明,对于平衡数据集,本文建立的加权方法有助于提高算法的ACC。此外,平衡数据集的分类准确率整体低于非平衡数据集的原因在于数据量的差距;在非平衡数据集下,特征加权后ACC会相对下降的原因在于未加权时部分数据量占比小的类会被错误地分到数据量占比大的类中,特征加权放大相应特征对相应类别的影响,引起数据量较少的类的分类ACC提高,而数据量较大的类ACC相对减小,导致整体ACC有所下降。
3 分类效果与对比
为进一步测试算法对船舶轨迹的分类效果,采用训练好的分类器对研究区域7月份的船舶AIS数据进行分类。经数据清洗与轨迹分离之后,共得到2 274条待分类轨迹,采用加权的朴素贝叶斯轨迹分类算法对其进行分类,结果见图3。
除类2、类4和类6存在少许分类错误的轨迹,绝大部分船舶轨迹分类正确,分类效果良好,如表4所示。采用未加权的朴素贝叶斯轨迹分类算法进行分类,结果见图4。
由图4可知:类1、类3、类5和类6无明显错误,类4有少量错误,类2存在一定数量的分类错误。经验证,采用加权的船舶轨迹分类算法在新的样本上准确率约为98.96%,高于未加权算法结果(约98.24%),说明本文所建船舶轨迹分类算法具有良好的泛化能力。

a)类1(A到B)

a)类1(A到B)
本文采用相同的数据集,与其他常用分类算法进行对比分析;试验计算机条件为CPU i7-6700HQ 2.6 GHz、内存12 GB,对比各算法的分类准确率和处理速度,结果见表5。由表5可知:本文建立的改进朴素贝叶斯模型ACC最高,处理速度略低于未加权的朴素贝叶斯,相比其他方法优势明显。
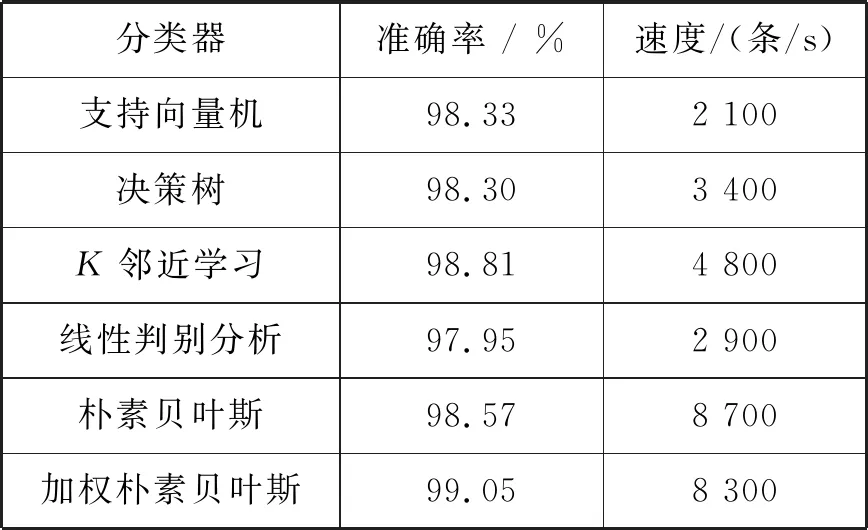
表5 不同分类器对比结果
4 结束语
本文针对内河船舶轨迹分类算法开展研究,提出一种特征为连续值时的加权方式,构建加权的朴素贝叶斯轨迹分类模型,提高船舶轨迹分类ACC。试验结果显示:船舶轨迹算法分类ACC不随特征数量的累积而单调递增;最优特征集合为轨迹平均速度、平均航向、航向方差、最大转向率、最大航向和最小航向;基于最优特征集合的分类算法ACC约为98.57%;基于最优特征集合的加权分类模型ACC约为99.05%;经加权的分类算法实际分类效果表现良好。
船速等运动特征可作为船舶轨迹分类的重要依据,基于朴素贝叶斯的船舶轨迹分类模型分类ACC达99%以上,可有效实现内河船舶轨迹分类,特征加权能有效提升算法分类的ACC和速度。该研究成果可为船舶异常轨迹识别、船舶航行风险分析等提供技术支撑。

