数学直觉思维的培养措施
张健

[摘 要] 逻辑推理是学好数学的关键,而直觉洞察却是实现数学创新必不可少的一种能力. 文章认为培养数学直觉思维的能力可以从以下四方面着手:关注数形结合,感悟直觉思维;利用大胆猜想,发现直觉思维;深化解题过程,形成直觉思维;强化辩证思考,升华直觉思维.
[关键词] 直觉思维;猜想;数形结合
数学家彭加勒曾经说过:“证明需要逻辑,而发明需要直觉. ”这句话形象地说明了直觉思维能力对学生创造意识的生成具有举足轻重的作用. 为了适应社会的发展对未来人才的需求,我们应从教学的各个环节上关注学生直觉思维能力的培养,笔者结合自身的执教经验,对直觉思维能力的培养措施提几点拙浅的看法,与君共勉.
关注数形结合,感悟直觉思维
数学本是研究现实生活中空间形式与数量关系的一门学科,将直观的形与可察的数结合在一起,就成了观察的真正内涵. 正如俗话所说:“善观者可见常人未见之事. ”引导学生在数形结合中善于观察与领悟,对直觉思维的发展具有重要意义. 布鲁纳认为教师使用直观的材料引导学生阐释直觉性的理解跟用演繹的方法证明同等重要. 数形结合则是用直观的形促进学生建立直观的心理感受,用直觉思维的发展带动逻辑思维的形成.
例1 已知,y=+,求y的最小值.
分析 不少学生看到此题有种无从下手的感觉,若结合图形进行分析,解题将变得容易很多. y=+代表点(x,0),(0,3),(8,1)之间的总距离. 如图1所示,在x轴到A点与到B点的距离之和.
根据图1可知,B点关于x轴对称的B′点坐标为(8,-1),y=+的最小值就是A点到B′点的距离. 所以y==4,因此,本题所求y的最小值是4.
观察坐标系图形中的动点三点之间的距离之和是解决此问题的关键,若光看题目,不使用直角坐标系进行解题,大部分学生都觉得束手无策. 一旦画出图形,此问题变得通俗、直观,学生解题将不再困难,这就是利用图形的直观性解决数学问题的基本方式.
教学中,不少教师和学生都偏爱以形助数的解题方式,的确,利用图形解决代数问题往往起到事半功倍的效果. 直觉观念的感悟与构建是培养学生直觉思维能力的基础,在教学中使用数形结合思想是促进学生观察与领悟数学事物变化规律的重要方式,学生在数形结合中促进直觉思维能力的形成与发展.
利用大胆猜想,发现直觉思维
大胆的猜想并非是毫无根据的主观判断,这里的猜想是指经过观察、操作、分析、类比与总结等各种数学思想转化后的一种思考. 利用大胆猜想,发现直觉是日常教学中常用的一种教学方法. 学生在教师的引导下,根据相应的数学现象充分发挥想象猜想相应的结论,这是培养学生创新能力必不可少的一个环节.
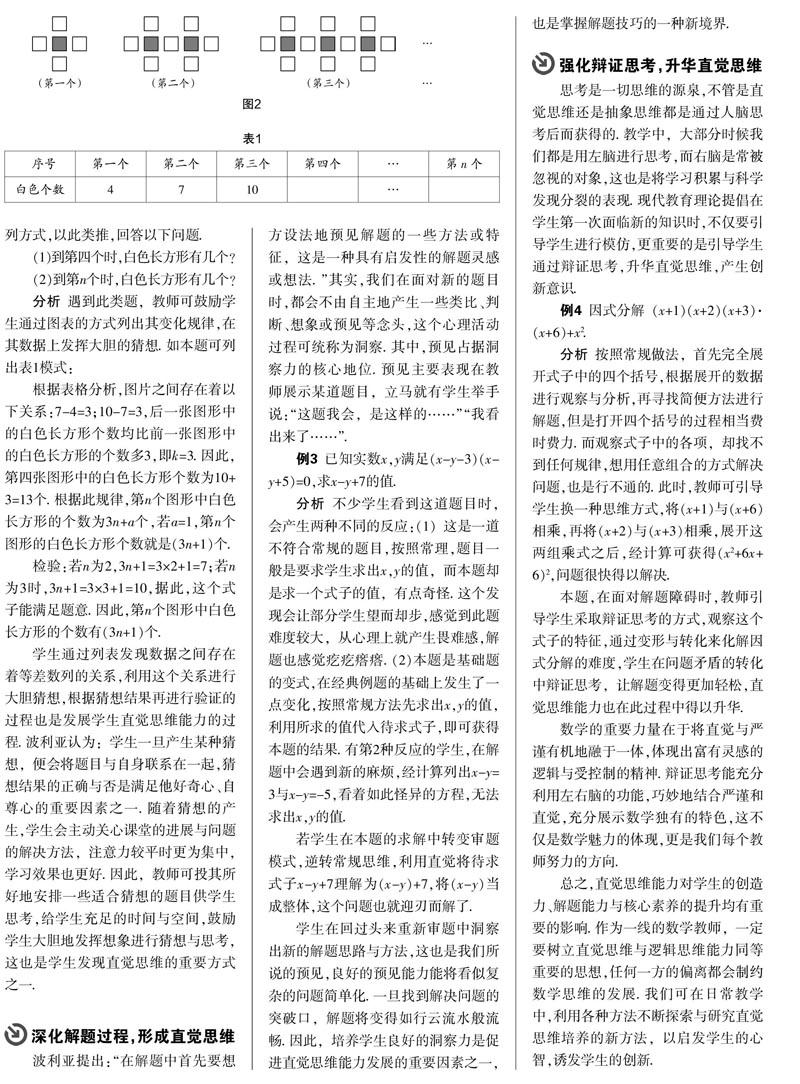
例2 观察下列黑白两种图形的排列方式,以此类推,回答以下问题.
(1)到第四个时,白色长方形有几个?
(2)到第n个时,白色长方形有几个?
分析 遇到此类题,教师可鼓励学生通过图表的方式列出其变化规律,在其数据上发挥大胆的猜想. 如本题可列出表1模式:
根据表格分析,图片之间存在着以下关系:7-4=3;10-7=3,后一张图形中的白色长方形个数均比前一张图形中的白色长方形的个数多3,即k=3. 因此,第四张图形中的白色长方形个数为10+3=13个. 根据此规律,第n个图形中白色长方形的个数为3n+a个,若a=1,第n个图形的白色长方形个数就是(3n+1)个.
检验:若n为2,3n+1=3×2+1=7;若n为3时,3n+1=3×3+1=10,据此,这个式子能满足题意. 因此,第n个图形中白色长方形的个数有(3n+1)个.
学生通过列表发现数据之间存在着等差数列的关系,利用这个关系进行大胆猜想,根据猜想结果再进行验证的过程也是发展学生直觉思维能力的过程. 波利亚认为:学生一旦产生某种猜想,便会将题目与自身联系在一起,猜想结果的正确与否是满足他好奇心、自尊心的重要因素之一. 随着猜想的产生,学生会主动关心课堂的进展与问题的解决方法,注意力较平时更为集中,学习效果也更好. 因此,教师可投其所好地安排一些适合猜想的题目供学生思考,给学生充足的时间与空间,鼓励学生大胆地发挥想象进行猜想与思考,这也是学生发现直觉思维的重要方式之一.
深化解题过程,形成直觉思维
波利亚提出:“在解题中首先要想方设法地预见解题的一些方法或特征,这是一种具有启发性的解题灵感或想法. ”其实,我们在面对新的题目时,都会不由自主地产生一些类比、判断、想象或预见等念头,这个心理活动过程可统称为洞察. 其中,预见占据洞察力的核心地位. 预见主要表现在教师展示某道题目,立马就有学生举手说:“这题我会,是这样的……”“我看出来了……”.
例3 已知实数x,y满足(x-y-3)(x-y+5)=0,求x-y+7的值.
分析 不少学生看到这道题目时,会产生两种不同的反应:(1)这是一道不符合常规的题目,按照常理,题目一般是要求学生求出x,y的值,而本题却是求一个式子的值,有点奇怪. 这个发现会让部分学生望而却步,感觉到此题难度较大,从心理上就产生畏难感,解题也感觉疙疙瘩瘩. (2)本题是基础题的变式,在经典例题的基础上发生了一点变化,按照常规方法先求出x,y的值,利用所求的值代入待求式子,即可获得本题的结果. 有第2种反应的学生,在解题中会遇到新的麻烦,经计算列出x-y=3与x-y=-5,看着如此怪异的方程,无法求出x,y的值.
若学生在本题的求解中转变审题模式,逆转常规思维,利用直觉将待求式子x-y+7理解为(x-y)+7,将(x-y)当成整体,这个问题也就迎刃而解了.
学生在回过头来重新审题中洞察出新的解题思路与方法,这也是我们所说的预见,良好的预见能力能将看似复杂的问题简单化. 一旦找到解决问题的突破口,解题将变得如行云流水般流畅. 因此,培养学生良好的洞察力是促进直觉思维能力发展的重要因素之一,也是掌握解题技巧的一种新境界.
强化辩证思考,升华直觉思维
思考是一切思维的源泉,不管是直觉思维还是抽象思维都是通过人脑思考后而获得的. 教学中,大部分时候我们都是用左脑进行思考,而右脑是常被忽视的对象,这也是将学习积累与科学发现分裂的表现. 现代教育理论提倡在学生第一次面临新的知识时,不仅要引导学生进行模仿,更重要的是引导学生通过辩证思考,升华直觉思维,产生创新意识.
例4 因式分解(x+1)(x+2)(x+3)·(x+6)+x2.
分析 按照常规做法,首先完全展开式子中的四个括号,根据展开的数据进行观察与分析,再寻找简便方法进行解题,但是打开四个括号的过程相当费时费力. 而观察式子中的各项,却找不到任何规律,想用任意组合的方式解决问题,也是行不通的. 此时,教师可引导学生换一种思维方式,将(x+1)与(x+6)相乘,再将(x+2)与(x+3)相乘,展开这两组乘式之后,经计算可获得(x2+6x+6)2,问题很快得以解决.
本题,在面对解题障碍时,教师引导学生采取辩证思考的方式,观察这个式子的特征,通过变形与转化来化解因式分解的难度,学生在问题矛盾的转化中辩证思考,让解题变得更加轻松,直觉思维能力也在此过程中得以升华.
数学的重要力量在于将直觉与严谨有机地融于一体,体现出富有灵感的逻辑与受控制的精神. 辩证思考能充分利用左右脑的功能,巧妙地结合严谨和直觉,充分展示数学独有的特色,这不仅是数学魅力的体现,更是我们每个教师努力的方向.
总之,直觉思维能力对学生的创造力、解题能力与核心素养的提升均有重要的影响. 作为一线的数学教师,一定要树立直觉思维与逻辑思维能力同等重要的思想,任何一方的偏离都会制约数学思维的发展. 我们可在日常教学中,利用各种方法不断探索与研究直觉思维培养的新方法,以启发学生的心智,诱发学生的创新.

