自动化铲板的对刀运动分析及其参数设计

丁彩红， 李署程， 吴喜如

(东华大学 机械工程学院， 上海 201620)

喷丝板是化纤纺丝生产的一个重要部件，由于纺丝溶液从喷丝孔挤出时的膨化胀大效应[1]，喷丝板使用一段时间后，在喷丝孔周围及喷丝板面上会积累一些结焦物，也可能有熔融细流黏结在喷丝板面，这些都会影响纺丝细流的质量[2]。为了保证化纤长丝的可纺性和质量稳定，须对喷丝板面进行定期铲板[3]。

目前主要采用人工铲板方式，工人举升铲刀压紧在喷丝板面进行铲板作业，由于举升速度过快，或者操作角度不合适，都可能划伤喷丝板面，甚至形成撞击坑点，影响纺丝质量。人工铲板质量严重依赖工人的熟练程度，并且工人劳动强度大，铲板质量不易控制，所以铲板自动化势在必行。目前德国欧瑞康纺织集团研发的铲板机器人的控制系统可与纺丝生产系统相互通信，使铲板时停泵时间更短，有利于提高纺丝稳定性，首台铲板机器人于2020年年初在印度的纺丝生产线上投入使用；国内有杭州锐冠科技有限公司研发的自动导引车(AGV)车载铲板机器人[4]和吴江朗科化纤有限公司研发的悬挂式喷丝板板面智能清理设备[5]在自动化铲板结构设计方面取得较好的成果。日本东丽株式会社则提出了不停泵纺丝的自动化铲板结构[6]。总体而言，国外技术的研究相对较早，但系统开发尚在起步阶段，市场化程度不高，且国外技术高度保密，鲜见于文献。自动化铲板技术主要体现在铲板结构设计、铲板运动规划和自动化铲板工艺等方面。本文针对铲板运动规划，提出对刀运动速度控制曲线规划，建立对刀运动的碰撞理论模型，开展了对刀运动参数的设计，为机械缓冲结构中弹簧刚度系数的计算提供技术参数。

1 铲板自动化系统设计

1.1 基于机器人的自动化铲板系统

应用AGV移动和机器人技术，设计自动化铲板系统，如图1所示。

图1 自动化铲板机器人系统Fig.1 Automatic scraper robot system

AGV小车在纺丝车间平行纺丝设备作移动导航，使机器人系统到达某个纺丝箱位置，通过机械或激光定位，使机器人末端移动到该纺丝箱的喷丝板下方。然后机器人举升末端执行器以快速上升—接近—接触的方式压紧在喷丝板面以产生一定的铲板接触力来进行刮铲作业，其中，末端执行器被举升完成铲刀和喷丝板面接触并压紧的过程称为对刀运动，铲刀进行刮铲作业称为刮铲运动。

1.2 铲板末端执行器的结构

由图1可知，末端执行器包括2组铲刀组件，可1次同时刮铲2个喷丝板面，2组铲刀组件由1个动力驱动通过同步带以等速旋转。铲刀组件的结构如图2所示，包含3个独立刀组，刀组上的3把铲刀以120°分布实现高效率的刮铲作业。每个刀组通过3个并联的底座弹簧K1和刀组底座连接，使刀组可在竖直方向被压缩以产生铲刀与喷丝板面之间的接触力，并在水平方向可摆动以适应铲刀刀刃平面与喷丝板面的不平行。由于机械装配很难保证使每个铲刀的刀刃和铲刀组件的水平面绝对平行，也很难保证3个铲刀形成的刀刃平面和喷丝板面绝对平行，为此设计铲刀与铲刀座的结构关系如图3所示。

图2 铲刀组件Fig.2 Scraper component

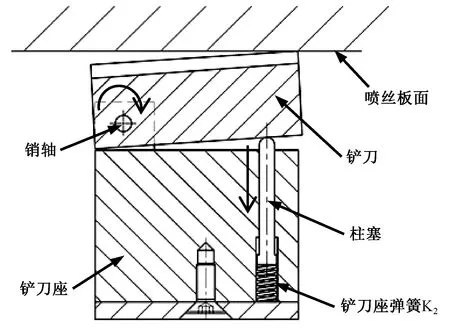
图3 铲刀与刀座的结构关系Fig.3 Structural relationship between scraper and holder

铲刀可绕铲刀座做微小转动，由于铲刀座弹簧K2的作用使铲刀在被举升过程中刀刃逐步接触并保持贴紧在喷丝板面，同时3个铲刀刀刃由于与喷丝板面的接触约束而成一个平面，保障了多铲刀同时刮铲的有效进行。

2 对刀运动的速度控制曲线设计

2.1 对刀运动过程描述

对刀运动的基本过程如图4所示。经历对刀前的就位、对刀碰撞瞬间、铲刀刀刃全部接触喷丝板面和完成对刀4个关键位置节点和时刻。

图4 对刀运动过程位置示意图Fig.4 Schematic diagram of position during tool setting movement

a) 对刀就位：t0时刻。机器人末端定位至喷丝板面正下方hm处。

b) 对刀碰撞：t1时刻。机器人末端举升，至铲刀刀刃抵触喷丝板面，机器人末端运动至位移X1。

c) 刀刃全接触喷丝板面：t2时刻。机器人末端继续举升，至铲刀刀刃完全接触喷丝板面，机器人末端运动至位移X2。

d) 对刀完成：tm时刻。机器人末端继续举升，底座弹簧继续被压缩，铲刀相对于喷丝板面保持静止，但铲刀和喷丝板面的接触力逐渐增大，直到达到所需铲板接触力。机器人末端运动至位移Xm。

2.2 对刀运动的速度控制曲线

在机器人末端执行器的对刀运动中，末端执行器在t0～t1阶段作匀速或匀加速运动，在t1时刻铲刀具有最大速度，定义为对刀阶段1；在t1～t2阶段作匀速或匀减速运动，在t2时刻铲刀的速度为零，与喷丝板面相对静止，定义为对刀阶段2；在t2～tm阶段作匀减速运动，在tm时刻末端执行器的速度为零，定义为对刀阶段3。

机器人末端执行器的加减速控制算法通常为梯形速度曲线控制、正弦加减速控制和S型速度曲线控制[7]。选取梯形速度曲线控制方式规划对刀运动，提出铲板末端执行器的对刀运动速度分布曲线的规划设计如图5所示。可看出，最大对刀运动速度(简写为最大对刀速度)vmax的确定是运动控制曲线规划的关键。自动化铲板作业时，末端铲刀组件的快速对刀使铲刀接近并接触喷丝板面时，不允许损伤喷丝板面或者铲刀刀刃，为此应用接触碰撞理论建立铲刀和喷丝板接触碰撞过程的数学模型，从而求得最大允许碰撞速度，即为最大对刀速度vmax。

图5 对刀运动的速度控制曲线Fig.5 Speed control curve of tool setting motion

3 铲刀和喷丝板面的接触建模

铲刀刀刃与喷丝板面的宏观线接触，实际上是由铲刀刀刃上的微凸体与喷丝板板面的微观点接触所组成，为此，以微凸体与理想刚性平面的接触为例[8]，如图6所示。从微观层面展开铲刀刀刃与喷丝板面的完全弹性变形和完全塑性变形的接触分析。其中：R为微凸体半径，ωe、ωp为微凸体法向变形量；Ne为弹性法向载荷、Np为微凸体与刚性平面接触时的法向载荷，下标e和p分别表示完全弹性状态和完全塑性状态。

图6 微凸体的完全弹性与塑性变形Fig.6 Elastic (a) and plastic (b) deformation of microconvex bodies

由经典Hertz理论可知完全弹性接触情况下微凸体法向接触变形与载荷、实际接触面之间的关系[9]为：

(1)

(2)

式中：E为等效弹性模量，E1为材料弹性模量，N/mm2；R为微凸体半径，mm；ωe为微凸体的弹性变形量，mm；ν1为材料泊松比；Se为弹性接触情况下微凸体实际接触面积，mm2。

(3)

式中：H为材料的硬度，N/mm2；Kc为最大接触压强系数，取值为

Kc=0.454+0.41ν1

令ω′p为微凸体的临界塑性变形量，超过该临界值，可认为微凸体进入完全塑性变形阶段，其取值[11]定义为

ω′p=110ω′e

(4)

由Abbott理论可知，完全塑性变形下的法向接触采用线性硬度模型表示[12]，微凸体所受法向载荷Np和法向变形量ωp的关系为

(5)

式中，Sp为塑性接触情况下微凸体实际接触面面积，mm2。

由于铲刀加工、修磨存在误差等原因，经多次实物测量得铲刀刀刃曲率半径r1∈[0.2,0.5]mm，已知铲刀与喷丝板的基本参数如表1所示。

表1 铲刀与喷丝板的基本参数Tab.1 Basic parameters of scraper and spinneret

将曲率半径r1和表1中铲刀的参数代入式(3)和(4)，可求得临界弹性变形量ωe为1.78×10-5～4.45×10-5mm，ωp为1.96×10-3～4.89×10-3mm。当铲刀刀刃发生完全塑性变形且变形量达到0.1 mm时，由式(5)可算得此时铲刀刀刃所受接触载荷Np为129.31～323.27 N，对应的塑性变形时接触区面积Sp为0.125～ 0.314 mm2。

喷丝板表面粗糙度值为0.2 μm，当单个微凸体发生完全塑性变形的变形量达到0.2 μm时可认定喷丝板发生损伤，由式(5)求得作用于喷丝板面单个微凸体的法向载荷Np为8.62×10-4N，在接触面积为Sp的接触区内，含有约0.5×106～1.25×106个高度和半径为0.2 μm的喷丝板面微凸体，则喷丝板表面发生损伤需要的接触力约为431.0～1 077.6 N，而在同样的接触面积，使铲刀刀刃受损的接触力仅为约129.31～323.27 N。

上述分析说明铲刀刀刃和喷丝板面接触碰撞时，铲刀刀刃远比喷丝板面容易受损，因此，确定铲刀快速对刀时以铲刀刀刃不受损为对刀运动的规划原则，

后续将开展铲刀刀刃和喷丝板面的碰撞分析，从而求得铲刀在接触碰撞喷丝板面瞬间的最大允许速度。

4 铲刀和喷丝板面的碰撞分析

4.1 铲刀和喷丝板面的接触碰撞力

对刀时铲刀与喷丝板的接触碰撞过程如图7所示。二者碰撞前的瞬间速度分别为v10、v20，喷丝板为静止，故v20等于0 mm/s，铲刀碰撞接触点的曲率半径为r1。通过对手工铲板的操作规范以及铲板时铲刀和喷丝板面的磨损、局部损坏形成的点坑状面积形态的观察发现，对刀时铲刀和喷丝板面的接触碰撞属于低速碰撞，且碰撞过程连续，接触形态为点与点的小变形碰撞。因此，应用Hertz接触理论[13]将铲刀和喷丝板面的碰撞接触简化为弹簧阻尼系统，碰撞过程分为压缩与弹性恢复阶段，且弹性碰撞发生在一个局部的接触区域内。

图7 铲刀与喷丝板面的接触形态Fig.7 Contact form between scraper and spinneret surface

由广义Hertz公式，物体碰撞力[14]有如下形式：

(6)

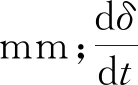
(7)

式中：E1和E2为铲刀与喷丝板的弹性模量，N/mm2；ν1和ν2为它们的泊松比，此时等效曲率半径r=r1。

由Hunt假设[15]可知，铲刀和喷丝板在碰撞期间的能量被阻尼耗散，碰撞期间的能量损失等于图8所示滞后环积分所得的能量损失。

图8 Hertz接触力滞后环曲线Fig.8 Curve of Hertz contact force lag

于是得到滞后阻尼系数λ和恢复系数e之间的关系为

(8)

将式(8)代入式(6)，化简得到碰撞力

(9)

4.2 最大压入变形量和最大碰撞力

(10)

当物体碰撞速度已知，则最大压入变形量和碰撞接触时间可确定，则压缩阶段的运动方程为

(11)

对式(11)进行一次积分运算并代入压缩开始和结束时碰撞速度的已知条件，可求得最大压入变形量为

(12)

由式(12)可知，两物体碰撞时的最大压入变形量与物体质量、材料性质、赫兹刚度以及碰撞前的速度有关。

4.3 碰撞时间

对式(11)进行积分后，经过算式变化可得：

(13)

令x=δ/δm，对上式积分可得：

(14)

当δ=δm，即x=1时，有：

(15)

假定如图8所示的加载(压缩)段和卸载(恢复)段所用时间相等，则由式(14)和(15)可得碰撞过程的总时间

(16)

综上所述，通过对两物体正面碰撞展开理论分析，得到铲刀与喷丝板面的碰撞过程中碰撞力、碰撞变形、碰撞时间与碰撞速度之间的数学表达关系式，为后续开展对刀运动中铲刀最大对刀速度的分析计算提供设计依据。

5 对刀运动的最大对刀速度设计

由铲刀和喷丝板面的接触建模可知，碰撞接触时铲刀刀刃远比喷丝板面容易变形，为此，将碰撞过程的压入变形量全部折合作用在铲刀刀刃上来进行后续的分析。

依据对铲刀和喷丝板接触碰撞过程的分析，应用MatLab分析软件开展刀刃曲率半径为r1的铲刀以不同的速度v10与喷丝板面接触碰撞的计算分析，得到最大压入变形、最大碰撞力、碰撞时间与碰撞速度v10的关系，如图9所示。

图9 铲刀与喷丝板碰撞过程相关参数的关系分析Fig.9 Analysis on relationship of parameters in collision between scraper and spinneret. (a) Maximum press-in deformation and collision speed; (b) Maximum collision force and collision speed;(c) Collision time and collision speed

由图9可知最大压入变形量和最大碰撞力随碰撞速度的增大而增大，碰撞时间随碰撞速度的增大而缩短，且碰撞总时间均非常小，可不予考虑；在相同的碰撞速度下，曲率半径越小越不利于碰撞。以刀刃曲率半径0.2 mm的铲刀为例，设定最大允许损伤为0.1 mm(即最大压入变形量δm为0.1 mm)为对刀运动参数的规划条件，铲刀的最大对刀速度vm为87.07 mm/s，对应的最大碰撞力Fm为1 643.75 N，铲刀与喷丝板的碰撞时间Δt为3.47×10-3s。

通常，以一定的安全冗余设计对刀运动中铲刀的对刀速度v′m

v′m=vm/κ

(17)

取安全系数κ为1.5，可求得铲刀对刀速度v′m为58 mm/s。由图9(b)可查得曲率半径0.2 mm的铲刀刀刃在该速度下受到的碰撞力Fm约为840.46 N。

6 结 论

自动化铲板作业中铲刀快速接近并压紧在喷丝板面的对刀运动不允许对铲刀刀刃或者喷丝板面造成损伤，为此开展了对刀运动的运动过程分析和运动参数设计，得到以下结论：1)应用Hertz接触理论建立对刀运动中铲刀和喷丝板面的接触模型，分析得到在对刀时铲刀刀刃远比喷丝板面容易受损，因此确定以不损伤铲刀刀刃为对刀运动参数的设计原则；2)应用广义Hertz公式和碰撞能量损失模型，推导得出铲刀和喷丝板接触碰撞时的最大碰撞力、最大压入变形量及碰撞时间与碰撞速度之间的数学关系式；3)应用MatLab计算分析，发现最大压入变形量和最大碰撞力随碰撞速度的增大而增大，且碰撞时间非常短，在相同的碰撞速度下，铲刀刀刃的曲率半径越小越不利于碰撞；4)针对一个刀刃曲率半径为0.2 mm的铲刀，设定最大允许损伤为0.1 mm，得出对刀运动的最大对刀速度为87.07 mm/s，取安全系数为1.5时的对刀速度为58 mm/s，碰撞力约为840.46 N。这为后续开展铲刀组件结构的详细设计提供了依据，尤其为机械缓冲结构中弹簧刚度系数的计算提供了必要的技术参数。