针对凸多面体组合结构的二重迭代浮态计算方法

刘虓 徐磊 樊天慧 陈超核

(华南理工大学 土木与交通学院，广东 广州 510640)

随着世界各国尤其是涉海国家正在积极实施海洋战略，以浮式海洋平台为代表的各种超常规外形的水面浮体不断涌现。这些浮体的结构形式与常见的水面浮体——单体船的最大区别在于：前者由多个凸多面体组成，而后者只有一个凸多面体(忽略舵、桨及其它细小附体结构)。浮态是所有浮体性能的基础性指标。单体船[1- 2]的浮态研究已经成熟，其计算方法深刻影响了以多体船[3]和浮式海洋平台[4- 5]为代表的凸多面体组合结构的浮态计算。近年来随着计算技术的进步，浮态计算方法尤其是凸多面体组合结构的浮态计算出现了新的趋势和演变。

首先是计算模型的新趋势。浮体的研究对象从常规船舶过渡到多体船、海洋平台乃至超大型浮式平台等，浮体外形的描述方法由基于二维切面的常规船舶型值表，发展为三维“面元”[5- 6]模型乃至三维“体素”模型[7- 8]。建立三维面元模型的图形软件/格式/库有：CATIA软件[9]、STL图形格式[10]、CGAL几何算法库[11]、有限元软件PATRAN[12]等。三维“体素”模型[8]的提出基于“离散组合”的思想：将复杂形状的浮体分解为若干简单的“体素”(圆柱体、长方体、棱锥等)，首先求解各体素的排水体积、浮心坐标及水线面要素，然后进行组合得到整个浮体的浮态要素。四面体是最基本的体素单元，其它所有的体素均可分解为四面体。刘虓[7]据此提出了基于四面体的计算模型，陈彦璋[5]也利用四面体计算海洋平台的体积要素。但是他们并没有将基于四面体模型的方法与传统的基于二维切面模型的算法进行比较研究。

其次是计算方法的新趋势。浮态计算是一个反复迭代的过程，传统方法分为两类：矩阵迭代法和非线性优化算法。赵晓非[13]提出船舶浮态计算的矩阵迭代方法。该方法每次迭代需计算船舶水面要素(投影面积、漂心坐标、惯性矩)和水下体积要素(排水体积和浮心坐标)，比较繁琐。近期，学者们又倾向于将浮态问题归结于非线性优化问题，避免了水线面要素计算[14]。但是这些方法的收敛性存在问题：以Powell法和0.618法为代表的直接搜索法容易陷入局部最优解；以遗传算法为代表的现代启发式算法又不能保证每次计算都能收敛至最优解。

文中基于四面体网格模型提出了一种新型的双重迭代法，通过内、外双层迭代，分别模拟浮体的升沉和旋转运动，具有明确的物理意义。文中还通过实验证明了算法的可靠性、精度和良好的收敛性，并进一步通过数值实验比较了传统算法和文中算法在精度计算上的差异和产生原因。实验对照分析表明：文中方法比传统方法更适合分析“凸多面体”[13]组合结构的浮态问题。

1 预备知识

1.1 凸多面体、坐标系和包围盒

如果多面体在它们每一面所决定的平面的同一侧，则称此多面体为凸多面体[15]。图1所示的半潜式海洋平台即是由立柱、横箱、下浮体等多个“凸多面体”构成的组合结构。

图1 半潜式海洋平台

文中采用浮体坐标系xyz和地球/全局坐标系xGyGzG这两个右手坐标系来研究浮体平衡问题。包含浮体的最小长方体称为“包围盒”(如图2所示)。

图2 浮体坐标系xyz、全局坐标系xGyGzG和包围盒

1.2 浮态参数/水平面方程

文中假定浮体不动，其浮态体现为浮体坐标系下的水平面方程：

nx·(x-xp)+ny·(y-yp)+nz·(z-zp)=0

(1)

式中：水平面的法向量N为〈nx，ny，nz〉，面内某点p的坐标为(xp，yp，zp)。

平面方程一般表达式为：

Ax+By+Cz+D=0

(2)

对比式(1)、(2)，得：

(3)

1.3 浮体平衡条件

浮体平衡条件如下：

(Ⅰ)V=P/γ；

(Ⅱ)l(B，G，N)= 0。

式中，V为浮体排水体积，P为浮体重量，γ为水的重度，B为浮体浮心坐标，G为浮体重心坐标，N为水平面法向量(假设浮体固定，水面法向量可变)，l为浮力作用线与重力作用线的距离。

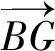
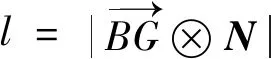
(4)

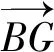
1.4 基于四面体网格的浮态计算

四面体(三棱锥)是最基本的三维体单元(如图3所示)。任何三维浮体均可分解为四面体单元(如图4所示)。文献[7]中提供了长方体、圆柱体、三棱柱分解为四面体的方法。

四面体体积为

图3 四面体单元

图4 利用FEM软件将船体分解为多个四面体单元示意图

(5)

四面体形心坐标为

(6)

式中，四面体(如图3所示)的顶点i坐标为(xi，yi，zi)，其中：i=A，B，C，D。

将三维浮体分解为多个四面体后，只要逐个计算每个四面体的排水量和浮心坐标，就可汇总得到整个浮体的排水量和浮心坐标。文献[7]中列举了四面体与水平面相对位置的5种可能情况(如图5所示)，并逐一进行了分析。

图5 四面体与水面的切割关系(共5种，此处仅列举2种)

2 双重迭代法求浮态

文中提出的浮态求解方法是一种迭代法，包含内、外两层迭代。

2.1 内层迭代(模拟升沉)

假设浮体只进行升沉运动(暂时约束其旋转运动)，可用内层迭代法来确定水平面方程。展开具体论述前，先观察图6所示的浮体包围盒，并令8个顶点距池底的距离为

hi=lxi+myi+nzi，i=1，2，…，8

(7)

式中：l、m、n为水平面法向N(图6中全局坐标系的zG轴指向)与浮体坐标系x、y、z轴夹角的余弦。

图6 浮体包围盒示意图

找出最小值h0及其对应顶点v0；最大值h1及其对应顶点v1。如图6所示，2号点为v0，距离池底的距离22’即为最小值h0，7号点为v1，距离池底的距离77’即为最大值h1。当水平面通过v0(2号点)时，浮体完全露出水面，排水量为0；当水平面通过v1(7号点)时，浮体完全淹没，排水量达到最大值。真实的水平面必然通过v0v1的连线(2号点和7号点的连线)。在v0和v1的连线上一定存在某点vt(xt，yt，zt)：当水平面通过vt，浮体排水体积V满足浮体平衡条件(Ⅰ)。

不妨令vt点的坐标为

(8)

式中：0≤t≤1。

可使用二分法求t，然后代入式(8)和(1)即可求出水平面方程。下面给出内层迭代法求水平面方程的流程图，如图7所示。

将t0代入式(8)和(3)计算水平面方程的4个参数，然后分析每个四面体与水平面的相交关系，计算每个四面体的排水量Vi(0)，最后汇总得到t0对应的浮体的排水量即得图7中V0：

(9)

同理，得到t1和tm对应的浮体排水量：

(10)

(11)

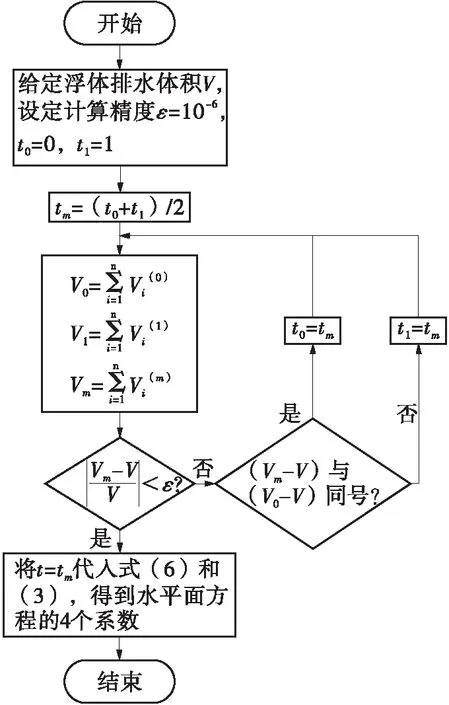
图7 内层迭代法流程图(模拟浮体升沉运动)

2.2 外层迭代(模拟旋转)

根据内层迭代法固然能够令浮体浮力=重量(平衡条件I)，但重力作用线与浮力作用线不一定重合(平衡条件II)。如图8所示，浮力作用线通过浮心B，方向与水平面法向N相同；重力作用线通过重心G，方向与N相反。令两条作用线之间的距离为l，如果l≠0，则水平面法向N将会绕某个轴Axis(假设浮体不动)旋转。可根据右手螺旋法则确定Axis：

(12)

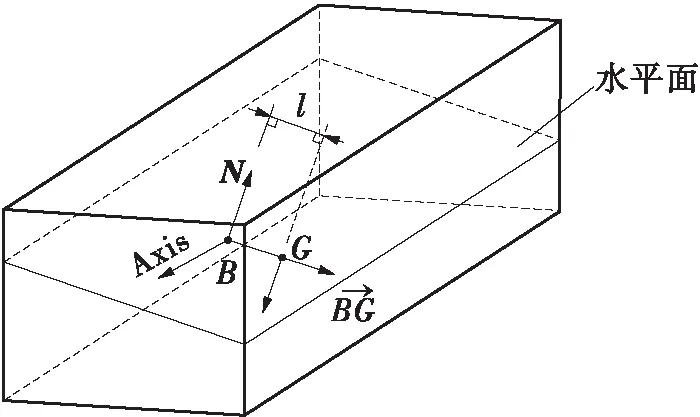
图8 浮体旋转轴

不妨假设初始状态下，浮体在水面处于正浮状态。浮体通过升沉运动(内层迭代法模拟)使得浮力=重力，但如果重力和浮力作用线不重合，那么浮力和重力形成的力偶将驱动浮体旋转(外层迭代法模拟)。假定浮体不动，水面旋转，则N绕Axis旋转，产生新的法线方向N′。通过内层迭代法再次模拟浮体沿N′的升沉运动，浮心B将移至新的位置B′，浮力和重力作用线之间的距离l将随之减小。如果l≠0，N′将继续旋转，l进一步减小……如此循环往复，直至l=0(或者小于指定误差)。

将以上过程进行模拟，得如图9所示的流程图。注意：这里假定浮体不动，N不断调整，直至收敛。

图9 外层迭代法流程图(模拟浮体旋转)

图9中，1)指定排水体积V和水平面法向N0，利用图7所示的内层迭代法求水平面方程，然后分析每个四面体和水平面方程的关系，最后汇总计算浮心B0；

2)当水面法线为N0时，计算通过B0的浮力作用线和通过G的重力作用线之间的距离l0；

3)根据浮心B0、重心G和水平面法向N0，计算浮体旋转轴Axis=B0G⊗N0；

4)N1=水平面法向量N0绕轴Axis旋转δθ1后的法向量(假设浮体不动，水平面法向量N0旋转)；

5)流程运行至此说明浮体绕Axis旋转，无论旋转角多小，也无法减小重力和浮力作用线之间的距离。其原因在于浮体重心过高，正在倾覆。浮体将绕Axis旋转1°。

3 算例

为验证文中方法，对某半潜式海洋平台模型(图10)进行浮态试验，然后使用商业软件Maxsurf和文中方法进行对比。平台主尺度如表1所示。

图10 半潜式海洋平台模型(单位：mm)

表1 半潜式海洋平台模型主尺度

平台构件包含：2个下浮体(如图11所示，每个下浮体由1个长方体和2个三棱柱组成)、2个横撑(如图12所示)和4根立柱(如图13所示)。6个长方体、4个三棱柱和2个圆柱体又可进一步分解为多个四面体，具体方法参考文献[7]。

图11 下浮体(单位：mm)

图12 横撑(单位：mm)

图13 立柱(单位：mm)

3.1 浮态实验

图14所示为模型在实验现场的初始正浮状态。因为制作误差，需在模型顶部安装平衡块。模型空载质量M=12.56 kg包含了平衡块，即图14圆圈内的片状压铁。平衡块使模型能够正浮在水面上，最终保证模型的重心恰好位于中纵剖面和中横剖面的交线上。将安装好平衡块并在水中保持正浮状态的模型从水中取出，晾干水后，在岸上通过一定的方法测出平台的重心高度为187.5 mm。

图14 初始正浮状态

再次将平台置于水中，将0.232 kg的压载(如图15所示)布置在平台顶部不同的位置：工况1为横倾(如图16所示)，压载位于2、3号柱之间；工况2为纵倾(如图17所示)，压载位于3、4号柱之间；工况3为任意倾斜(如图18所示)，压载位于1号柱上方。平台+压载的重心数据列于表2。3种工况下，测量各支柱标尺(如图17所示)位置的吃水，列于表3。根据文中提出的算法，编程(下载地址：www.huagongchuanhai.cn/tetrahedron)计算平台3种工况下各个支柱的吃水，计算值也列于表3。

图15 测量压载的质量

图16 2、3号柱之间的工况1(横倾)压载

图17 3、4号柱之间的工况2(纵倾)压载

图18 1号柱上方的工况3(任意倾斜)压载

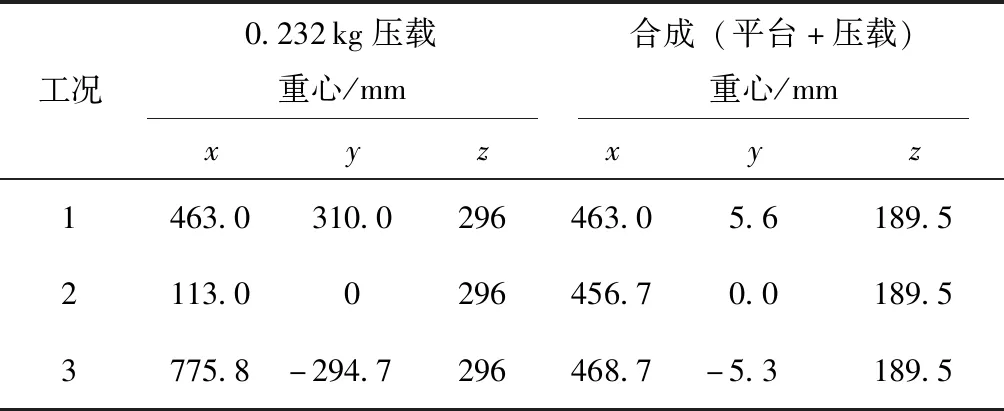
表2 各工况下的重心

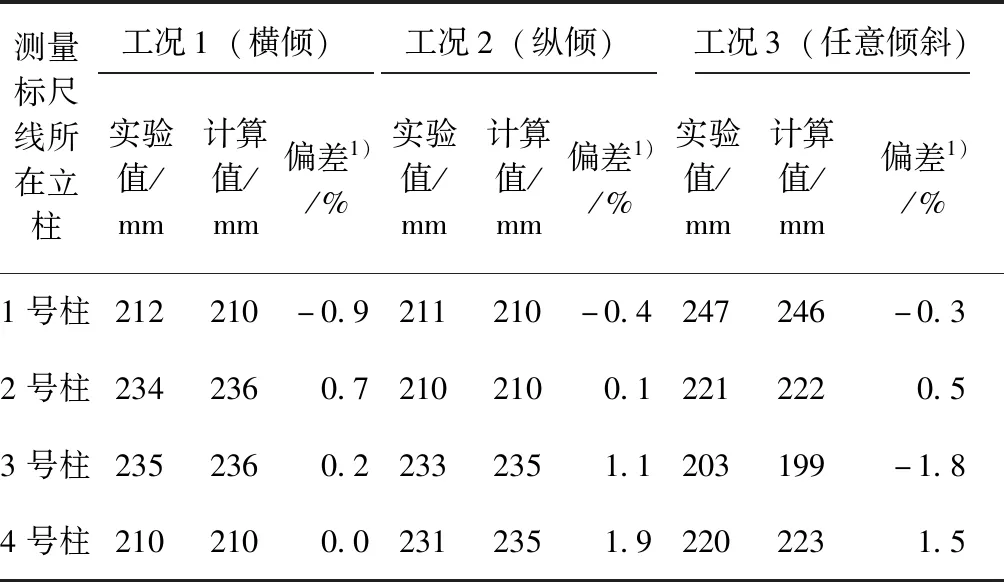
表3 立柱标尺线(图17)吃水实验值和计算值

如表3所示，实验值和计算值的最大偏差=1.9%，最小偏差=0.0%，平均偏差=0.2%。可认为文中算法在浮态计算方面是可靠的。

此外，为了验证算法的收敛性，将各工况每次外层迭代的l值(重力和浮力作用线之间的距离)列于表4之中，并绘制曲线(如图19所示)。观察工况1情况下l变化曲线，可发现两点规律：(1)仅经过2次迭代，l迅速从5.6 mm收敛至0.545 mm，收敛幅度达90.3%；(2)从第11次迭代开始，l即收敛至0.001 mm，达到工程精度要求。其它两种工况下的收敛也呈现出类似规律。

图19 重力和浮力作用线之间的距离变化曲线(外层迭代)

表4 重力和浮力作用线距离(外层迭代)

3.2 对比测试

为了进一步检测文中算法，针对表2和表3中的工况1(横倾)，使用商用软件Maxsurf建模进行浮态计算。

图20 Maxsurf模型(约50个剖面)

Maxsurf计算得到的浮心高度为81.90 mm，横倾角=2.0°。

采用文中算法得到水面方程4个系数：A= 0，B=-0.031 8，C=0.999 5，D=-222.694，浮心高度为75.35 mm，横倾角为arcsin(0.031 8)=1.8°。

由以上计算结果可知：在浮心高度和横倾角这两项指标上，Maxsurf与文中方法差异明显。下面用AutoCAD验证文中得到的水面方程是否满足精度要求。

如图21所示，利用文中算法得到的水面方程在AutoCAD中绘出水面，然后对平台进行切割，去除水上部分，最后使用AutoCAD的Massprop命令获得平台水下部分的质心(即平台的浮心)坐标为(463.000，9.222，75.359)。将文中算法得到的水面法线方向〈0，-0.031 8，0.999 5〉，AutoCAD 得到的浮心坐标以及给定的重心坐标代入式(4)，可得重力和浮力作用线的距离l=0.009 5 mm。在型宽为800 mm的情况下，不到0.01 mm的误差说明文中算法得到的水面方程非常接近“真实解”。

图21 去除水面以上部分的平台(AutoCAD建模)

Maxsurf计算得到的浮心高度为81.9 mm，“真实”浮心高度约为75.4 mm，8.6%的误差显然并不理想。如图22所示，如将Maxsurf的剖面数增加到200，计算结果75.1 mm趋近于理想值(如表5第2行所示)。不同的剖面数对Maxsurf精度产生影响的原因如图23所示：平台圆柱体是横向布的，当剖面数=50时，圆柱体直径方向上只布置了两个剖面(如图23(a)所示)，显然不够；当剖面数=200时，圆柱体直径方向上布置了足够多的剖面，故其体积计算精度令人满意(如图23(b)所示)。但是对于圆柱体附近的长方体而言，沿纵向布置2-3个剖面即可，没有必要布置太多剖面(如图23所示)。另外对于圆柱体，虽然只要沿船长(纵向)布置足够多的剖面(如图24所示)就可以达到必要的精度，但其实这是一种“暴力”计算(相当精度条件下，Maxsurf计算时间为1.92 s，而文中算法只需要0.26 s，计算机处理器主频 3.7 GHz)。更为合理的方法应当是沿圆周方向布置剖面(如图25所示)。但是Maxsurf“脱胎”于船舶性能计算，其浮态计算基于“剖面”的数值积分，弊端在于只能沿一个“统一”方向(船长方向)设置积分剖面(如图24所示)。文中基于四面体网格提出的浮态算法则不受此限制，可根据需要对浮体的每个构件进行合理地“独立”分网(如图25所示)。因此文中算法更适合分析“凸多面体”组合结构。

图22 Maxsurf模型(约200剖面)

表5 Maxsurf在不同剖面数目情况下的计算结果

(a)约50个剖面 (b)约200个剖面

(a)圆柱体剖切网格 (b)等效棱柱

(a)圆柱体剖切网格 (b)等效棱柱

4 结语

文中针对传统浮态计算方法应用于“凸多面体”组合结构存在的不足，提出了一种新的浮态计算方法，编制了程序，开展了物理和数值实验研究，并与传统方法进行了初步比较研究。文中完成的主要工作和得到的主要结论如下：

(1)提出了一种全新的浮态计算方法，通过内外两层迭代分别模拟浮体平衡过程中的升沉和旋转运动，具有明确的物理意义。相对于传统的矩阵迭代法，避免了繁琐的水面要素和水下体积要素的计算；同时也因为其具有明确的物理意义，避免了传统方法有时候无法收敛的缺陷。

(2)编制了相关的程序，同时针对某半潜浮式平台进行了建模和数值分析，还展开了实际的水池物理实验。为“凸多面体”组合结构的浮态计算和测量提供了有价值的参考。计算和实验数据表明：文中算法具有良好的精度和收敛性。

(3)利用著名的浮态计算软件Maxsurf对目标平台进行了建模和数值分析，将获得的关键浮态参数与文中方法进行了对比分析。对于二者产生分歧的地方，请来第三方CAD软件作为“裁判”。分析表明，对于“凸多面体”组合结构，文中算法更容易得到较为精确的结果。另外在达到同等计算精度的前提下，文中算法的收敛速度也比Maxsurf要快。

文中工作是对凸多面体组合结构浮态计算和测量的初步探索，其计算效率还有提升空间。利用有限元软件进行四面体网格剖分(图4)只是权宜之计。将来如果能够仿照“船舶曲面快速构建”这一思路，专门针对“浮体四面体网格快速剖分”提出相应的算法，相信一定能够从整体上提升算法的计算效率。