基于时间卷积神经网络的短时交通流预测算法

袁华 陈泽濠

(华南理工大学 计算机科学与工程学院，广东 广州 510640)

在智能交通系统(ITS)中，交通控制和交通诱导非常重要，而实时准确的交通流预测能为交通控制提供有效帮助，是实现交通诱导的基础。交通流预测就是根据大量交通历史数据来预测未来时刻的交通状况[1]，短时交通流预测能提供未来交通流信息，提高控制策略的准确性。对于实时交通诱导，如果仅仅依靠实时交通信息，引导出行者前往不拥堵的路段，可能导致不拥堵路段一段时间后发生拥堵，而先前拥堵路段反而已经疏通。短时交通流预测使得诱导具有一定的前瞻性，能更好地解决交通拥堵等问题。因此，短时交通流预测具有非常重要的现实意义。

本文中研究的交通流特指交通流量，是单位时间内通过道路某一断面的车辆总数。交通流量是量化交通通行能力的一种有效指标。目前，短时交通流预测方法可以分为两大类：模型驱动方法(Model-base Methods)和数据驱动方法(Data-base Methods)。其中，数据驱动方法又可分为：简单方法(Naïve Methods)、参数方法(Parametric Methods)、非参数方法(Non-parametric Methods)和混合方法(Hybrid Methods)。

模型驱动方法依靠理论假设和软件模拟来建模，难以应付交通所具有的社会性[2]；随机游走(RW)、历史均值(HA)等简单方法无需进行复杂建模计算而直接输出结果，没有考虑交通流的波动性[3]，难以应付越来越复杂多变的大型交通系统；参数方法根据一定的先验知识假定交通流符合特定的概率分布模型，进而根据训练集估算出模型参数，交通流预测上的经典参数方法为求和自回归移动平均模型(ARIMA)，但其计算复杂度高，难以胜任复杂多变的短时交通流预测，且预测精度明显不足；由于交通流数据的非线性以及随机性，很难对交通流分布作出任何假设，而非参数方法对总体分布不作假设，更适合短时交通流预测任务。且伴随数据规模的膨胀以及计算机速度的提升，非参数方法逐渐表现出优越性。混合方法就是将上述不同模型的结果有机地结合起来，以达到优势互补的效果。

近年来，短时交通流预测逐渐倾向于使用深度学习(DL)。Huang等[4]首次将深度学习应用于交通领域，设计了一个由两部分组成的深层架构，即底层的深度信念网络(DBN)和顶层的多任务回归层(MTL)，与当时预测效果最好的方法比有5%的提升，但该深层网络结构忽略了交通流时序数据之间的依赖关系；Lü等[5]将路网全部交通流量数据直接作为堆叠自编码器(SAEs)的输入，成功从交通流数据中发现潜在的交通流特征表示，如非线性时空关系，最终在中、重度交通状况下有很好的表现；Ma等[6]首次使用长短时记忆网络(LSTM)预测城市干道上的车流速度，LSTM能学习具有长时间依赖关系的时间序列，且无需指定时间延期；Duan等[7]介绍了一种基于多层降噪自编码器(SDAEs)在交通流数据填充上的应用；Fu等[8]首次将循环门控单元网络(GRU)应用于短时交通流预测，利用前半个小时的交通流预测下一个5 min的交通流。实验表明，GRU预测效果最好，其次是LSTM，ARIMA效果最差，这是GRU在短时交通流预测领域的简单尝试。

从上述文献来看，研究人员首先尝试在交通流预测领域运用深层网络结构，进而尝试使用不同方法来发现交通流序列中潜在的非线性关系。LSTM、GRU等循环神经网络(RNN)确实能很好地对序列进行建模。然而，循环神经网络本身存在梯度弥散(Vanishing Gradient)与梯度爆炸(Exploding Gradient)问题，LSTM、GRU等变体也仅仅只是对其梯度弥散问题的缓解。与此同时，循环神经网络因其独特的计算方式难以获得较高的训练效率。RNN每个时刻的输出都是对前一时刻输出执行相同操作而产生的，当前时刻的计算依赖于上一时刻的计算结果。这种固有特性使得RNN只能逐个时刻串行计算，难以并行化，更难以在GPU上有较好的加速效果。

Bai等[9]在2018年提出一种新型的时间卷积网络(TCN)。实验表明，尽管理论上RNN可以拥有无限长的“记忆”，但却难以训练，也难以并行。TCN相对于RNN具有以下优势：1.实际建模过程中可以有更长时“记忆”；2.TCN基于卷积神经网络，因而更易于并行。TCN不是一种单一的网络结构，而是一类基于卷积神经网络(CNN)改进的，用于解决序列问题的神经网络的总称，如WaveNet[10]是TCN模型的一员。WaveNet结合了扩张卷积[11](Dilated Convolution)与因果卷积[10](Causal Convolution)，使得感受野(Reception Field)变大，更好地对原始语音进行建模。You等[12]将TCN应用于推荐系统，提出了分层时间卷积网络(HierTCN)，召回率提高了18%，平均倒数排名提高了10%。

实际交通流容易受到诸如天气、赛事、事故等多种因素的干扰，当交通流出现明显上冲或者下跌时，需要及时根据历史数据调整模型，这对短时交通流预测模型的在线更新性能提出了较高要求。CNN允许并行进行卷积计算，使得CNN在GPU上有很好的加速效果。使用以CNN为基础的TCN，也就可以使用GPU大大加快模型训练过程，以保障模型的在线更新。

本文中首次将TCN应用于短时交通流预测领域，基于TCN的基本思想，保留扩张卷积与因果卷积，剔除残差网络(Residual Connection)，提出扩张-因果卷积网络(DCFCN)，在短时交通流预测任务上取得优于LSTM、GRU的效果，且在GPU上有明显的加速效果。

1 网络结构

1.1 时间卷积神经网络

1.1.1 扩张卷积

针对短时交通流预测等序列任务，需要对前一段时间内的交通流进行建模，不能仅仅依靠上一时刻交通流。而传统全连接神经网络在相邻层之间进行全连接，同一层的不同单元之间没有连接，这样的全连接结构只能学到数据之间的关联信息，而无法获取其序列信息。LSTM、GRU等RNN结构的网络通过内部存储单元将“记忆”固化，并向后传递，学习其序列信息。卷积神经网络可以通过卷积计算形成“记忆”，感受野的大小反映了使用多少数据生成“记忆”。在序列预测任务上使用卷积神经网络最大的问题是如何获取序列的长时记忆。

在卷积神经网络中，感受野指的是特征图(Feature Map)上的节点在输入图片上映射区域的大小。为了更好地获取长时记忆，关键就是扩大感受野。如图1所示，深色表示第3层某一节点可“看到”的区域。当卷积层数为l，每层卷积核大小为k时，感受野大小为(k-1)×l+1。卷积神经网络的感受野大小与卷积核大小、卷积层数呈线性关系。因此，增加卷积层以及增大卷积核均能扩大感受野。但更深的卷积层数以及更大的卷积核，使得网络参数量庞大，难以完成训练。将3个3×3卷积核进行堆叠，可以使其感受野与一个7×7卷积核的感受野大小相同，但3个3×3卷积核的参数量约为27C(C表示常数)，一个7×7卷积核的参数量是49C。在卷积神经网络中，通常偏向于使用不太大的卷积核，较大的卷积核会使得网络参数急剧增加，运算复杂度增加。另外，增大步长(Stride)或者增加池化层(Pooling)也可以更好地获取长时记忆，但有可能造成严重的信息丢失。

图1 感受野(k=3，l=2)

另外一种方法就是使用扩张卷积，与一般卷积相比，扩张卷积除了卷积核大小外，增加了用来表示扩张大小的扩张系数(Dilation Rate)。

扩张卷积的计算公式定义为

(1)

式中，d表示扩张系数，k表示卷积核大小。当d为1时，扩张卷积退化为普通卷积，通过控制d的大小，从而在计算量不变的前提下拓宽感受野。

图2中清晰展示了大小为3×3，扩张系数为2的卷积核在进行卷积计算时，与深色区域进行卷积计算，而忽略白色“空洞”。此时感受野大小为7×7。

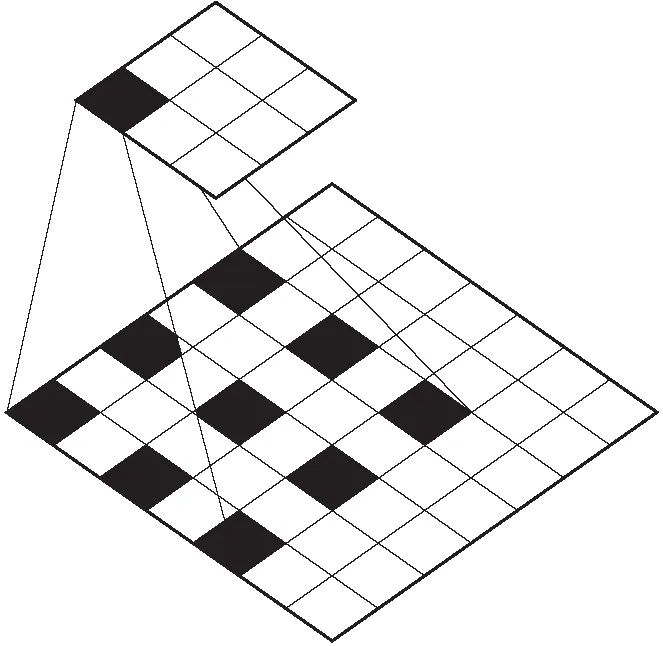
图2 扩张卷积

显然，扩张卷积会存在一定问题，当多次叠加相同扩张系数的卷积层时，可能使得部分时刻数据没有参与计算，忽略了这些时刻的信息，称为“Gridding”问题[13]。如图3所示，堆叠两层扩张系数为2的卷积层，将无法获取图中输入层白色部分信息。

图3 “Gridding”问题

因此，一般在设计扩张卷积时，随着网络深度的增加，扩张系数呈指数增大，这不仅确保了网络覆盖所有有效信息，也使得深层网络能够获取更长的有效信息。

1.1.2 因果卷积

扩张卷积很好地解决了“长时记忆”的问题，而因果卷积解决的是信息泄露问题。信息泄露是指针对交通流预测等序列处理问题，需要确保模型不能颠倒序列顺序，在模型预测t时刻时，不能使用t+1，t+2等未来时刻数据。而在传统的一维卷积神经网络中，卷积核对前后时刻数据进行卷积计算，这就不可避免地使用了未来时刻数据进行建模，也就是信息泄露。因果卷积在WaveNet中首次提出，在因果卷积中，t时刻的输出只与上一层中t时刻及更早时刻的输入进行卷积，而与t时刻之后的值无关。如图4所示。

图4 因果卷积

与传统卷积神经网络相比，因果卷积只能“看”到过去的数据，而“看”不到未来的数据，因此很好地解决了信息泄露。一维因果卷积一般通过Padding实现，序列前端填充相应位数的零，而序列末端不进行填充。

1.2 网络结构

本文基于TCN的基本思想，将上述扩张卷积与因果卷积进行结合，首次将TCN应用于短时交通流预测领域[14]。图5为本文中所提出的网络结构，第1层为交通流序列输入层，接下来连续堆叠6层一维卷积层，每层卷积层均通过Padding实现因果卷积，卷积核大小为4，卷积核个数为32，每层扩张系数分别为1、2、4、8、16、32，之后接入全连接层，输出下一时刻的交通流。图5虚线框内表示最后一层隐藏层，隐藏层之后为最终输出节点。

图5 DCFCN结构

具体步骤如下。

步骤1 首先将交通流序列数据以滑动窗口的方式进行处理，窗口大小为21，每次向前滑动一个数据，即时间步为21，预测下一个时刻的交通流大小；

步骤2 将滑窗处理后的数据进行预处理并划分训练集与测试集；

步骤3 将训练集输入DCFCN模型进行训练；

步骤4 利用训练好的模型预测测试集交通流大小并计算误差。

图6中展示了多层扩张-因果卷积堆叠的示意图，DCFCN扩张系数分别为1、2、4。扩张系数呈指数增长，使得感受野大小也呈指数增长，即使在少数卷积层的情况下，也能获得非常大的感受野，同时还保证了模型的计算效率。

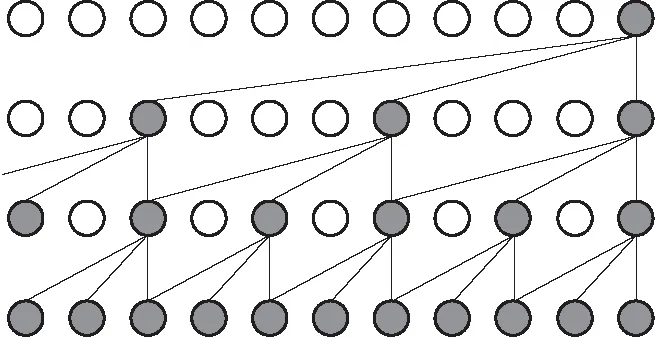
图6 多层扩张-因果卷积堆叠

卷积神经网络在卷积级中并行地计算多个卷积并生成一组线性激励的响应，因此可以使用GPU进行加速。每个线性激活响应都会经过一个非线性激活函数，如线性整流激活函数(ReLU)。本文中在ReLU激活函数之前进行层正则化(Layer Normalization)，将层输出值限制在0到1的区间。

2 实验

2.1 实验环境

为了对比不同模型在CPU以及GPU上的表现，文中将分别在CPU、GPU上进行实验，实验环境如表1所示。

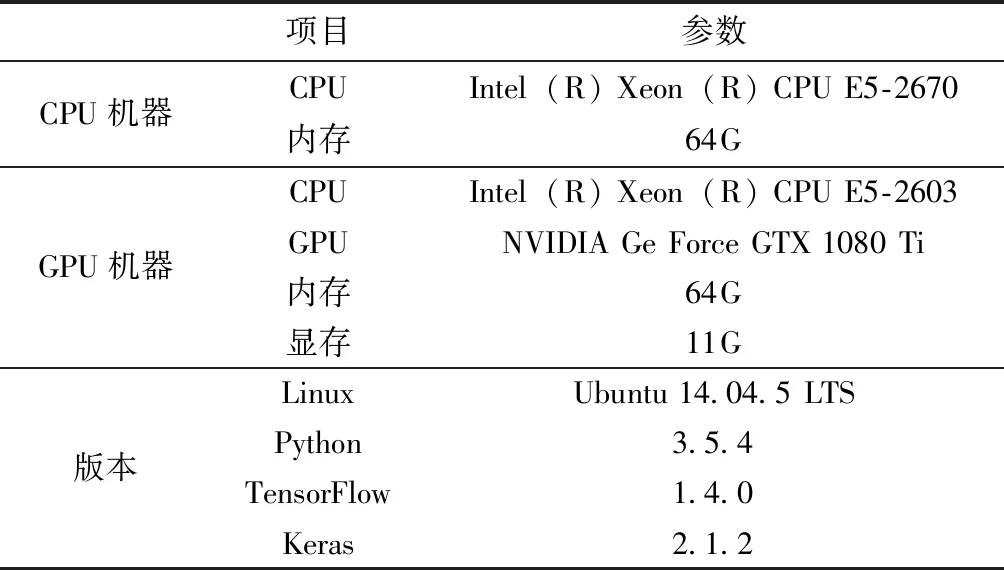
表1 实验环境

2.2 数据以及预处理

本文中实验数据来源于PEMS系统，随机挑选了8个不同位置检测器，编号分别为VDS 12139 63、VDS 1201453、VDS 1201637、VDS 1201671、VDS 1201705、VDS 1201735、VDS 1201751。获取每个检测器在2014年4月1日到2015年6月30日间的交通流量数据，其时间间隔为5min。图7为编号VDS 1213963检测器2015年6月22日到2015年6月28日一周内交通流变化情况。

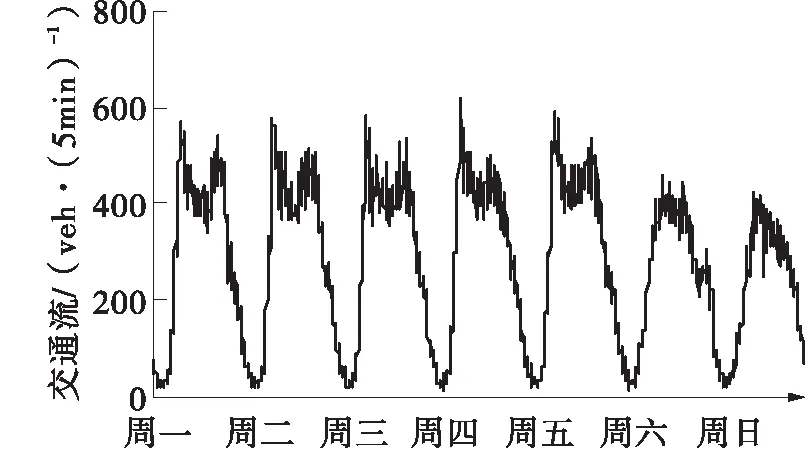
图7 一周内交通流

由于设备故障、噪声干扰、存储不当、人为过失等突发情况的发生，导致数据无法百分之百采集，存在错误数据和丢失数据。所以，在建立预测模型之前，必须对原始数据进行数据填充。数据填充的方法一般分为3种：预测、插值和统计学习[7]。预测方法通常是根据历史数据建立预测模型，并预测丢失数据；插值方法则是直接使用历史数据或相邻检测器数据填充丢失数据；统计学习方法是根据统计特征进行填充，通常先假设数据的概率分布模型，然后迭代估计模型参数。

本文中使用的是插值法，利用交通流的历史平均值进行填充。考虑到一周内不同日期的交通流模式不同，将交通流数据按周一到周日划分为7类，计算每一类中一天所有时刻的平均交通流，使用该平均交通流对缺失值进行填充。填充效果如图8所示，对编号VDS 1213963检测器在2014年3月8日的缺失数据进行填充，浅色部分表示填充的交通流曲线。

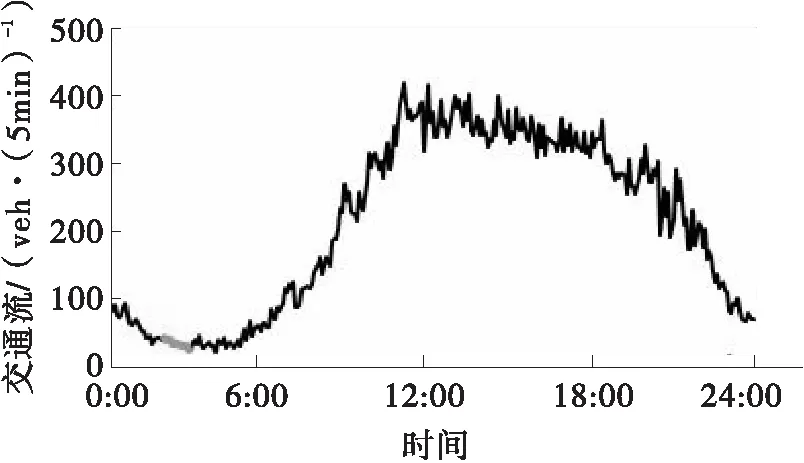
图8 数据填充

本文中采用最小最大归一化将数据映射到[0，1]区间，归一化公式如式(2)所示：

(2)

式中，z表示归一化后的数据，x表示原始数据，xmin为x的最小值，xmax为x的最大值。

2.3 评价指标

为了评价交通流预测模型的优劣，本文中将采用均方根误差(RMSE)为主要评价指标，同时辅以观察平均绝对误差(MAE)与平均绝对百分比误差(MAPE)的变化，在计算MAPE时，剔除零值样本。

(3)

(4)

(5)

2.4 数据划分

针对单一检测器，训练数据从2014年4月1日到2015年6月20日，预处理后总共128 361个完整样本，其中10%作为验证集，验证集大小为12 837；测试集从2015年6月20日到2015年6月30日，总样本量为2 946。

本文中在训练集上进行模型训练，并在验证集上验证不同参数下的模型效果，使得验证集上的RMSE最低。最后，不同模型在其最优参数下，使用同一测试集进行评测，比较模型性能优劣。

2.5 实验结果

2.5.1 实验设置

本节实验所使用的模型有随机游走、历史均值、ARIMA、LSTM、GRU、DCFCN，由于不同的超参数设置将会影响模型的预测精度，在保证尽量公平的前提下，文中通过查阅相关文献资料或者多次交叉验证得出不同模型的最佳参数。其中，LSTM、GRU与DCFCN的时间步均为21，与文献[15]保持一致。数据时间间隔为5 min。

具体参数设置如下：

(1) ARIMA分别取p=2，d=1，q=1，为了得到平稳的序列，预先做一次一阶差分。考虑交通流存在周周期性，当前时刻的交通流与上周同一时刻的交通流相似，差分使用当前时刻的交通流减去上周同一时刻的交通流；

(2) LSTM1和LSTM2分别表示使用单层LSTM与双层LSTM，隐藏层单元数为64；

(3) GRU1和GRU2分别表示使用单层GRU与双层GRU，隐藏层单元数为64；

(4) DCFCN每层的扩张系数分别为[1，2，4，8，16，32]，每层卷积核个数均为32，卷积核大小为4。

2.5.2 实验结果

本文中针对单检测器的短时交通流预测实验结果如表2所示，其中RMSE、MAE、MAPE均为10次实验后取平均值，S(RMSE)表示的是RMSE的样本标准差。

表2 实验结果

从表2中可以看出，相对于其他对比模型，本文提出的DCFCN预测效果最好，在RMSE、MAE、MAPE指标上均为最低。

LSTM与GRU能获取交通流序列的时序关系，预测效果优于简单方法以及传统的ARIMA模型，但仍不如DCFCN。DCFCN在RMSE上与单层LSTM相比降低了0.38，与双层LSTM相比降低了0.52，与单层、双层GRU相比均降低了0.38。说明TCN模型确实可以在序列建模上做得比RNN好。

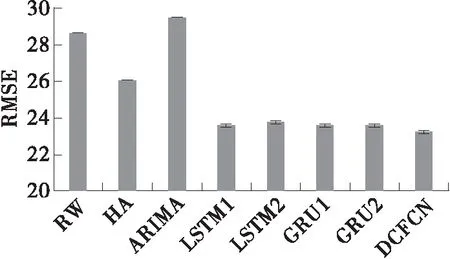
图9 不同模型RMSE对比

为了验证DCFCN模型是否在不同的检测器上均有效，选取了不同的检测器进行重复试验。表3中展示了不同检测器上不同模型的RMSE值。从表中可以看出，在随机选取的全部8个检测器中，6个检测器上DCFCN模型有最好的预测效果，本文中提出的DCFCN模型适用于绝大多数检测器。

表3 不同检测器实验结果

尽管在其中2个检测器上的预测效果不如LSTM或者GRU，但在保证预测效果的同时，DCFCN比其他模型有更快的训练速度。

LSTM、GRU等循环神经网络每个时刻的输出都是对前一时刻输出执行相同的操作而产生，这种固有特性使得RNN能具有“长时记忆”。也正是这种特性，使得RNN只能串行进行计算，而难以并行化，也无法使用GPU加速计算。而TCN基于卷积神经网络，不需要更新和保留“记忆”，输出之间不存在依赖关系，因此很容易并行化且能在GPU上进行更高效训练。表4中展示了不同模型的训练速度，CPU Time、GPU Time分别表示模型一轮迭代训练所需要的时间。从表中可以看出，LSTM与GRU在GPU机器上没有任何速度提升，甚至有所下降。原因是本文实验的GPU机器的CPU硬件资源不如CPU机器。而DCFCN模型在GPU机器上有明显的加速效果。

表4 训练速度

2.5.3 超参数分析

为进一步验证模型的有效性，考虑改变模型的网络结构参数，验证不同超参数对模型的影响。影响DCFCN模型预测精度的超参数主要有：激活函数、卷积核大小、卷积核个数、扩张系数、Dropout系数。实验结果如表5所示，实验过程中，除了对应超参数相应改变外，其他超参数保持不变，实验结果取10次均值。

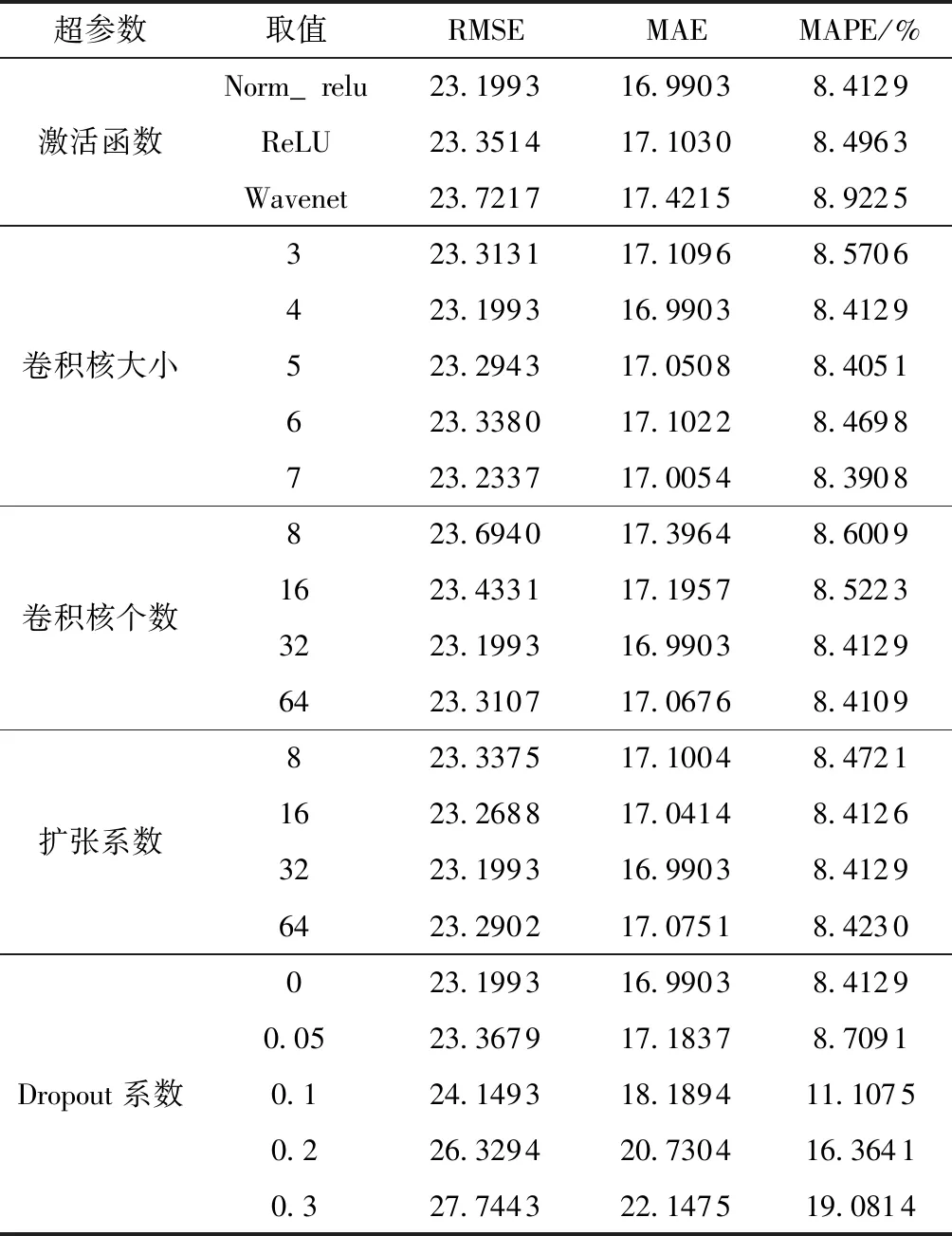
表5 DCFCN超参数分析

表5中，Norm_relu表示先对输出进行层正则化，再使用ReLU激活函数进行激活；Wavenet表示Wavenet模型中使用的激活函数，其本质是将神经元分别使用Tanh函数与Sigmoid函数激活后按位相乘。最终本文中使用的Norm_relu激活函数效果最好；另外，随着扩张系数的逐渐增大，模型精度先提升后下降，原因是扩张系数增大导致感受野变大，而感受野增大带来的好处就是能获取交通流更长的时序依赖关系。但是，随着扩张系数增大，网络层数逐渐加深，计算量与计算复杂度增加，导致模型更加难以训练，故模型精度反而有所下降。文献[10]中提及，当训练深层TCN模型时，应使用残差网络帮助训练。而残差网络的加入必然导致模型更加难以训练，故模型精度反而有所下降。文献[10]中提及，当训练深层TCN模型时，应使用残差网络帮助训练。而残差网络的加入必然导致模型训练时间增长且最优超参数更难搜寻。在DNN中引入Dropout可以有效地防止过拟合现象，但在DCFCN中移除神经节点的Dropout方式反而使得模型精度有所下降。

最终，当DCFCN激活函数为norm_relu，卷积核大小为4，卷积核个数为16，扩张系数为32，不引入Dropout机制时，取得的预测效果最好。

3 结语

本文中基于时间卷积神经网络基本思想，提出DCFCN模型，并将其应用于短时交通流预测。DCFCN由6层卷积层堆叠而成，每层通过Padding的方式实现因果卷积，扩张系数逐层呈指数增长。指数增长的扩张系数使得模型可以获取序列的长时记忆。实验结果表明，本文中提出的DCFCN预测效果优于LSTM、GRU等循环神经网络，证明了时间卷积神经网络在短时交通流预测上的可行性。与此同时，由于卷积神经网络天然易于并行，DCFCN在GPU上训练效率有明显提升。