基于累积误差平方和最小的参数估计方法
张英芝 翟粉莉 郑玉彬 朱继微 侯胜冬
(数控装备可靠性教育部重点实验室∥吉林大学 机械与航空航天工程学院,吉林 长春 130022)
自威布尔模型在产品的寿命研究中应用,关于两参数威布尔模型的参数估计问题就得到广泛关注。常用的威布尔模型参数估计方法有最小二乘估计、矩估计、极大似然估计、贝叶斯估计等。其中最小二乘法因对样本量没有要求且原理及计算简单,故在工程实际中得到较广泛的应用[1]。
应用中发现,经典最小二乘法估计参数虽满足无偏性,但因异方差的存在,使得回归模型不再显著[2]。故相关学者提出加权最小二乘估计,既满足无偏性又为最佳线性无偏估计,但余晓燕[3]通过数学证明该方法虽能在权重为各样本点扰动项方差的倒数时误差方差达到最小,但仍不满足有效性。
王永山[4]分析不同先验信息融合方法对贝叶斯参数估计精度的影响。刘正贤等[5]将威布尔分布转化为极值分布,再利用贝叶斯公式进行计算,虽简化了计算过程,但工作量仍然很大。Sawadogo等[6]针对运用牛顿迭代求解似然函数时的缺点,提出用遗传算法求解似然函数的方法,但因不同样本下似然函数表达式不同导致计算复杂度增加。Ehab等[7]研究了最大似然估计和贝叶斯估计在威布尔模型参数估计中的应用,发现不同样本下的参数估计模型推导难度较大,且不具有通用性。董力等[8]将遗传算法与最小二乘法结合进行威布尔模型参数估计,此方法虽减少数学计算过程,但不能弥补最小二乘法的不足。许伟等[9]提出基于混沌模拟退火的PSO算法求威布尔模型参数,该方法避免了精确解直接求解时的大量计算,但是其目标没有考虑经验分布函数,降低了估计精度。
综上可知,当前威布尔模型参数估计研究多考虑计算工作量或求解精确性,忽略模型总偏差。因此,借鉴智能算法与数学方程结合进行求解的研究方法,文中提出一种基于累积误差平方和最小的两参数威布尔模型参数估计方法,应用粒子群算法实现参数快速求解,采用柯尔漠哥洛夫-斯米尔洛夫检验(K-S检验)进行模型检验,用均方根误差(RMSE)来衡量参数估算精度。结合相关文献数据进行方法应用有效性证明。
1 威布尔模型
两参数威布尔模型的故障分布函数为
(1)
式中,β>0,α>0,β为形状参数,α为尺度参数。
对式(1)两边连取两次自然对数得:
ln[-ln[1-F(t)]]=β[ln(t)-ln(α)]
(2)
令
y=ln[-ln(1-F(t))],x=ln(t)
B=β,A=-βln(α)
(3)
可得回归方程:
y=Bx+A
(4)
2 累积误差平方和最小参数估计
2.1 目标函数及参数计算流程
文中以累积误差平方和最小作为目标构建参数估计模型,并结合完全样本、定时截尾样本与定数截尾样本情况进行具体参数估计。
目标函数为:
(5)
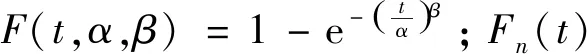
具体计算步骤如下:
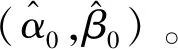
步骤2应用K-S法进行拟合性检验。
步骤3根据式(6)计算均方根误差,判断所提方法的优劣。判断标准为均方根误差值越大则表明参数估计精度越差[10]。
均方根误差计算公式为
(6)

文中对于同一类型可靠性数据,分别采用经典最小二乘法、加权最小二乘法以及基于累积误差平方和最小法3种方法进行威布尔模型参数估计,并计算均方根误差,以此为指标验证文中所提方法的有效性。
2.2 粒子群算法求解流程
粒子群算法(PSO)从鸟类捕食行为特征中得到启发并用于求解优化问题,算法中每个粒子代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值。在算法中每个粒子的速度都随自身及其它粒子移动经验进行动态调整,从而实现个体在可解空间中的最优。

算法中每个粒子代表一个潜在解,粒子数目一般取20-60,文中取40个粒子。根据参考文献[11- 12],设定粒子最大速度为0.8,设定粒子初始速度为0.8rand(1,2),rand(1,2)表示每个粒子随机产生一组2维速度初值。依据式(7)、(8)更新其速度与位置。在算法中设置算法的停止条件为迭代次数大于某一个数(MaxNum)。
(7)
(8)
式中,V表示速度,X表示位置,i代表第i个粒子,i=1,2,…,40,c1、c2为学习因子,分别代表粒子自身学习能力与全局学习能力,一般为非负常数,常取0-2,文中根据文献[12],取c1=c2=1.494。k为当前迭代次数,1≤k≤MaxNum;r1、r2为[0,1]内的随机数,d代表每个粒子的第d个估计参数,估计参数个数为2,故d=1,2,分别代表尺度参数与形状参数,Pi、Pg分别为个体极值与群体极值。
粒子群算法的步骤如下:
步骤1初始化粒子群的数目,设定学习因子值、粒子位置与速度。
步骤2根据式(5)计算个体适应度值,将个体最优值(p_ibest)设为群体最优值(p_gbest)。
步骤3依据式(7)、(8)更新粒子速度与位置,并计算新位置上个体的适应度值。
步骤4取粒子当前适应度与个体极值p_ibest适应度的最小值,将其赋值给p_ibest,并记录当前参数值。
步骤5对比个体极值p_ibest与群体最优值p_gbest值,若个体适应度值更小,则将其赋值给p_gbest,反之保持p_gbest不变。
步骤6若迭代次数小于设定值,则返回步骤3,否则,算法结束,同时输出最优参数值。
2.3 经验分布函数
(1)完全样本下经验分布函数
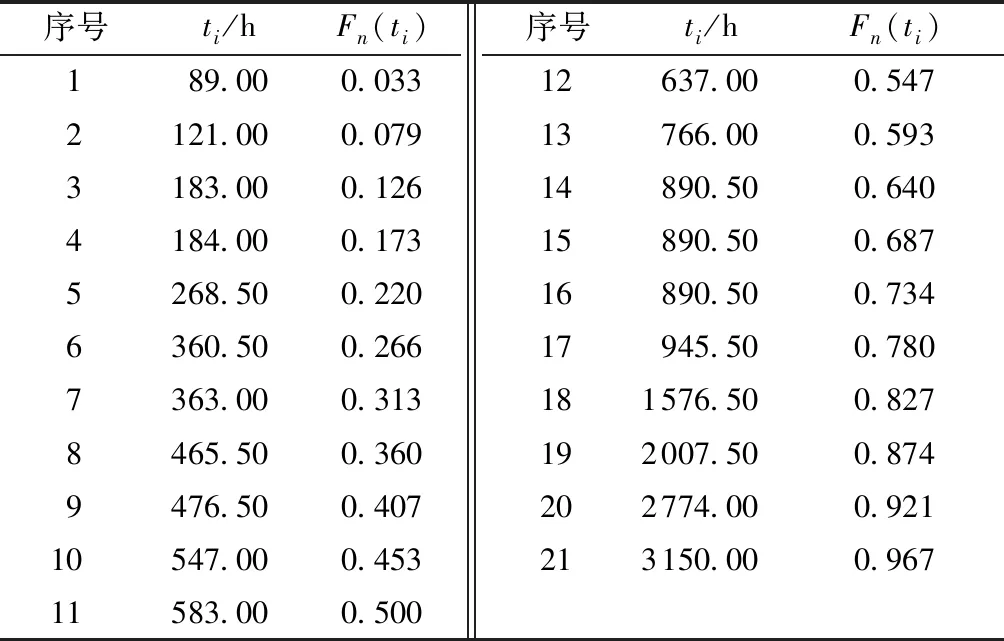
将n个完全样本的故障数据按从小到大排序,则t1 (9) (2)不完全样本下经验分布函数 1)定时截尾样本经验分布函数 设N为参加试验样品个数,定时截尾试验下产生n个故障数据和N-n个截尾数据。 为修正截尾数据对故障数据秩次影响,采用Johnson法,引入秩增量修正秩次变动。 设At(i-1)为第i-1个故障数据t(i-1)秩次,定义At0=0;j为所有N个数据从小至大的排列秩次,即j=1,2,…,N。 第i个故障数据ti的秩次Ati为 秩次修正后的经验分布函数计算公式为 (11) 2)定数截尾试验下经验分布函数 设n为参加试验样品个数,定数截尾试验下产生r个故障数据。文中采用“残存比率法”来估计定数截尾样本下产品在一定时间区间内残存概率,各故障时刻产品可靠度值,进而计算经验分布函数。 S(ti)为产品在时间区间(ti-1,ti)内残存概率,计算式为 (12) 因此,产品在ti时刻的可靠度R(ti)可表示为 R(ti)=R(ti-1)S(ti) (13) 式中,R(ti-1)为产品在ti-1时刻的可靠度,且R(t0)=1。 (14) 文中采用文献[13]中滚动轴承208在载荷为 606 N,转速为4 000 r/min的条件下,21个样本寿命时间与经验分布值如表1所示。 表1 轴承寿命时间与经验分布值 采用经典最小二乘法、加权最小二乘法及基于累积误差平方和最小法得到参数估计值,如表2所示.3种参数估计方法的K-S检验值(Dmax)和均方根误差如表3所示。 表2 完全样本威布尔模型参数估计值 表3 均方根误差和K-S检验值 显著性水平α=0.1,查表得K-S检验临界值为0.258 6,即3种估计方法均通过检验,表明滚动轴承寿命服从两参数威布尔分布。 由表3可知,基于累积误差平方和最小的参数估计法明显优于其他两种方法,且较最小二乘法、加权最小二乘法估计精度分别提高24.94%、8.23%。 将3种参数估计法得到的可靠度函数与近似中位秩公式所求经验可靠度函数绘图,如图1所示。 图1 完全样本可靠度曲线 文中参考文献[13],16个机电元件试验持续 1 510 个工作周期,其中有10个元件失效。根据平均秩次法计算得各元件的经验分布值,如表4所示。 表4 元件失效时间与经验分布值 同理计算得到参数估计值如表5所示,RMSE与Dmax如表6所示。查表得3种估计方法均能通过假设检验,表明机电元件的寿命服从两参数威布尔分布。 表5 定时截尾样本威布尔模型参数估计值 由表6可知,基于累计误差平方和最小法的参数估计精度最高,较其他两种算法精度分别提高97.44%和37.18%。 表6 均方根误差与K-S检验值 将3种方法的可靠度函数与经验可靠度函数绘图,如图2所示。由图2可知,3种估计方法得到的可靠度随着时间的推移偏差逐渐增大,但应用累积误差平方和最小的参数估计法得到的可靠度与经验可靠度是最接近的。 图2 定时截尾样本可靠度曲线 表7 样品失效时间与经验分布值 文中参考文献[13],13件样品做寿命试验,当失效数r=10时停止试验。失效时间以及根据残存比率法计算得到的经验分布值如表7所示。同理计算得到参数估计值如表8所示,RMSE与Dmax如表9所示。查表得3种估算方法均能通过假设检验,表明该样本的寿命服从两参数威布尔分布。 表8 定数截尾样本威布尔模型参数估计值 从表9可知,基于累积误差平方和最小参数估计法的精度最高,较经典最小二乘法和加权最小二乘法精度分别提高1.72%和1.15%。 表9 均方根误差与K-S检验值 根据定数截尾样本下3种参数估计法得到的可靠度函数与近似中位秩公式所求经验可靠度函数绘图,如图3所示。 图3 定数截尾样本可靠度曲线 图3表明,定数截尾样本下3种参数估计方法得到的可靠度函数随着时间的推移差别逐渐增大,基于累积误差平方和最小法的参数估计精度最高。 (1)文中提出的以累积误差平方和最小为目标的威布尔分布参数估计法考虑样本拟合分布函数与经验分布值的误差,可弥补经典最小二乘法与加权最小二乘法的不足。 (2)引入粒子群算法进行基于累积误差平方和最小的威布尔分布参数估计,避免大量数学推导过程,原理清晰易于理解,便于推广应用。 (3)文中将研究方法结合参考文献的3种样本数据进行应用,K-S检验值与均方根误差值表明,基于累积误差平方和最小的威布尔分布参数估计方法是合理与有效的。


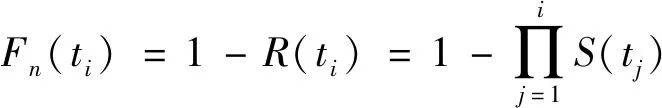
3 演算验证
3.1 完全样本



3.2 定时截尾样本数据





3.3 定数截尾样本数据



4 结论

