体外束锚下张拉力反张法测试机理及应用
郭文龙 单成林 梁鹏
(1.长安大学 公路学院,陕西 西安 710064;2.山西省交通科技研发有限公司 桥梁工程防灾减灾山西省重点实验室,山西 太原 030032;3.华南理工大学 土木与交通学院,广东 广州 510640)
锚下张拉力作为体外预应力桥梁施工中最重要的参数之一,对于保障桥梁安全和耐久具有重要的意义[1- 2]。《公路桥涵施工技术规范》中规定:同一断面中的预应力束其有效预应力的不均匀度应不超过±2%[3],《公路工程质量检验评定标准》中要求检查钢束中每根或每束钢绞线的张拉应力值[4],但对于如何随机抽检施工过程中已锚固钢绞线的张拉力及其不均匀度,并未给出明确方法。对于体外预应力钢束拉力的检测,目前主要参考斜拉索索力检测的动测频率法[5],但由于体外预应力钢绞线一般索长较短,频率法对这种短索结构测试误差较大。文献[6]、文献[7]分别介绍了磁通量技术和声发射技术,但由于受到试验环境条件的限制,测试精度离大规模推广应用还有一段距离。文献[8]中提出了钢束横张增量法,该技术是专利产品,目前商业化推广应用不多。文献[9- 10]将反张法应用在体内预应力钢绞线锚下张拉力检测中,介绍了一些定性的经验和规律,但对于反张过程中锚具内外侧钢绞线的应变重分布问题,以及测试误差的定量分析等问题并未作过多讨论。文献[11- 13]通过反张法测试了钢绞线夹片与锚具的咬合力,并给出了简易估算公式,但该方法对于任意规格锚固系统的普适性还有待进一步积累试验数据。总之,虽然目前体外预应力钢绞线锚下张拉力的检测有一些相关的测试方法,但具体检测机理和测试结果的定量判定准则,及其严谨性仍有待进一步验证。
文中从力学平衡和变形协调条件出发,从理论上推导了反张法测试体外束锚下张拉力的力学原理和误差影响因素,并对其适用条件和最大理论测试误差进行了深入分析。最后,结合施工现场中最常用施工机具和设备,提出了一种非常实用的测试方法和系统组成,并结合室内静载锚固试验机对测试方法进行了详细验证。试验结果表明,本文中提出的测试分析原理和实用检测技术稳定性好,测试误差能够满足工程精度的要求。
1 测试原理及适用条件
1.1 测试分析原理
钢绞线与混凝土结构的作用原理在教科书和有关文献[14- 19]中已经有详细介绍,但由于反张法中千斤顶的张拉力包括体外预应力钢绞线的锚下张拉力和锥形锚具与夹片的反向摩擦力,而锥形锚具与夹片的反向摩擦力目前还没有可靠的计算方法。为了便于分析,根据文献[20- 22]的有关基本概念,假定L内为锚固点之间体外预应力钢绞线张拉变形后的长度,L0内为与L内长度对应的钢绞线的无应力长度,ΔL内=L内-L0内,F内为锚固点之间钢绞线的锚下张拉力,ε内为与F内对应的锚固点之间钢绞线的平均应变;L外为夹片即将拉脱临界状态时近端永久锚具外侧与千斤顶夹持点之间钢绞线张拉变形后的长度,L0外为与L外长度对应的钢绞线的无应力长度(即近端锚具外侧钢绞线张拉前,千斤顶夹持点到永久锚具外侧之间的距离,也可以称为千斤顶张拉时的有效工作长度),ΔL外=L外-L0外,F外临界为夹片即将拉脱前临界状态时千斤顶的张拉力值,ε外临界为与F外临界对应的永久锚具外侧与千斤顶夹持点之间钢绞线张拉变形后的平均应变;Fμ为锚具与夹片的反向摩擦力,F滑移稳定为夹片与锚具拔脱后钢绞线应变重分布达到稳定状态时刻千斤顶的张拉力值,ε滑移稳定为与F滑移稳定对应的锚具内外侧钢绞线发生应变重分布后的平均应变,K为体外束锚下张拉力最大理论测试误差,As为钢绞线的面积,Es为钢绞线的弹性模量。如图1所示。
根据力学平衡和变形协调条件,由图1可知。

图1 夹片即将拉脱临界状态时钢绞线受力示意图
1)当夹片与锚具之间即将拉脱前临界状态时
当夹片与锚具即将拉脱前临界状态时,二者之间并未发生滑移,锚具内外侧钢绞线之间存在较大的应变差值,且二者应变相互独立,未发生应变重分布现象,根据文献[20- 22]的有关定义可得,
(1)
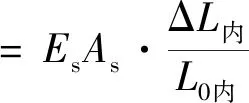
(2)
(3)
(4)
(5)
F外临界=F内+Fμ
(6)
F内=F外临界-Fμ
(7)
2)当夹片与锚具之间拉脱后钢绞线应变重分布达到稳定状态时
由无应力状态法可知,线弹性状态下千斤顶夹持点与远端锚具之间钢绞线的无应力长度在整个受力过程中是不变的,即L0=L0内+L0外;但是夹片与锚具拉脱后千斤顶夹持点与远端永久锚具之间距离(即钢绞线受力后的长度L滑移稳定)与近端锚具内外侧钢绞线的应变能重分布过程,以及千斤顶进油速率和行程变化密切相关。由于千斤顶进油速率涉及到机械控制和现场操作的复杂性,还无法简单地按经典的力学平衡或应变能守恒原理来求解精确的“钢绞线受力变形后的长度L滑移稳定”。根据文献[9]和文献[11]的试验结论,以及作者多次试验结果(详见图4、图7、图10)发现:在夹片与锚具拉脱临界状态前后,千斤顶与永久锚具间的位移突变幅度一般都在毫米量级,这对于被测体外束长度一般为米级(预应力混凝土桥梁的跨径一般大于10 m)的钢绞线来说,夹片拉脱前后L滑移稳定的突变增量影响极小。
为了便于得出能够指导现场检测的定量规律,本次分析时忽略夹片拉脱前后千斤顶夹持点与远端永久锚具之间距离突变影响的次要矛盾,假定当夹片与近端锚具之间拉脱后钢绞线应变重分布达到稳定状态时,千斤顶夹持点与远端锚具之间钢绞线变形后的总长度与临界状态时相等,即L滑移稳定≈L内+L外(本文中第4.1节将对L滑移稳定取值的合理性展开进一步深入讨论)。由于夹片拉脱前后千斤顶夹持点与远端永久锚具之间钢绞线的无应力长度是不变的,即L0=L0内+L0外,所以,ΔL滑移稳定=L滑移稳定-L0。根据线弹性状态的叠加原理[21- 22],夹片与锚具拉脱后钢绞线应变重分布稳定状态时的平均应变为
(8)
将式(2)、(3)代入式(8)得:
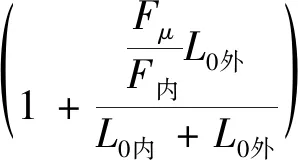
(9)
F滑移稳定=ε滑移稳定EsAs
(10)
由于反张时锚具与夹片的反向摩擦力缺乏有效的计算方法,还无法直接按式(7)得出钢绞线的锚下张拉力。因此,须对夹片与锚具的反向摩擦力Fμ占锚具与夹片滑移稳定时刻的千斤顶张拉力F滑移稳定的比例开展深入讨论。
1.2 反张法测试体外束张拉力的适用条件
由于夹片是通过千斤顶反拉钢绞线时,随着钢绞线从锥形锚具内拔出的,所以夹片与锚具的最小摩擦力为0 kN,最大摩擦力不超过钢绞线的极限拉力Fμmax=σmaxAs=1 860As。鉴于不同桥梁的设计参数、材料,以及不同厂家千斤顶的规格均不完全相同,为了安全起见,根据经验,取常规桥梁设计中钢绞线张拉控制应力σk=1 395MPa损失20%左右作为体外束锚下实际应力,即F内=0.8σkAs=1 116As,由式(1)和式(4)可知,当Es=1.95×105MPa时,L0内=0.994L内,所以:
①当夹片与锥形锚具之间拉脱后钢绞线应变重分布达到稳定状态时,且夹片与锚具反向摩擦力最小为0时,Fμ=0,F外临界=F内。此时,在夹片与锚具拔脱临界状态前后,永久锚具内外侧钢绞线应变相等,不存在应变重分布效应,即:F内=F外临界=F滑移稳定,所以,结合式(7)可得:
F内≤F滑移稳定
(11)
②当夹片与锥形锚具之间拉脱后钢绞线应变重分布达到稳定状态时,且夹片与锚具摩擦力最大时,将Fμmax=1 860As、F内=1 116As和L0内=0.994L内代入式(9)可得:
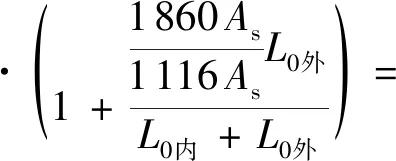

(12)
因此,当夹片与锥形锚具之间拉脱后钢绞线应变重分布达到稳定状态时,千斤顶拉力与锚下张拉力的最大理论误差K为

(13)
由①、②可见,虽然体外预应力钢束的锚下张拉力F内无法直接按式(7)求得,但结合式(13)可知,当夹片与锥形锚具之间拉脱后钢绞线应变重分布达到稳定状态时刻,
F滑移稳定≤(1+K)F内
(14)
由式(11)和式(14)可知,当夹片与锚具反向摩擦力最小时,F内≤F滑移稳定;当夹片与锚具反向摩擦力最大时,F滑移稳定≤(1+K)F内。表明虽然F滑移稳定的精确值还缺少可靠的计算方法,但是该参数在夹片与锚具摩擦力最不利条件下的上下极限值与体外束的锚下张拉力F内之间存在密切的关系。因此,可根据高等数学中极限存在的夹逼准则[23]的概念,建立起F滑移稳定与F内之间的相互关系,即
F内≤F滑移稳定≤(1+K)F内
(15)
由式(15)可知,F滑移稳定的大小是介于F内和(1+k)F内之间的物理量,当K值足够小时,可以得出能够满足工程精度要求的F滑移稳定≈F内。同时由式(12)、(13)可知,夹片与锚具拔脱滑移稳定时刻钢绞线的平均应变ε滑移稳定主要与体外束两端锚固点的距离L内,以及钢绞线反张前千斤顶夹持点到永久锚具外侧之间的距离(即千斤顶实际工作长度)L0外有关,最大理论测试误差K与锚固点距离,以及千斤顶的实际工作长度L0外[18]的变化规律如图2所示。
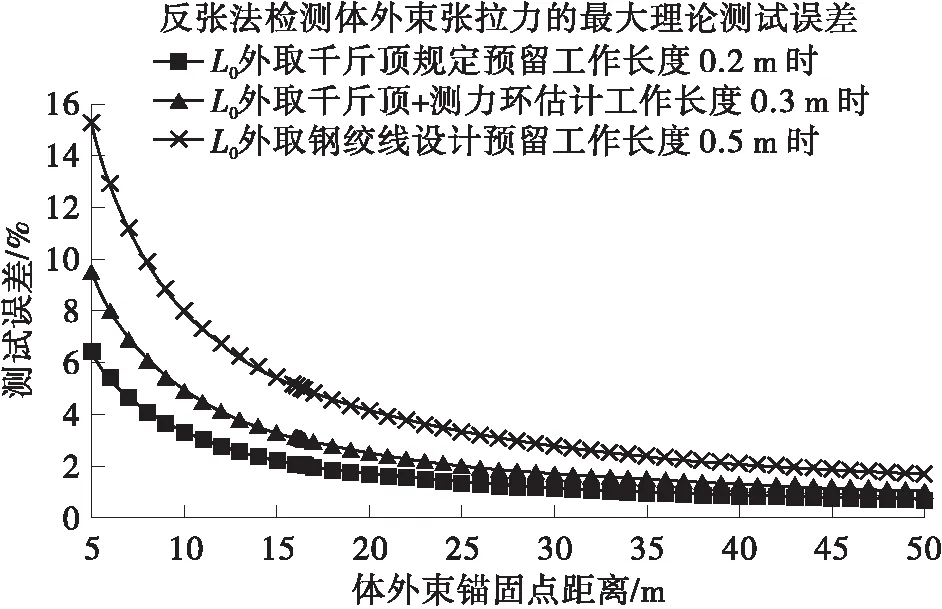
图2 锚固点距离-最大理论测试误差变化曲线
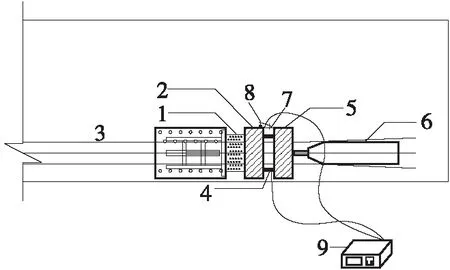
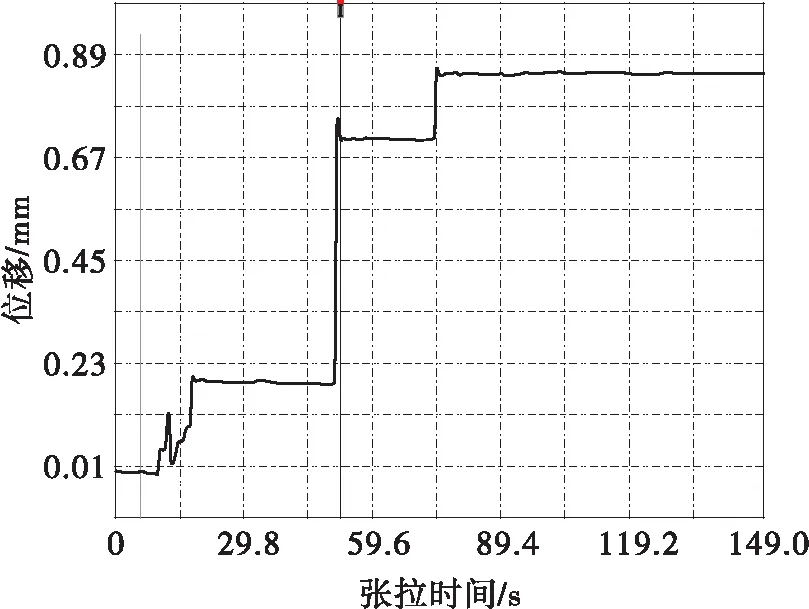
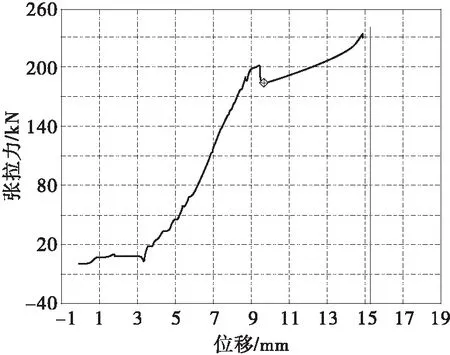
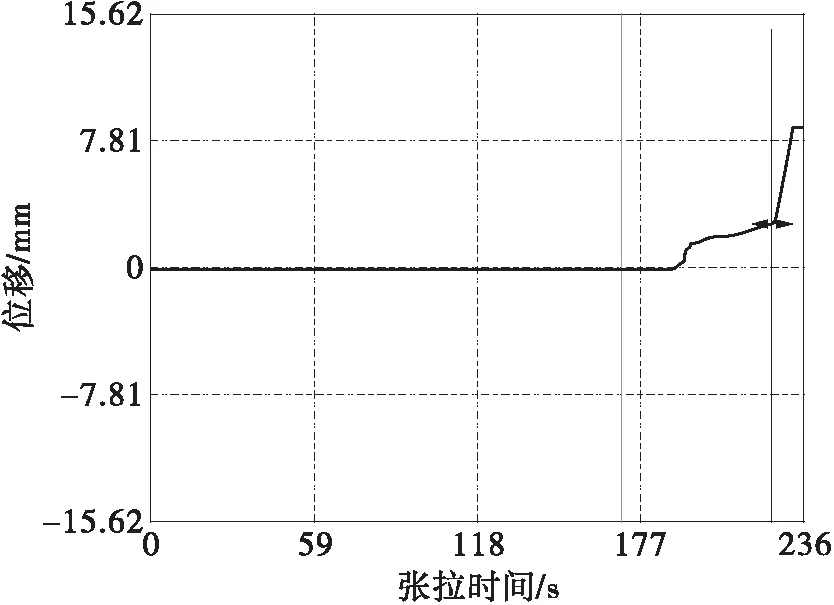
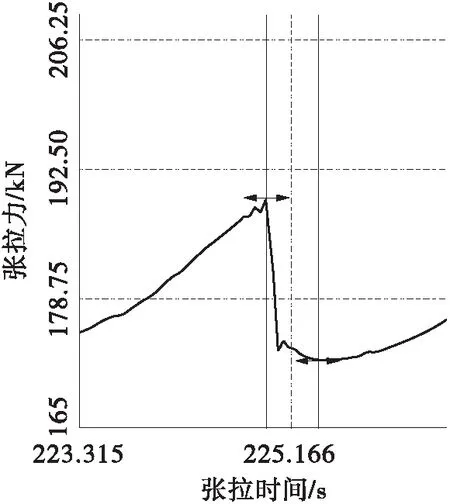
图2中方法一L0外取0.2 m时,是指千斤顶外伸活塞直接顶住永久锚具外侧张拉时,该方法的L0外即为千斤顶的夹持点到近端永久锚具外侧的距离(本文中取文献[24]规定的L0外=0.2 m);图2中方法二L0外取0.3 m时,是指本文建议的千斤顶+测力环时(由图3可知),此时L0外为千斤顶实际的工作长度+测力环和临时锚具的厚度(本文中取L0外≈0.2 m+0.1 m=0.3 m);图2中方法三L0外取0.5 m,指的是按一般图纸设计的钢绞线的预留工作长度0.5 m,显然L0外方法一 同时由图2可发现,方法1中锚固点间距大于6.51 m时,最大理论测试估算误差K不超过5%,但该方法需要千斤顶本身的张拉力和位移具有实时采集功能;方法2中锚固点间距大于9.76 m时,产生的最大理论测试估算误差K不超过5%;方法3中体外束锚固端距离大于16.26 m时,最大理论测试估算误差K不超过5%,由于任何规格穿心千斤顶的实际工作长度都远小于0.5 m。所以,本文中推荐的测试方法适用于任意锚固点间距大于16.26 m的体外预应力混凝土桥梁,基本满足锚固点间距大于9.76 m的体外预应力混凝土桥梁。即 F内≤F滑移稳定≤1.05F内 (16) 显然,式(13)中的最大理论测试误差是根据一般工程设计和施工经验,按各因素均最不利条件下可能产生的最大误差结果,并不代表每次测试过程中实际发生的误差。同时也表明,采用反张法测试体外束锚下张拉力的适用条件为主梁跨径不宜小于16.26 m,特别是体外束锚固点间距不应小于9.76 m。这对于绝大部分预应力混凝土公路桥梁均可适用。 为了验证反张法检测体外束锚下张拉力的测试精度,了解该方法检测过程中夹片与锚具拔脱临界时刻对不同参数曲线的敏感性,本文中在室内静载锚固试验机一侧锚固端处,利用平时施工梁厂中最常用的设备经过组装,进行了3组试验,具体试验方法和设备组成如下(详见图3所示)。 1—钢绞线原永久性锚具;2—夹片限位器,3—待测的单根钢绞线;4—测力环;5—与永久锚具相同规格的临时性锚具;6—穿心千斤顶;7—位移计;8—固定位移计的磁性表座;9—桥梁动态数据采集仪 Fig.3 Test installation diagram of the single strand tension 试验过程中将永久性锚具外侧的钢绞线依次穿入限位器、测力环、临时性锚具和千斤顶,安装并固定磁性表座和位移计,最后接入桥梁动态数据采集系统,开始测试。本次试验主要测试永久性锚具与临时锚具之间的相对位移变化,以及测力环的受力变化规律。试验参数如表1所示。 表1 试验参数 本次在室内静载锚固试验机上进行了3组单根张拉钢绞线的反张试验,数据采集频率为200 Hz,具体试验结果如图4-图12所示。测试误差及夹片拔出临界状态判定难易程度分析如表2所示。 图4 第1组位移时程曲线 图5 第1组张拉力时程曲线 图6 第1组力-位移曲线 图7 第2组位移时程曲线 图8 第2组张拉力时程曲线 图9 第2组力-位移曲线 图10 第3组位移时程曲线 图11 第3组张拉力时程曲线 图12 第3组力-位移曲线 由以上力和位移时程曲线,以及力-位移曲线可以看出,力-位移曲线的斜率对整个测试过程中力和位移变化最为敏感,曲线突变点更容易判断。 其中第1组和第3组按力-位移曲线的判断结果与张拉力时程曲线基本一致,第2组比按张拉力时程曲线的判断结果小0.9%,这主要是由于本次实验的曲线突变特征点采用手工点击鼠标捕捉,若采用具有自动捕捉疑似特征点功能的方法,同一组实验结果应该完全一致。第1组实验的实测张拉力为85.09 kN,比静载锚固试验机张拉力少6.6%;第2组实验的实测张拉力为183.49 kN,比静载锚固试验机张拉力大0.7%;第3组实验的实测张拉力为171.22 kN,比静载锚固试验机张拉力大1.2%。其中第1组试验结果误差较大的主要原因是由于该组实验的钢绞线张拉力过小,而且室内静载锚固试验机的有效工作长度只有约4 m,测试误差稍大;第2组和第3组实验测试误差均小于5%,基本满足工程精度要求。 表2 测试误差及夹片拔出临界状态判定难易程度分析 由式(8)、(9)可知,文中在夹片与锚具拉脱后钢绞线应变重分布达到稳定状态时,体外束钢绞线应变重分布计算中,钢绞线受力变形后长度采用夹片与锚具即将拉脱前临界状态时的值,该取值方法是否合理关系到锚下张拉力的最大理论误差K值分析的严谨性,因此有必要进一步展开深入分析。 文献[9]中指出:当千斤顶带动钢绞线与夹片沿轴线移动0.5 mm时,即测出锚下有效预应力值;文献[11]中的试验结果显示当永久锚具外侧钢绞线伸长超过4.5 mm时,夹片会脱离原有咬痕拉脱。从本文中试验结果的图4、图7和图10可以看出,夹片与锚具拉脱前后临时锚具与永久锚具间的位移突变量均为毫米量级,最大未超过 10 mm。由于千斤顶、锚具、测力环、主梁(本次试验为静载锚固试验机)等整个测试系统自身轴向抗压刚度相对于被测钢绞线来说是极其高的,测试系统自身弹性变形突变的细微影响几乎可以忽略不计,因此,可以认为千斤顶夹持点与远端永久锚具之间距离(即钢绞线受力变形后的长度L滑移稳定)的突变量值基本为毫米量级。本次室内试验时,千斤顶夹持点到静载锚固试验机远端锚具的距离约为4 m,若假定L滑移稳定的最大突变量值为10 mm,L滑移稳定的突变误差不超过0.25%;如果按本文要求的永久锚具锚固点间距必须大于9.76 m时,夹片与锚具拉脱临界状态前后,L滑移稳定值的突变不超过0.1%,基本不影响锚下张拉力的最大理论误差K值的估算精度。因此,采用反拉法测试体外束锚下张拉力时,夹片与远端锚具在拉脱前后的距离突变量可忽略不计,即L滑移稳定≈L内+L外。 当主梁原有锚具中钢绞线与夹片拔脱后,由于近端锚具内外侧钢绞线的应变有较大差异,二者的应力水平会发生重分布而达到新的平衡状态。具体突变段曲线(详见图13两竖向光标之间的部分)中哪个时刻的代表值能够反映锚下钢绞线拉力的真实值是一个需要思考的重要问题。 由图1和式(15)可知,当夹片与锚具拔脱时刻,千斤顶张拉力的最小值不会低于体外束锚下张拉力的大小。同时根据图2可知,当体外束锚固端距离大于一定距离后,千斤顶的张拉力与体外束锚下张拉力的最大理论误差不超过5%。所以,采用反张法测试体外束锚下张拉力时,千斤顶的张拉力值应取夹片与锚具拔脱临界时刻的下限稳定值。 由图13中张拉力时程曲线可知,在主梁锚具与夹片拔脱临界时刻,大部分曲线中突变曲线下限稳定值附近会先出现微小波动现象,然后测试结果才趋于平衡,再继续匀速稳定变化。造成这一波动现象的主要原因是由于钢绞线与夹片从锚具内侧拔脱时,由于锚具内外钢绞线的应变相差较大而发生应变重分布现象,千斤顶会产生一个瞬时滑移,由于惯性的影响,千斤顶的张拉力和位移也将经历从静平衡—动平衡—静平衡的过渡阶段,造成千斤顶的力值和位移测试结果在时程曲线的下限稳定值附近出现短暂的波动现象。所以,突变曲线段下限稳定值应以波动曲线之后达到另一稳定阶段初时刻的值为准。 图13 反张张拉力突变过渡阶段 本文中根据力学平衡和变形协调条件,推导了反张法检测单根钢绞线锚下张拉力的力学机理,并对其最大理论测试误差进行了深入分析,指出了该方法的适应条件。最后结合施工现场的最常用施工机具和设备,提出了一种非常实用的测试方法和系统组成,并在室内静载锚固试验机上进行了验证。主要研究结果如下: (1)本文中提出的反张法测试体外束张拉力的方法力学概念清晰,设备系统组成简单,试验规律具有可复现性,适用于任意锚固点间距大于16.26 m的体外预应力混凝土桥梁,基本满足锚固点间距大于9.76 m的体外预应力混凝土桥梁。 (2)夹片与锚具拔脱临界时刻不同参数曲线的敏感性,依次是力-位移曲线>力时程曲线>位移时程曲线,其中以力-位移曲线最为敏感,宜优先作为判断依据。 (3)体外束锚下有效张拉力应取主梁原有锚具与夹片拔脱临界时刻,突变段曲线下限稳定时刻的测力环测试结果。2 实验验证与试验参数

3 试验结果及夹片拔脱临界状态分析







4 试验结果分析与讨论
4.1 千斤顶夹持点与远端锚具之间钢绞线受力后长度L滑移稳定取值的合理性分析
4.2 夹片与锚具拔脱临界时刻不同参数曲线的敏感性分析
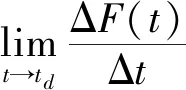
4.3 锚下有效张拉力大小的取值时刻分析
4.4 突变曲线下限附近波动现象分析
5 结论
——钢绞线的断束断丝的防治及发生时采取的措施

