燃烧室纵向压力振荡对燃料掺混过程的影响

汪广旭，刘占一，谭永华，陈建华，陈宏玉

(1.西安航天动力研究所 液体火箭发动机技术重点实验室，陕西 西安 710100；2.航天推进技术研究院，陕西 西安 710100)

0 引言

液体火箭发动机燃烧不稳定现象往往伴随着较高幅值的压力振荡，对发动机推力室、发生器等重要部组件可靠性构成了严重威胁。高频燃烧不稳定(high frequency combustion instability，HFCI)现象发生的一个重要依据是燃烧室内压力振荡的基本规律与燃烧室固有声学模态一致，其本质是热声耦合形成的共振现象[1-5]。HFCI现象的研究大体上包括激发机理和维持机理两个方面[6]，根据其激发过程的不同，可以将其分为两类：线性自发激励和非线性触发激励，前者在噪声量级的扰动情况下就可以逐渐增长为有限幅值振荡，也称绝对不稳定；后者需要一定幅值的外部激励才会激发燃烧室内周期性的振荡，也称条件不稳定。然而，对于现有的研究手段而言，针对HFCI现象瞬态激发过程的研究仍然面临很大挑战，通过仿真和实验揭示相应的激发机理亦存在很多的不确定性。

相比之下，维持机理的研究相对容易。这是因为，一般认为对于通过流动实现燃料掺混的燃烧室发生HFCI现象时，其内部燃料流动掺混、燃烧释热以及声振三者之间存在明显的耦合关系[7-8](见图1)。因此，采用解耦思想或方法，研究燃烧子过程与燃烧室压力振荡之间的相互作用过程，就能够揭示维持HFCI的关键内在机理，从而为降低实际发动机燃烧振荡幅值提供参考。宏观上，Rayleigh准则[9]给出了维持HFCI的必要条件，即当燃烧释热与压力振荡之间的相位小于90°时，压力振幅就可能会被放大。实际情况是，推进剂在发生化学反应之前都需要经历一段关键的掺混过程[10]，这一过程往往决定了下游燃烧过程的特征时间和特征位置，是决定最终热声耦合强弱的关键物理过程之一。由于上述掺混过程通常在靠近喷注器的区域完成，该区域也被称为声振敏感区[1-2]，研究该区域内燃烧室压力振荡对燃料掺混过程的影响对于揭示HFCI现象的维持机理具有重要意义。

图1 燃烧室流动、燃烧及声学之间的耦合关系Fig.1 The coupled relationship among flow, combustion and acoustics in combustor

相对于液态燃料的雾化燃烧，气态燃料的非预混燃烧过程更容易受到燃烧室压力振荡过程的影响[3]。Culick等人指出：气态燃料射流剪切掺混涡在初始状态具有最小能量量级，此时容易受到燃烧室压力振荡的影响[6]。Purdue大学近年来的研究也表明：喷嘴出口射流剪切涡不仅决定下游燃料的掺混过程，还与不稳定频率之间关系密切[11-14]。美国空军实验室(AFRL)的研究表明：喷嘴射流声振敏感性可以用燃料喷嘴出口射流的动能ρu2/2来衡量，当燃烧室压力振幅与该值的比值达到某一个值时会显著影响其下游的掺混过程[15]。为了进一步认识两者之间的相互作用规律与燃烧稳定性的内在联系，本文在上述工作的基础上，重点讨论了燃料射流剪切掺混过程与燃烧室内压力振荡的非定常作用过程，并结合相应工况下的轴向平均温度和燃烧释热分布，分析了上述过程与稳定性之间的关系。

1 模型及方法

1.1 模型及思路

本文的研究对象是一个内喷嘴长度可变的气/气同轴剪切单喷嘴模型燃烧室[12](continuously variable resonance combustor,CVRC)，详细结构如图2所示。

图2 CVRC燃烧室结构Fig.2 CVRC combustion chamber

图2中，不含喷嘴燃烧室长度约Lc=390 mm，燃烧室直径Dc=45 mm，氧喷嘴内径dio=20.5 mm，燃料喷嘴内径dfo=23 mm。氧化剂和燃料分别通过内、外喷嘴进入燃烧室，并通过氧喷嘴缩进段(长度10 mm)内的射流剪切过程实现掺混，氧化剂(57%水蒸气，43%氧气，初始温度1 030 K)流量0.32 kg/s，由90%浓度的过氧化氢分解得到；燃料(甲烷，初始温度280 K)流量0.027 kg/s。

Purdue大学针对此燃烧室自发激励燃烧不稳定现象开展了大量的实验，得到的一阶纵向频率信号功率谱密度PSD1st随氧喷嘴长度的变化曲线如图3所示[13-14]。可以看出，通过调节氧喷嘴长度Lpost，可以改变燃烧室内压力振荡幅值，当Lpost位于88.9 mm左右时，PSD1st低于25×10-5MPa2/Hz，烧室处于稳定状态；当Lpost位于139.7 mm左右时，燃烧室处于不稳定状态，从而为本文所研究内容提供了2个对比工况。本文首先对上述2种典型工况(Case I:Lpost=88.9 mm，Case II:Lpost=139.7 mm)进行仿真研究。

上述2个工况的稳定性差异是通过调节氧喷嘴长度，继而改变燃烧室声学特性来实现的，并没有改变内外喷嘴出口射流的动能，因此，可以用来讨论不同幅值压力振荡对燃料射流掺混过程的影响。为了单独对比不同射流条件与不稳定性之间的关系，本文增加了第3个工况，与第2个工况的唯一区别是，该工况通过人为降低氧喷嘴直径(Case III:dio=15.4 mm)来提高其出口射流动能，3个工况下喷嘴几何差异如图4所示。

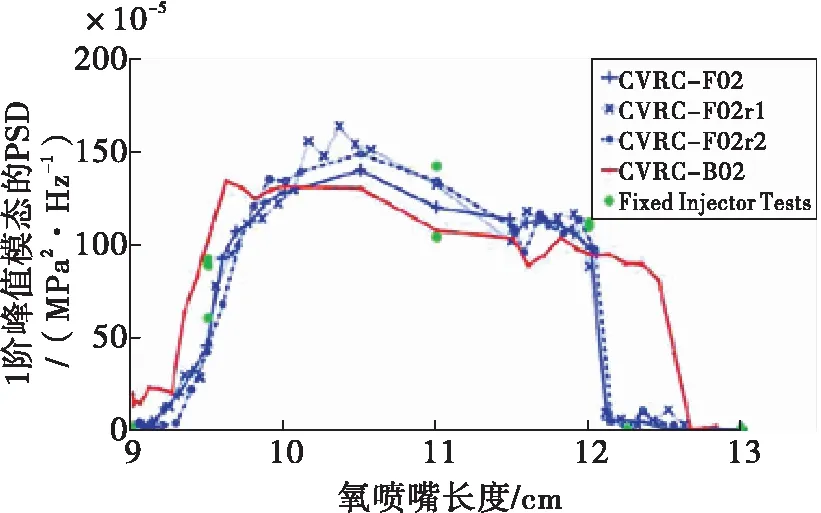
图3 功率谱密度随氧喷嘴长度的变化曲线Fig.3 PSD(Power Spectral Density) curve along with the length of oxgen nozzle

图4 喷嘴几何差异Fig.4 Differences of injector geometry

1.2 方法及验证

本文采用带化学反应的三维非定常脱体涡模拟方法(DES)[16-18]，其中湍流模型采用两方程的k-ω模型，为了减小计算量，采用一步总包的化学动力学模型如下

CH4+ 2O2→ 2H2O + CO2

燃烧模型采用有限速率模型，燃料喷嘴和氧化剂喷嘴均设置流量进口，且给定温度，在计算域出口，由于喉部的存在，出口达到超音速，采用压力外推边界。为了进一步降低三维非定常计算量，仿真采用周向1/12模型进行计算，其网格划分结果如图5所示，3种工况下结构化网格数量均达到了130万量级。

图5 计算网格Fig.5 Computational grid

为了更好地分析燃烧室压力脉动的空间分布情况，本文从氧化剂入口沿燃烧室轴线上每隔25 mm设置一个压力脉动采样点(SP)，共设置20个，分别编号SP01～SP20。为了便于后续的对比，各测点位置以喷注面作为参考，由于Case I的氧化剂喷嘴要短，故实际Case I的测点只有SP03～SP20。各工况下的采样点分布如图6所示，其中，采样点SP06靠近喷注出口，其采样结果可以代表喷注面处的压力脉动情况。

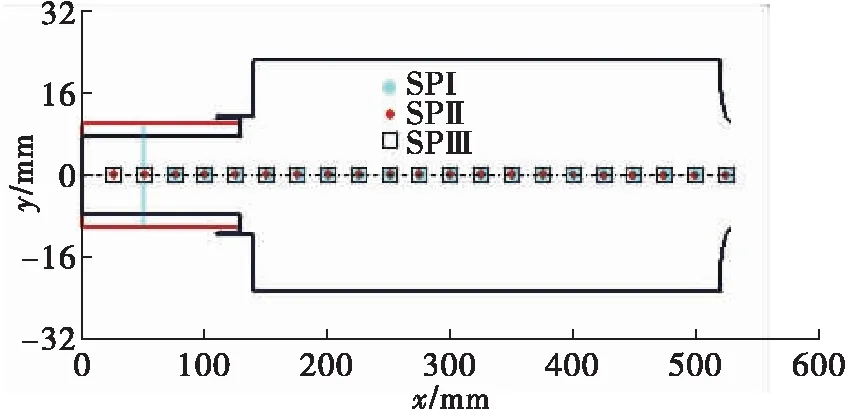
图6 采样点分布Fig.6 Distribition of sampling points

图7给出了Case II工况达到周期振荡状态后喷嘴出口测点SP06的压力脉动在7 ms时间内的仿真(红色实线)与实验对比结果(实验结果见参考文献[14])。可以看到，总体上仿真得到压力脉动峰—峰值与实验测量结果基本吻合，都在0.6 MPa附近。然而，相同时间内，仿真得到的主要信号周期数较多，意味着相应的振荡频率略高。为此，本文给出的解释是：①本文采用了一步总包的化学反应，仿真计算中燃烧产生的放热量偏高会造成局部声速偏大，进而引起振荡频率偏高；②仿真计算中未考虑实际燃烧室内壁面换热过程，后者会影响相应区域的局部温度，进而降低局部声速。燃料通过非定常射流剪切涡的掺混过程是本文研究的重点，这一阶段的气态燃料和氧化剂主要以单纯的流动过程为主，故在此前提下，忽略上述仿真误差对所研究内容的影响。

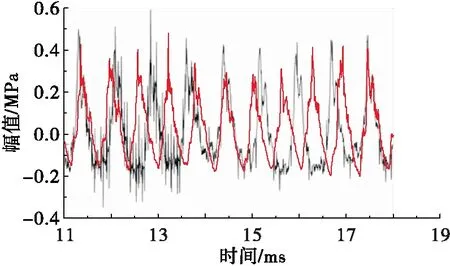
图7 采样点SP06压力脉动的实验对比结果Fig.7 Comparison of dynamic pressure between simulation and experiment at SP06

2 结果分析

2.1 燃烧室压力振荡的主要特征

图8直观地给出了3个工况下测点SP06的非定常压力脉动对比情况。从图8中可以看出，Case II的压力振荡幅值最大，稳定性最差；Case I的压力振荡幅值最小，且没有明显的周期性现象，稳定性最好；Case III的稳定性和压力振幅介于两者之间，具有明显的周期性振荡，但压力振荡幅值明显小于Case II。Case I和Case II的对比结果符合图1所示的实验规律，说明氧喷嘴长度对于改变燃烧室稳定性具有重要影响。Case II和Case III的对比结果说明，除了氧喷嘴长度影响稳定性以外，喷嘴射流动能的改变同样会对稳定性带来显著的影响。

一般认为，HFCI现象容易在燃烧室低阶声学模态上出现，此时，实际压力振荡幅值的空间分布(即振型)与相应的理论声模态接近。通常采用基于各向同性假设的波动方程来计算燃烧室声学模态，忽略了速度及温度梯度对燃烧室局部声速的影响，计算得到的声学模态与实际振型的误差较大。因此，获得燃烧室实际振型是分析HFCI现象的基础。图9给出了Case II工况各采样点压力脉动的频域结果，并分别用蓝色虚线和红色虚线标记了一阶、二阶声学振型的幅值分布结果。由于本文所研究的单喷嘴燃烧室的长径比较大，低阶纵向声学振型和横向振型的频率差距较远，因此，图中所示的一、二阶声学振型皆是纵向型的。

图8 各工况压力脉动的时域结果Fig.8 Pressure oscillation for different cases in time domain

图9 各测点压力脉动频域结果Fig.9 Pressure oscillation in spectral domain

取各工况一、二阶纵向振型对应的分频幅值(Case I是稳定的，其一、二阶分频幅值相对不太明显)可以得到实际的振型图，如图10所示。其中，相同工况的一、二阶振型采用同样的颜色表示，实线对应一阶，虚线对应二阶，并用青色虚线标记出了实际喷注面位置，绿色虚线标记出了一阶振型波节位置。从图中可以看出，对于Case II工况，除了进出口处，其一阶振型在喷注面及下游约80 mm位置处存在两个明显的波腹，该区域内压力振荡幅值相对较高，意味着该区域内压力振荡对流动过程的影响会比较显著。此外，由Case II的一阶振型可以看出，当HFCI发生时，实际燃烧室内的振型分布与理论声模态是存在很大差异的，对于本文所讨论的情况，后者的结果通常认为一阶振型或模态的波腹只存在于上下游边界处，而波腹与波节之间的幅值是线性变化的。

图10 实际的一、二阶纵向声学振型Fig.10 Real 1st and 2nd mode shape

从Case II中二阶振型分布情况看，氧喷嘴内部同样激发了明显的二阶纵向振型，其中存在2个明显与一阶振型空间正交(相位相反)的波节点，而相对地，这一趋势在燃烧室内并不是非常明显，相应二阶振型的幅值较低。以上结果意味着，对于此类喷嘴，当燃烧室内一阶纵向振型被激发时，其喷嘴内会先于燃烧室被激发出二阶纵向振型。Case III与Case II的上述趋势类似，唯一的区别是，Case III中，氧喷嘴内二阶振型波腹位置处的振幅与一阶振型波腹处的振幅之比要小很多。这说明，随着纵向不稳定性的提高，上述氧喷嘴二阶振型对应的能量也在不断提高。根据上述发现，实际工程中可以通过检测喷嘴内部的一、二阶纵向压力振荡的情况来判断燃烧室内是否激发了一阶纵向振型。

从Case III的结果可以看出，当前射流动能的变化量只能降低不稳定振荡的幅值，并没有从根本上改变模型燃烧室的稳定性。

2.2 燃烧室非定常压力振荡过程

从上述结果看，通过改变氧喷嘴长度和燃料射流掺混过程都会改变实际的热声耦合效果(即燃烧室压力振荡幅值的大小)。分析燃烧室非定常压力振荡过程对于揭示其维持机理具有重要意义，也是分析压力振荡对燃料射流过程影响的基础。以图11所示Case II工况采样点SP06的压力振荡过程为例，在1个主要周期内分别取5个典型时刻，1个波峰时刻、2个波谷时刻和上升、下降段振幅1/2处，得到图12所示3个工况下的燃烧室压力振荡过程，并分别用虚线和箭头给出了图10所示实际一阶纵向声学振型波腹、波节位置以及该时刻的波动方向。

图11 SP06测点压力振荡(Case II)Fig.11 Pressure oscillation of SP06 sampling point(Case II)

从图12中可以看到，各工况燃烧室内纵向压力波动强弱与其稳定性相互对应，稳定性最差的Case II工况振荡幅值较大，具体表现在为，T1时刻，压力波从边界开始反射，并向波腹位置对向传播；T2时刻，波腹位置处压力开始升高，直至T3时刻，2个方向的波在波腹位置处相遇，此时波腹附近的脉动压力幅值达到最大，在此之后，波腹处的脉动压力幅值开始衰减；T4时刻出现了两个反向传播的压力波，并在T5时刻传至边界附近，后者随之压力升高，如此循环往复。可以看出，上下游压力波并没有在喷注面处相遇，而是在下游约80 mm相遇，这是造成上述Case II中一阶振型在喷注面附近2个波腹的主要原因。另一方面，由于该区域是主要的燃烧释热区，根据Rayleigh准则，燃烧室内的压力波动过程因此得到了维持。显然，对于稳定的Case I工况，由于氧喷嘴长度较短，如果燃烧室内形成如Case II的波动过程，则上下游压力波相遇的地方要更靠下游，从而远离主要的燃烧释热区，造成波动过程不能得到维持。Case III的压力波动过程与Case II类似，但明显弱于后者。由于两者轴向长度相同，意味着上下游压力波相遇的位置相同，因此可以预见，出口射流动能最终改变的是主要燃烧释热区的位置或分布情况。因此，还需要对燃料非定常掺混过程进行深入分析。

图12 不同时刻压力振荡结果Fig.12 Pressure oscillation at different time

2.3 喷嘴非定常射流剪切过程

对于本文所讨论的气/气同轴剪切喷注形式，氧化剂和燃料通过射流剪切作用实现掺混，此过程中形成的涡的强弱一定程度上反映了掺混效率。由于喷注面附近既是声振波腹区，又靠近剪切涡形成的初始位置，因此，喷注面附近的涡量演化过程是非定常流动分析的主要对象。图13给出了Case II工况，喷嘴出口附近T1、T3、T5时刻对应的氧质量分数分布。可以看到，受T3时刻燃烧室压力振荡的影响，流动剪切形成的氧质量分数边界层变得更为陡峭。

图14分别给出了上述不同时刻各工况燃烧室内涡量场演化过程。从图中可以看出，不同稳定性工况下，喷嘴出口射流剪切涡量场也呈现出了显著差异，其中Case II中的涡量峰值明显高于Case I。此外，与上文描述的现象类似，T3时刻喷嘴出口附近的相干涡结构出现了剧烈的径向抖动现象，并在下游发生了聚积(见红色圆圈内)。相比之下，稳定工况Case I中内外射流剪切形成的相干涡沿径向的的分布区域较窄，主要沿流向发展，并在喷嘴下游迅速耗散。总结Case I和Case II对比结果可以得出：燃烧室纵向压力振荡会引起喷嘴出口流动剪切涡径向抖动加剧，其结果是会导致相干涡结构在下游的聚积。对于本文所讨论的气态燃料和氧化剂，这种聚积现象会导致掺混效率的提高，从而使主要的燃烧释热区更靠近喷注面。

从图14中还可以看出，Case III与Case II涡量场的区别在于：Case III中各时刻氧喷嘴缩进段内相干涡的径向分布范围较宽，且涡量峰值对应的涡元数较多，但沿轴向没有出现类似Case II中的聚积现象。由于涡量是速度的梯度，Case III中氧喷嘴速度的增加使内外射流的速度比提高，从而使相应的涡量增加，提高了掺混了效率。然而，一方面，由于氧喷嘴速度的增加会使涡元远离喷注面的速度加快；另一方面，根据流体力学原理[19-20]，当流体涡量较强时，惯性流动占主导，涡元的抗扰动能力较强，耗散较慢。在上述因素共同作用下，虽然Case III中的主要燃烧释热区会更靠近喷注面，但其长度也会被拉长，后者实际上降低了声振敏感区的燃烧释热量，从而弱化了燃烧室的热声耦合效应，提高了稳定性。

图13 不同时刻氧质量分数分布Fig.13 Field of O2 at different time

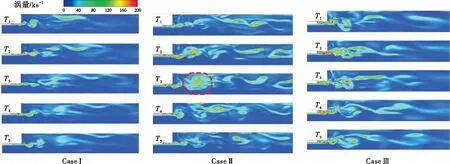
图14 不同时刻涡量场Fig.14 Field of vorticity at different time

2.4 轴向平均参数随稳定性的变化

针对压力振荡对射流过程的影响，上文从非定常的角度进行了分析，揭示了维持HFCI现象更深入的机理和细节。然而，考虑到工程实际中平均参数更容易获得，讨论上述非定常过程导致的燃烧室平均参数随稳定性的变化规律具有重要意义。图15、图16分别给出了3个工况轴线上平均温度和平均燃烧释热量的分布结果。从图15和图16中可以看出，Case II的高温区较其他2个工况更靠近喷嘴出口波腹位置；相对Case I，Case II的主要燃烧释热区更集中(集中在轴向位置0.18到0.3之间)，也更靠近波腹区；相对Case II，Case III的燃烧释热区较为分散(集中在轴向位置0.175～0.4之间)。基于以上对比结果可以得出：主要燃烧释热区集中程度和相对波腹的位置共同决定了燃烧室高频燃烧不稳定性，气/气同轴喷嘴出口动能的增加使燃烧释热沿轴向更加散布，有利于燃烧室稳定性的提高。

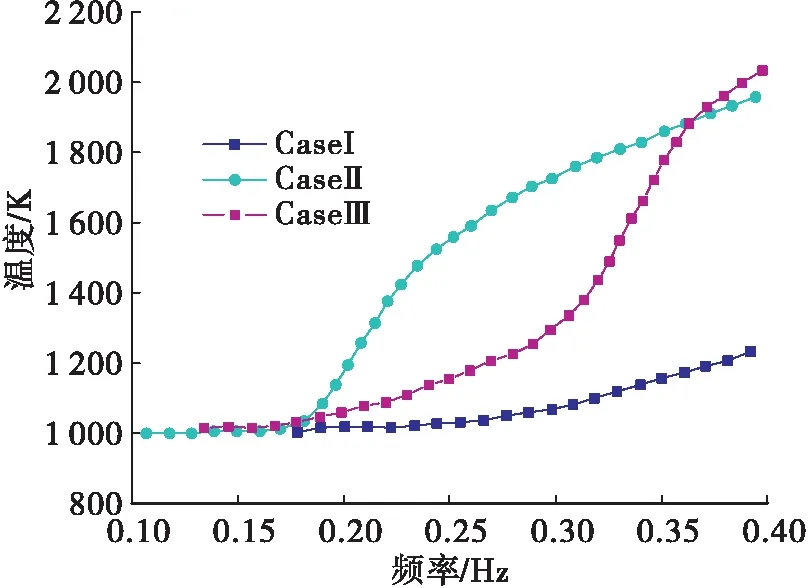
图15 沿轴线上平均温度分布Fig.15 Averaged temperature along axis

图16 沿轴线上平均释热量分布Fig.16 Averaged heat release along axis

3 结论

本文以气/气同轴剪切单喷嘴燃烧室为对象，在非定常燃烧流场仿真的基础上，分析了其纵向压力振荡过程，并采用解耦的思想讨论了纵向压力振荡对燃料射流掺混过程的影响规律，最终通过轴向平均温度和燃烧释热量的分布，讨论了上述影响过程与稳定性之间的相互关系。主要的结论有：

1)上下游压力波动在主要燃烧释热区相遇是维持纵向HFCI现象的必要条件，实际工程中可以通过检测喷嘴内部的一、二阶纵向压力振荡的情况来判断燃烧室内是否激发了一阶纵向振型。

2)纵向压力振荡能够明显强化燃料射流掺混过程，使主要燃烧释热区更靠近声振敏感区，后者反过来又会增强燃烧室内的热声耦合效应，使其稳定性降低。

3)纵向压力振荡对燃料射流掺混过程的作用决定了其下游主要燃烧释热区的集中程度和相对波腹位置，提高主要燃烧区的相对波腹位置或者使其更为散布时都会提高稳定性。

此外，本文还存在许多不足之处，针对所研究燃烧室更精细的全三维非定常燃烧流场仿真及相应的网格无关性验证还有待进一步探讨。