液体火箭发动机涡轮盘低周疲劳寿命预测

杜大华，王 珺，王红建，贺尔铭

(1.液体火箭发动机技术重点实验室，陕西 西安 710100；2.西北工业大学 航空学院，陕西 西安 710072)

0 引言

涡轮泵是泵压式液体火箭发动机的“心脏”，涡轮作为泵的动力输入端，其性能和可靠性直接影响发动机乃至火箭的运载能力与安全性。与航空、船舶、汽车及其他工业装备相比，火箭发动机涡轮热部件服役环境极端严苛，它不仅要承受较大的稳态机械载荷与热负荷，还要承受很大的力热冲击以及燃气腐蚀等。涡轮中高低温区相邻并存的大温度梯度、高比功率、高能量密度输出与气—热—固多学科耦合等因素，使得涡轮成为发动机中故障率最高的组件之一[1]。例如，VULCAIN—Ⅱ发动机氧泵一级涡轮盘出现了裂纹[2]，SSME的HPFTP涡轮叶片断裂[3]，CF—2F涡轮一级轮盘在试车中发生穿透性裂纹导致氧泵爆炸[4]，以及我国某型发动机涡轮盘在多次试车中出现异常振动、多处裂纹等。疲劳破坏是结构最主要的失效模式之一，涡轮盘出现的疲劳裂纹将影响发动机安全运行[5]。涡轮盘是发动机的核心部件，一旦失效，其后果往往是非包容性或灾难性的，而涡轮的可靠性决定了发动机的工作可靠性[6]。目前，涡轮设计已逐渐向大推质比、轻量化方向发展。由于结构强度、疲劳寿命引发的故障将对发动机的工作可靠性与安全性造成严重的威胁；同时，为满足多次启动、重复使用发动机的设计需求，需要对涡轮盘的服役寿命进行准确量化分析。

据统计，SSME涡轮叶片的开裂主要由高温蠕变与高速旋转离心力引起，且启动、关机瞬态效应对涡轮叶片的影响很大。科尔德什中心在进行涡轮泵结构热应力分析时，特别关注涡轮壳体和涡轮转子叶片的热应力状态，且认为涡轮寿命是一个多参数问题。由于结构、载荷的复杂性及大量的不确定性因素，进行动响应分析或动力学行为研究难度较大，因此本文仅开展在工作循环条件下涡轮盘的低周疲劳寿命分析。

目前，各航空大国都在发动机设计规范中明确了涡轮盘必须按照安全循环寿命进行设计，并积极开展涡轮盘低周疲劳试验，如P&W公司、R·R公司、美国IHPTET计划及俄罗斯航空发动机公司等建立了轮盘强度与寿命设计体系[7]。国内自上世纪70年代开始，以现役发动机定寿、延寿和在研发动机疲劳寿命设计工作为背景，开展了轮盘低周疲劳寿命研究[8]。

当前最常用的疲劳寿命预测方法有名义应力法、局部应力应变法和场强法等[9]。局部应力应变法是一种比较成熟的估算疲劳寿命的方法，相对于名义应力法精度高，但计算结果精度的稳定性较差。场强法是近年来发展较快并被广泛接受的一种计算疲劳寿命的方法，该方法认为疲劳寿命不仅与一点的应力状态有关，而且与缺口根部有限体积的整个应力状态相关。虽然场强法相对局部应力应变法预测的精度高，但计算工作量大。对于非比例加载—复杂多轴受力的低周疲劳问题，目前的分析方法主要有等效应变法、能量法和临界面法等[10]。对于火箭发动机涡轮结构，在高温多轴循环载荷作用下，应力应变状态复杂，尤其在非比例变幅交互循环载荷作用下，将材料单轴疲劳试验数据应用于多轴疲劳寿命预测，往往会产生较大的误差[11-12]。

至今，涡轮盘疲劳寿命研究工作主要集中在燃汽轮机与航空发动机等领域，对航天发动机涡轮盘的研究较少。已有的报道多是对涡轮进行稳态流场分析，对涡轮三维非定常黏性流动现象的研究很少，无法考虑发动机快速启动/关机瞬变过程力热冲击对轮盘寿命的影响，且一般采用材料单轴疲劳试验数据进行多轴疲劳寿命预测，从而导致寿命预测结果的准确性不高。

因此，本文通过对涡轮进行三维非定常全流场仿真，获取涡轮盘在启停阶段的力热冲击载荷及稳定运转过程中的稳态热力负荷；在此基础上，开展轮盘结构应力分析与材料疲劳性能试验研究；最后，进行多轴-单轴应力转换以将多轴低周疲劳转化为单轴疲劳问题，并基于局部应力应变法的M—C修正通用斜率方程对轮盘低周疲劳寿命进行预测，从而得到涡轮盘在工作循环下准确的寿命数据。

1 疲劳寿命预测理论

涡轮盘所承受的载荷十分严酷，结构局部区域接近或已进入屈服状态，本文采用安全寿命设计方法中的局部应力应变法进行低循环疲劳寿命预测，其中应力—应变寿命模型为基于M—C公式的修正通用斜率方程。整个分析流程如图1所示。

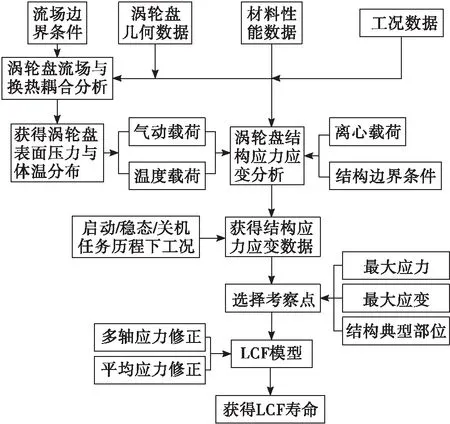
图1 涡轮盘低周疲劳寿命预测流程Fig.1 LCF life prediction process for turbine disk

由于缺乏材料的蠕变性能数据，暂不考虑蠕变的影响，通用M-C方程为

(1)

若利用材料的单向拉伸试验数据估算其相应的疲劳性能参数，可采用Manson通用斜率方程，即

(2)

式中：σb为材料拉伸强度极限；D为延性系数。可用材料拉伸断面收缩率ψ计算得到，D=-ln(1-ψ)。为进一步提高应变疲劳寿命预测精度，一般采用Muralidharan和Manson[13]基于50种材料疲劳性能提出的修正通用斜率方程

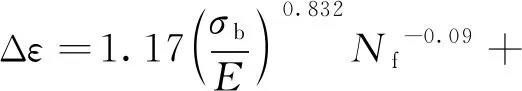
(3)

与式(1)和式(2)对比，式(3)不仅考虑了延性系数对塑性线的影响，还考虑了材料的拉伸强度极限对塑性线的影响，并加入了更多材料的疲劳性能数据，故修正的通用斜率方程比传统的通用斜率方程具有更高的预测精度。

由于材料应力应变与疲劳寿命关系式通常基于对称载荷疲劳试验结果，即M-C方程是在对称循环下获得，当结构承受非对称载荷时(应力比R≠-1)则要考虑平均载荷的影响[14]，需要对Δε-N曲线进行修正。采用Morrow弹性应力线性修正方法，则经平均应力修正后的通用斜率方程为

(4)

另外，涡轮盘关键部位常会经历显著的多轴应力场，由于材料疲劳性能试验数据是基于单轴应力或应变试验，因此需要进行多轴应力修正，将多轴应力等效为单轴应力，从而可以利用由材料试验获得的疲劳寿命曲线进行寿命估算。本文采用Von-Mises应力修正法和Manson-McKnight多轴应力方法[15]，在一次任务循环历程中对应力张量分量的变化范围进行修正，这样可以较安全地对涡轮盘的低周寿命进行预测。该方法是一种歪形能方法，多轴方法严格限制于比例加载，并假定材料为各向同性材料，则x、y、z三个正交方向上的平均应力和应力幅为

(5)

相应的剪应力为

(6)

由上述公式表示的平均应力为

(7)

其相应的应力幅为

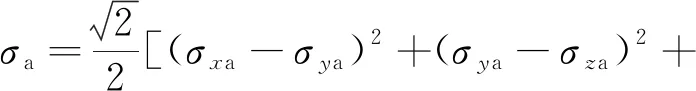
(8)

2 载荷预示

某型高压补燃发动机采用全进气反力式涡轮，结构如图2所示。扭转功率通过盘与轴连接花键传递，并通过4个螺钉将盘固定到传动轴上。由于涡轮具有形状复杂的流道、轮盘的高速旋转、表面的曲率效应以及常伴有的流动分离、二次流和尾迹等，这些因素不仅使得涡轮内部流场具有复杂的空间结构，同时在时间上表现为强的非定常特性。另外，涡轮启停时间短、气动载荷非定常特性显著。通过建立涡轮固体域与流体域模型，在考虑涡轮实际黏性气体非定常流动的基础上，选取湍流SST模型进行全三维非定常气—热—固耦合分析。

在多场耦合分析中设定涡轮入口流量边界条件，将计算得到的涡轮入口/出口燃气压力、温度值与试车测量数据进行对比，以检验分析结果的准确性。经对比分析，计算、试验涡轮入口/出口燃气压力、温度数据的一致性较好，从而验证了分析方法及所得载荷数据的有效性。

图2 涡轮结构示意Fig.2 The diagram of turbine structure

通过同时求解流体控制方程和固体热传导方程并平衡流固边界通量进行气热模拟，捕捉启停、稳定工作阶段涡轮内非定常流动现象，对涡轮盘启动、稳定运转及关机过程进行载荷预计，从而得到流场结构、温度分布，并得到轮盘静力学分析所需的气热载荷数据。

启动过程，因冲击时间很短，固体域温度变化的幅度要远小于燃气温度的变化。启动结束后，燃气参数达到稳定，但传热过程尚未结束，直至约45 s才进入传热的正规状况，在约150 s固体域的温度分布不再发生显著变化。关机过程，固体壁面温度下降速度较快，而内部温度下降较慢，因此关机结束时刻轮盘温度仍较高。

3 结构应力分析

3.1 涡轮盘有限元建模

涡轮盘有限元模型如图3所示。其中，盘轴螺钉连接采用考虑预紧力的螺栓连接。在试算的基础上，对关键部位网格加密处理，同时为了尽可能保证计算精度，进行了网格无关性验证。根据涡轮盘在工作时的实际力边界与位移边界定义模型的边界条件，约束盘轴连接花键齿接触面的周向以及轮毂端面轴向自由度。温度载荷和气动力通过涡轮非定常流场CFD分析与热传导分析获得，离心力载荷通过施加转速实现，以进行多场载荷作用下的静力学响应分析。

图3 涡轮盘结构有限元模型Fig.3 Finite element model of turbine disk

表1 稳态工况应力应变分析结果对比Tab.1 Comparison of stress and strain analysis results under steady state condition

3.2 稳定工作及启停过程静态响应

3.2.1 稳定工作阶段

稳定运行状态是轮盘一次任务工作时间最长的阶段，此过程结构传热已达到平衡，转速、气动载荷均达到稳定。分析图4及表1可得，最大等效弹性应变位置全部位于螺钉孔，这主要是在螺钉孔附近出现高的热应力和二次应力；离心力对轮盘等效应力的作用较大，且主要影响盘腹区域；气动力对盘等效应力的贡献相对较小，但对花键凹槽处的等效塑性应变影响较大；温度、离心力联合作用对轮盘变形影响较大，气动力对轮盘变形影响很小；同时，离心力、气动力共同作用对轮盘等效应力的影响并不是简单同向叠加。

图4 稳定工作过程应力、应变及变形情况(加载全部载荷)Fig.4 Stress, strain and deformation during stable operating (all loads)

3.2.2 启动过程

启动在4.0 s内完成，力热载荷迅速增大到额定工况。分析时将启动过程分为15个时间点，并忽略惯性效应，在每个时间点上进行准稳态静力学分析，以捕捉轮盘应力应变的变化情况。由图5可得，启动时等效弹性应变变化平稳，基本维持在0.005 9上下，而等效塑性应变在1.0 s点火至2.0 s在0.004 6附近，在2.0 s后快速增大，在4.0 s启动结束时刻达到0.031。另外分析应力应变云图发现，最大等效应力、最大等效弹性应变和最大等效塑性应变均出现在花键凹槽区域。与稳态工况相比，轮盘在启动较短时间内经历了复杂的应力应变历程，并在一定程度上表现出力热载荷共同作用下的冲击效应。

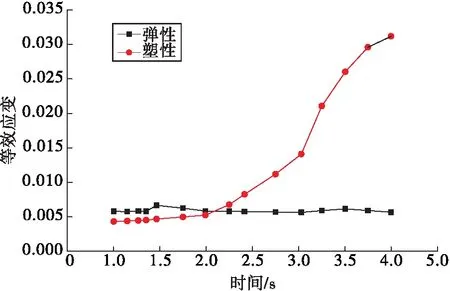
图5 启动过程应变变化情况Fig.5 Strain change history during startup

3.2.3 关机过程

在关机阶段，涡轮盘从额定工况迅速过渡到停机静止状态，转速、气动压力快速降为零，但结构体中温度变化缓慢(见图6)。

图6 关机过程应变变化历程Fig.6 Strain change history during shutdown

分析图6知，关机时等效塑性应变在0.4 s内快速达到平稳，并维持在0.013 5附近。分析应力应变云图发现，关机开始时最大等效应力在围带上，最大等效弹性应变在轮盘花键凹槽处，最大等效塑性应变则在螺钉孔处。随着轮盘转速持续减小，气动力和离心力也在逐渐减小，应力应变变化也逐渐趋于平稳。整个关机过程最大等效应力出现在关机开始时刻，说明了关机初始时刻对围带上应力幅值产生冲击效应。

4 材料疲劳性能试验

4.1 疲劳寿命分析依据

轮盘低周疲劳寿命是针对选定的危险点进行估算的，考察点的确定主要是基于在一次工作循环内各工况应力应变最大值位置以及轮盘典型部位进行选取的，选择P0～P9考察点，如图7所示。

图7 考察点设计Fig.7 Monitoring points design

分析图8得，轮盘螺钉孔附近P0、P8、P9点等效应力变化较大，花键凹槽处P2点的等效应力出现一个峰值。由图9可知，花键凹槽处P2点等效总应变的变化范围相对较大，而其它位置等效总应变变化范围相对较小。究其P2点在启动阶段出现上述现象的原因是，作用于涡轮叶片上的燃气具有启动压力峰，气动压力产生的扭矩作用在花键上产生剪应力，气动压力对花键凹槽处的等效塑性应变具有较大的影响。通过分析考察点数据得到寿命预测输入数据，并可为材料疲劳性能试验提供参考依据。

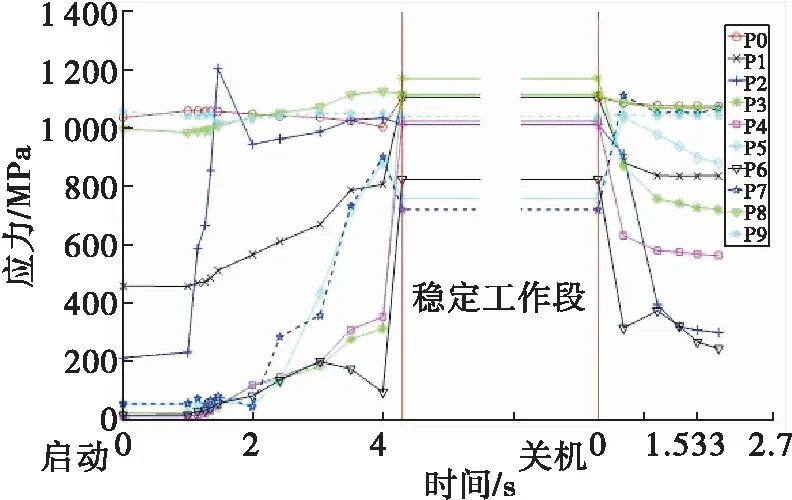
图8 考察点等效应力变化Fig.8 Equivalent stress change of the monitoring points

图9 考察点等效总应变变化Fig.9 Equivalent total strain change of the monitoring points

4.2 材料疲劳试验

虽然式(4)对大多数金属材料的应变疲劳均有较好的描述，然而与具体材料及其具体疲劳试验的符合程度或许存在一定的偏差，出现偏差的原因有多方面，其中主要有应力控制与应变控制疲劳试验之间的差异[16]，以及应力应变循环曲线受稳态情形的影响[17]。涡轮盘材料为GH4586，在相关材料手册中未收录其疲劳性能参数，另外低周疲劳寿命估算采用修正的通用斜率公式，其对GH4586描述是否准确，还需要经疲劳试验检验。因此，通过开展材料的疲劳试验研究，获得材料的疲劳性能，并利用试验数据修正斜率公式中相关参数，以提高对GH4586疲劳特性描述的精度。

试验采用轴力控制法，所需轴力根据最大应力(计算数据经换算后)确定。采用对称载荷加载方式，由于仿真结果是在复杂载荷条件下计算得到的多轴应力应变数据，需要对计算数据进行多轴—单轴应力转换。

采用“局部模拟法”开展标准试件寿命试验，试验采用P2点和P0点的应力应变数据，其中P2点为室温条件，P0点为410 ℃高温条件。常温、高温疲劳试验分别采用MTS—880疲劳试验机和带高温环境箱的QBG—50疲劳试验机，试验按相关标准[18-19]执行。室温试验有效试样共6个，高温试验有效试样共5个，如图10所示。

图10 疲劳试验件Fig.10 Fatigue test specimens

分析表2可知，高温下平均循环次数为5.658×105。同样，由表3可得，试验件在室温条件下的疲劳寿命分散度相对较小，试验件疲劳寿命对其平均值的最大分散度仅为22.4%，平均循环次数为290。

表2 GH4586材料高温疲劳试验结果Tab.2 Fatigue test results of GH4586 material in high temperature

表4 各考察点疲劳寿命预测值Tab.4 Fatigue life prediction value of the monitoring points

表3 GH4586材料室温疲劳试验结果

本文提出一种修改应变—寿命公式参数的方法，即按照寿命相等原则修正通用斜率公式(4)中的疲劳强度指数α和延性指数β，以得到新的疲劳寿命预估公式

(9)

式中：Δεas、Δεs分别为非对称、对称应变循环应变变化范围；σmas、σms分别为非对称、对称应变循环平均应力。

取常温下GH4586的σ0.2=1 430 MPa，E=226 GPa，ψ=30%。求解式(9)得α=-0.084，β=-0.475，给出常温下修正后的通用斜率公式为

(10)

5 疲劳寿命预测

基于应力应变分析结果，针对考察点利用修正后的通用斜率公式估算疲劳寿命，结果如表4所示。表4完整地给出了各考察点在低周疲劳寿命预测过程中的各主要参数。其中，“最大等效应力”和“最大等效应变”是通过有限元分析得到，“等效应变范围”和“σm-eq”分别是针对“最大等效应力”和“最大等效应变”，在一个完整的工作循环内，通过各工况应力应变分量经计算而获得的。

分析表4，涡轮盘最低疲劳寿命在花键凹槽处，室温下对应考察点P2的预测值是128。该位置处于轮盘与轴传递扭矩的关键区域，花键的几何尺寸效应、启动过程燃气压力峰对该区域疲劳寿命的影响较大。

6 结论

1)进行了涡轮盘载荷、应力分析及材料疲劳性能试验，得到涡轮盘低周疲劳寿命数据。

2)分别针对涡轮在启动、稳定工作与关机不同阶段气动力、离心力及温度载荷对涡轮盘应力应变及寿命的影响进行了分析，得到轮盘不同工作时间段、不同载荷对疲劳寿命的影响规律，轮盘启动力热冲击的影响最为显著。

3)轮盘低周疲劳寿命预测值与试验值基本吻合，证明了基于等寿命原理的多轴低周非比例加载下疲劳寿命预测模型的有效性。

4)在后续的研究中，需要考虑在流体压力波动、尾迹及机械振动等影响下轮盘的高周疲劳、高低周复合疲劳和蠕变特性等。