基于深度学习的飞行载荷测试与反演方法研究

金鑫，殷建业，王健志

(沈阳飞机设计研究所扬州协同创新研究院有限公司 技术部， 扬州 225000)

0 引 言

复合材料在飞机结构上的大量应用，带来了机体减重的同时也产生了一系列的安全性和可靠性问题。通过监测飞机的气动载荷可以获知飞机在服役过程中的过载和异常载荷状态，对飞机起落的安全性能进行评估，同时指导地面人员对出现异常载荷的机体进行维修和维护[1]。气动载荷的历史数据可以对结构设计及疲劳分析做出指导，实时的载荷监控增强了飞机的态势感知能力，可以对飞机的稳定性控制带来增益[2]。

目前飞机真实飞行环境下的载荷测量方法主要包括直接法和间接法两类，直接法主要通过在结构的关键位置布置力传感器来测量翼面上的载荷分布[3]。由于机翼结构复杂、内部空间有限，难以安装大量的取压管及压力传感器，因此直接载荷测量法很难在载荷试飞中使用，而多应用于风洞试验中。间接法则通过测量结构的应变、位移等物理量的变化来间接推知载荷的变化。由于飞行过程中的机翼位移难以测量，基于应变电桥的载荷测试方法在工程中更为常用。将应变片布置在机翼的关键位置组成应变桥路，测量在载荷作用下的应变变化，通过地面载荷标定试验建立的载荷方程反推出飞机所受的载荷大小[4]。应变法载荷测量技术成熟、计算简单，然而随着飞机速度和机动性的提高，机翼的结构和形状也趋于复杂，使用传统的应变法只能对整机的总载荷或少数剖面的载荷进行测试，难以反映翼面的载荷分布情况；同时通过多元回归方法拟合的载荷方程也存在着较大的误差[5]。随着数字孪生技术的发展，地面数字模型也需要对空中飞机的载荷情况进行实时求解和显示。然而传统的逆有限元等计算方法计算量大，耗时长，无法满足实时求解的要求。为了解决这一问题，使用数据驱动模型方法是一种合适的选择。通过大量的试验数据建立并训练代理模型，用代理模型来近似替代复杂的物理关系，最终实现实时的载荷求解。在众多代理模型中，人工神经网络是近年来常用的选择之一，陈志煌等[6]使用RBF神经网络对机械臂的抓持载荷进行了反演，并通过仿真进行了验证;郑敏等[7]通过仿真数据训练BP神经网络，并使用振动位移数据对转子系统的载荷进行了识别。在航空应用中，人工神经网络可以用于飞行器的载荷识别，如王珲玮[8]使用改进的BP神经网络对某导弹模型的飞行载荷进行了识别，使用速度、高度、迎角等飞行参数作为网络的输入，输出关键截面的内力；P.M.Trivailo等[9]使用了人工神经网络对F/A-18飞机的尾翼的疲劳载荷进行了预测，将尾翼上布置的19个应变片获取的应变数据作为网络输入，建立训练网络，获得了加载在尾翼上的单点载荷；S.B.Cooper等[10]使用一个双层前馈网络模型对翼肋结构上的静态载荷进行了预测，使用了15个应变传感器的数据作为网络输入，实现在翼肋上两个点的载荷大小输出；D.Wada等[11]使用光纤布拉格光栅(Fiber Bragg Grating,简称FBG)传感器通过神经网络的方法对大展弦比的机翼气动载荷进行了反演，将两根光纤各30个FBG传感器布置在了3.6 m长的机翼的前后翼梁上，在风洞中进行气动加载，以60个FBG传感器的应变以及8个襟翼的角度为输入，输出了机翼的展向剖面载荷分布以及机翼的迎角。以上研究利用神经网络的方法实现了较低误差的从应变到载荷的逆问题求解，但是网络输出的结果也多为单点载荷或单个剖面的几个点的载荷。对于具有非平直翼型的现代战机来说，单点或单个剖面的载荷并不能完整反映翼面的载荷分布。

本文提出基于深度前馈神经网络的数据驱动方法，通过深度学习建立并训练多层前馈神经网络作为代理模型，以高超声速飞机常用的三角翼面为例对载荷分布进行反演，并对反演结果进行验证。

1 基于深度前馈神经网络的载荷反演方法

随着对飞机速度和机动性要求的不断提高，战斗机从最初的平直翼布局逐渐发展为三角翼、双三角翼、梯形翼等复杂的机翼布局[12]，相应的气动载荷在翼面上的分布也更为复杂。某超声速飞行器的翼面在某种典型飞行工况下的翼面气动力分布如图1所示，图中彩色区域表征了载荷大小，从下到上递减。

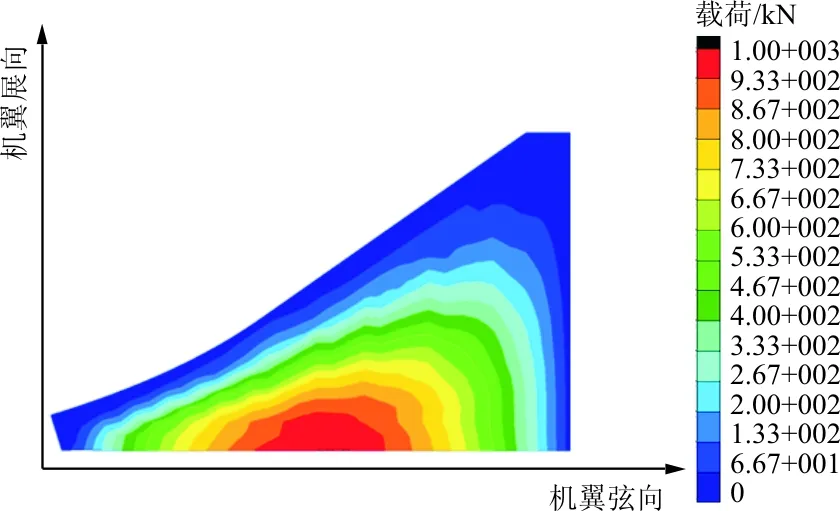
图1 某飞行器翼面载荷分布

从图1可以看出：翼面载荷最大值约在靠近机身的中部位置，且在展向和弦向分布都存在较大的变化。传统的飞行载荷测试方法测得的总载荷或剖面载荷并不能完整反映翼面上的载荷分布情况。对于机翼结构来说，载荷同应变的关系同其总体刚度矩阵相关，如式(1)所示。

F=Kε

(1)

式中：F为载荷矩阵；ε为应变矩阵；K为刚度矩阵。

由于机翼结构中有翼梁、翼肋等复杂结构，总体刚度矩阵很难求得。在工程应用中，当实际问题计算量很大、不容易求解时，可以使用计算量较小、求解迅速的简化模型来替代原模型。

人工神经网络是一种常用的代理模型，可以解决分类、回归、预测等多种问题，训练完成的神经网络可以实现输入到输出的快速计算，满足实时性的要求[13]。在众多的人工神经网络结构中，前馈神经网络适用于回归和函数拟合。前馈神经网络是一种层与层顺序连接的网络，包括了输入层，一个或多个隐含层以及输出层，其基本结构如图2所示。

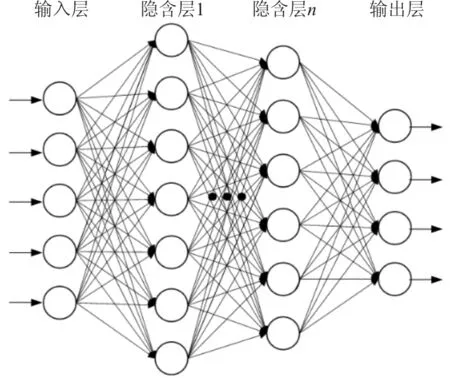
图2 前馈神经网络结构[14]

理论上讲，包含单隐含层的三层前馈网络可以解决任意复杂函数的拟合问题。然而随着需要拟合参数的增加，单隐层网络中神经元的规模呈指数扩大，复杂模型的训练效率随着参数的增加迅速降低。虽然具有单隐层的前馈网络足以表征任何函数，但是受限于网络规模无法实现。在更多的情形下，使用更多层的网络，即更深的模型能够明显减少神经元的数量，同时也能减少泛化误差[15]。

然而对于深度网络，在训练过程中使用的误差反向传播算法会使梯度传播逐渐变小，导致浅层的隐含层神经元权值得不到更新，出现了所谓的“梯度消失”问题。为此有研究者提出使用整流线性单元(Rectified Linear Unit，简称ReLU)代替传统神经网络中常用的Sigmoid单元构建前馈网络。ReLU单元易于优化，其处于激活状态时导数为1，梯度大且一致。但是其输入值小于0时，输出值恒定为0造成了其不能通过梯度方法学习那些使其激活为0的样本，存在死区。泄漏整流单元(Leaky-ReLU)是为了改进ReLU单元的死区特性而发展出来的一种非线性单元，其表达式如式(2)所示[15]：

f(z)=max (0,z)+a·min (0,z)

(2)

式中：z为单元的输入；a为一个小于1的常数；f(z)为单元的输出。

Leak-ReLU函数不同于ReLU，在输入小于0的情况下输出是一个较小斜率不为0的值，避免了输入小于0时输出为0的问题，更适用于拟合计算。为此本文构建以Leaky-ReLU为激活函数的多层前馈网络作为代理模型，对载荷反演问题进行求解。

2 有限元建模及计算

2.1 机翼有限元模型

本文采用高超声速飞机常用的三角翼作为研究对象，其外形及内部梁肋分布如图3所示，机翼结构均采用钛合金材料。

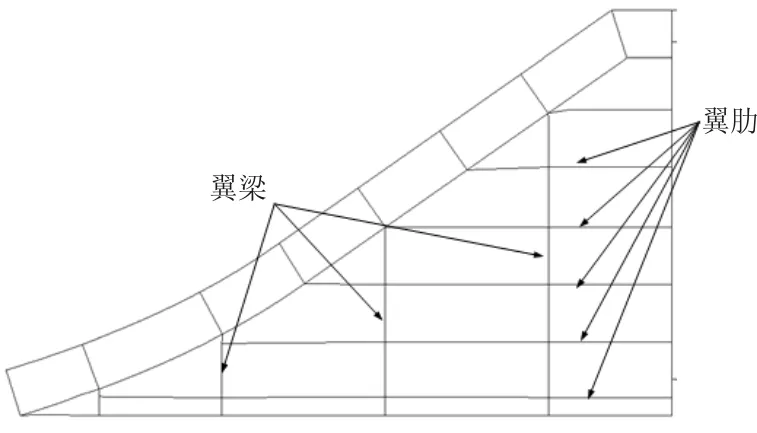
图3 机翼外形示意图

机翼使用SHELL单元建模，单元尺寸大小约为15 mm。为减小约束对计算结果的影响，同时建立机身模型，约束施加在机身对称面上，在机翼下蒙皮选择均匀分布的433个节点施加集中载荷，用于模拟气动载荷。

为了生成足够数量的样本用以神经网络训练和测试，需要构建同真实工况接近的多种载荷分布情况。通过将机翼分为前端、中部及后缘三个部分，分别在正弦函数的基础上通过随机参数化的方法生成如图4(a)所示的三条曲线，在机翼面上进行二维插值拟合，最终得到一组翼面的气动载荷分布，如图4(b)所示。通过随机生成三条曲线的分布参数，得到了5 000组翼面载荷分布，在所有分布中的最大载荷小于1 000 N，最小载荷大于-100 N。

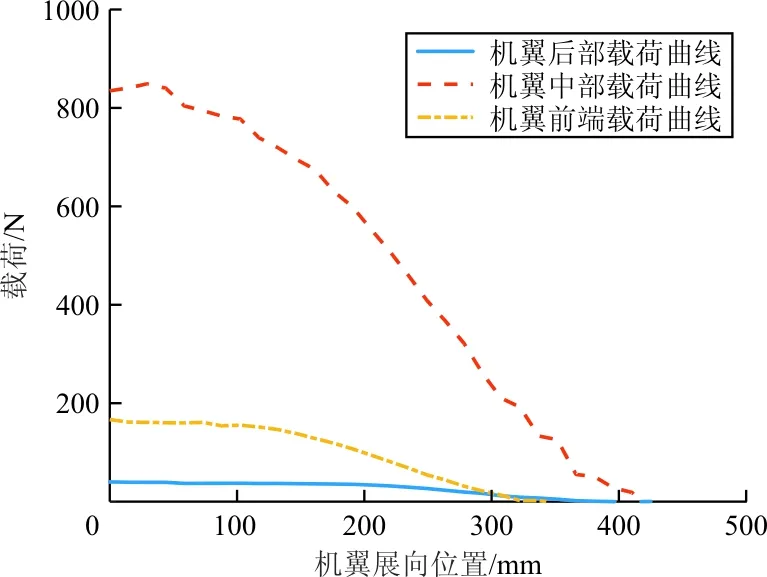
(a) 随机生成载荷曲线

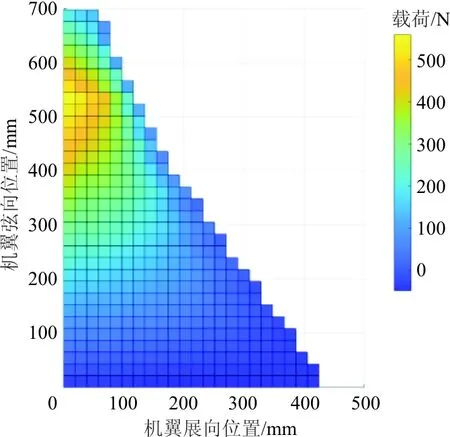
(b) 翼面载荷分布

2.2 应变测点位置选取

受限于机翼结构的复杂性，在真实的机翼结构上无法大量布置传感器，需要在机翼上选取少量合适的应变测点位置。考虑到机翼类似悬臂梁的结构，翼稍到翼根处的应变应逐渐增大，对于复杂的三角翼结构来说，机翼弦向和展向不同位置的应变对载荷的灵敏度也是不同的，为了对翼面上的应变载荷灵敏度进行评估，使用5 000组生成的随机载荷通过Nastran软件计算机翼展向的应变分布，并求得5 000组应变分布的方差如图5所示。

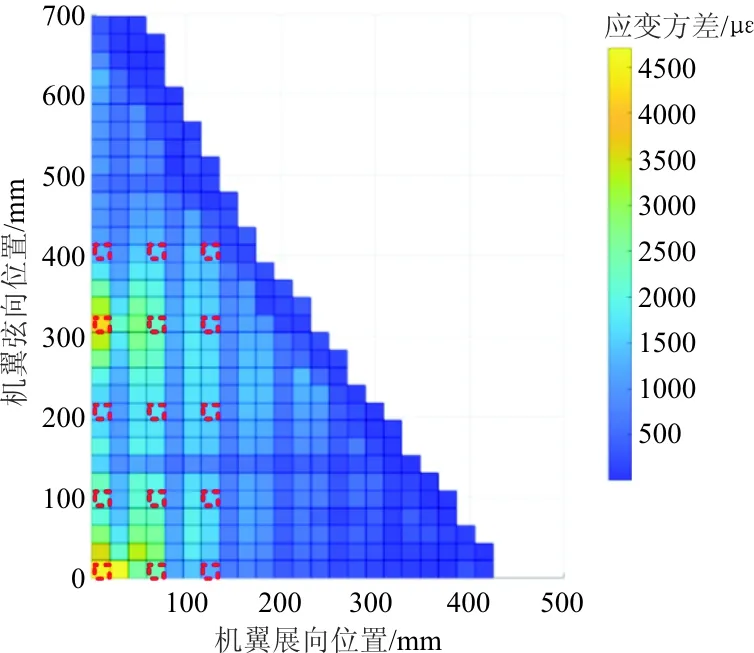
图5 翼面应变方差分布

从图5可以看出：机翼根部同机身连接处有两个方差较大的区域，意味着在载荷变化的情况下这些位置的应变变化也相应较大，为应变-载荷灵敏度高的位置。以此为依据并尽可能覆盖较大的翼面范围，选取了翼面上的15个测点提取应变数据，如图5中虚线框出的位置所示。

3 前馈神经网络构建及训练

构建神经网络结构首先需要分析网络的输入与输出。对于本文中的问题，输入为15个应变数据，而输出则是整个翼面433点的载荷大小。为了保留应变测点在翼面上的空间位置信息，将输入数据从15个点扩充为433个点，未采样位置的应变设置为0。构建的深度前馈神经网络如图6所示。

神经网络输入层为翼面应变逐行展开得到1×433大小的矢量，中间为四层全连接层，每层都采用Leaky-ReLU函数激活并加入批量标准化(Batch Normalization)层用以将样本分布归一化保证收敛速度。第一层全连接层输出大小为433，输入数据在同维度下进行仿射变换，将少量的应变点信息扩充至整个翼面；后两层全连接层输出大小为866，使数据在高维展开，得到更好的非线性拟合能力；最后一层全连接层为433大小的输出，对应翼面的载荷分布。

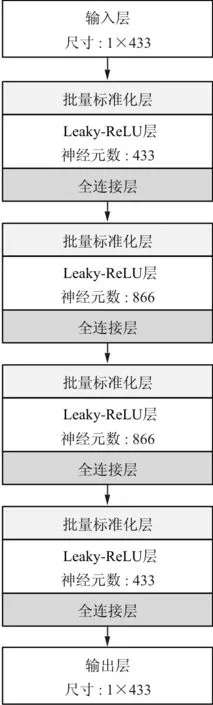
图6 深度前馈神经网络连接示意图

网络训练采用自适应矩估计(Adaptive Moment Estimation，简称Adam)优化方法，Adam是深度学习中新兴的一种优化方法，可以替代传统的随机梯度下降(Stochastic Gradient Descent，简称SGD)方法[16]。相较于SGD方法，Adam所需内存小，计算效率高，适合解决大规模的数据和参数优化问题。使用90%的样本进行训练，剩余样本做为交叉验证，即4 500个样本用于训练，500个样本用于验证。为了降低训练陷入局部极小的概率，使用小批量(Mini-batch)训练方法，批量大小为32，训练轮数为50轮，初始学习率设定为0.001，损失函数采用均方根误差(Root-mean-square Error，简称RMSE)。训练在本地计算机上进行，CPU为AMD Ryzen 5 4600U，6核心12线程，主频最高3.9 GHz。训练总耗时12分10秒。

4 载荷反演结果及分析

神经网络训练完成后，使用500个样本对其进行验证。在与训练相同的计算机硬件平台上求解500个样本耗时0.48 s，平均每次求解0.001 s，实现了实时的载荷分布输出。神经网络输出结果同验证目标的载荷分布平均误差约为最大载荷的5%，验证集中随机的一组载荷分布结果如图7所示。

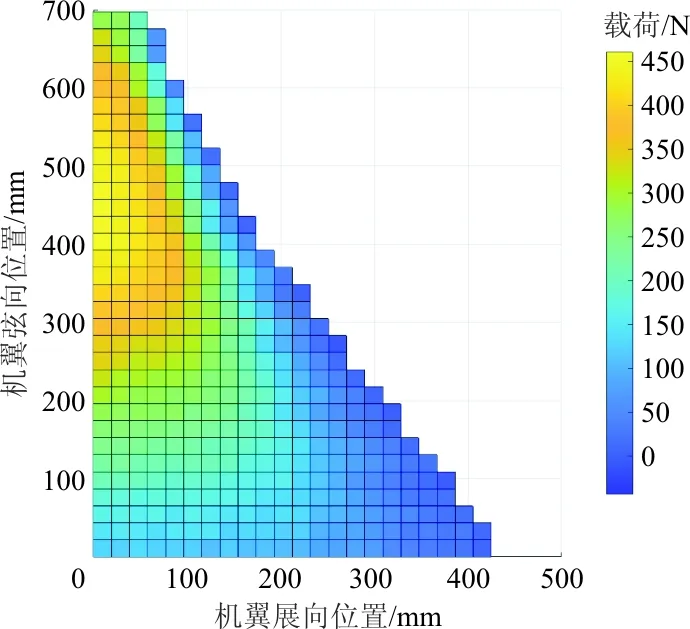
(a) 神经网络计算载荷分布

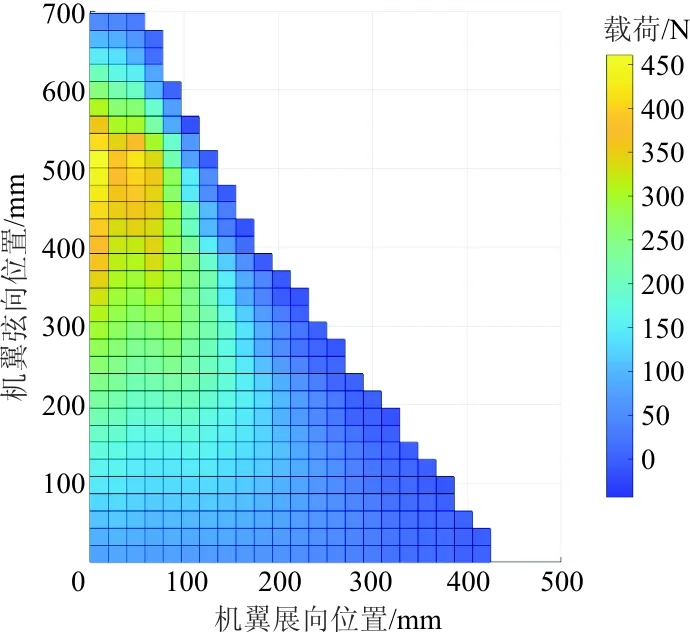
(b) 目标载荷分布

从图7可以看出：神经网络输出的载荷分布结果同验证目标的载荷分布接近。为了评估结果，对翼面上的总载荷和总压心进行求取，载荷分布样本的总载荷大小及总压心位置如表1所示。

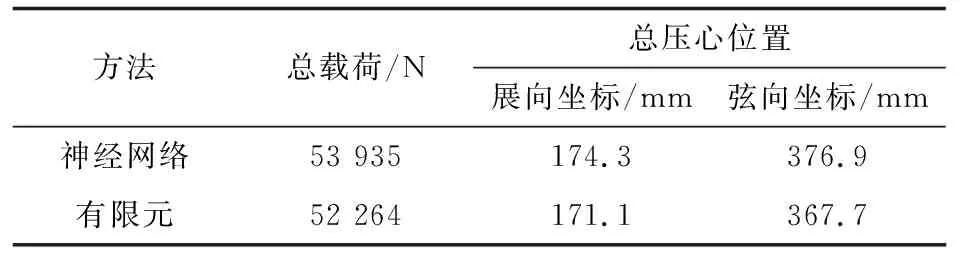
表1 总载荷及总压心计算结果对比

从表1可以看出：神经网络输出的载荷分布同目标载荷分布的压心距离接近。对500组验证结果的总载荷进行求取，得到总载荷的平均误差为0.2%，压心位置的平均误差为1%。除了总压心和总载荷之外，飞行载荷测试还关注机翼展向的剪力、弯矩及扭矩分布，对一组神经网络输出载荷和验证目标载荷进行计算，得到剪力、弯矩及扭矩曲线如图8所示。

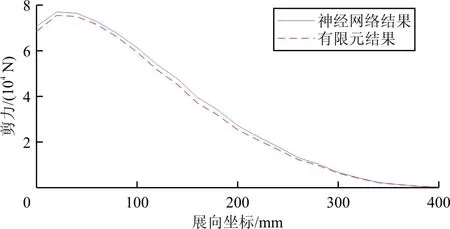
(a) 剪力分布对比

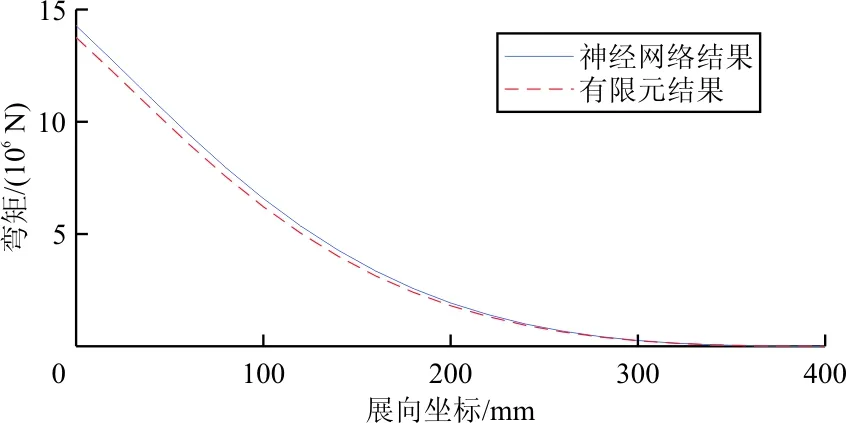
(b) 弯矩分布对比

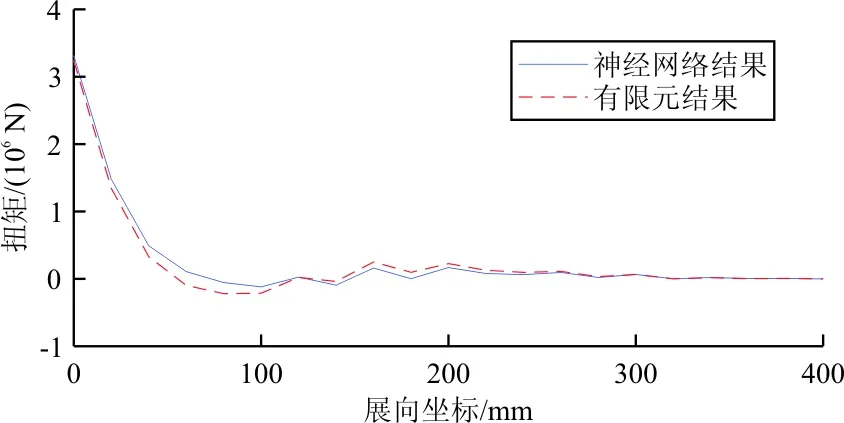
(c) 扭矩分布对比

从图8可以看出：神经网络输出的结果同目标结果接近，对500组验证数据的误差进行对比，剪力平均误差为0.6%，弯矩平均误差为0.4%，扭矩平均误差为8%。

5 结 论

(1) 基于深度学习的飞行载荷测试反演方法通过构建深度前馈网络作为代理模型，从机翼上少量的应变采样点反演得到整个翼面的载荷分布，改进了传统飞行载荷测试方法，实现了载荷分布的实时计算。

(2) 通过构建典型工况下的载荷分布建立训练样本集，对网络进行了训练及测试。通过交叉检验验证了代理模型的有效性，验证总载荷的平均误差约为0.2%，压心位置误差约为1%。

(3) 基于深度学习的飞行载荷测试反演方法实现了高精度的载荷测试，获得了更详细的载荷分布信息，为飞机结构设计及优化提供了指导，也为数字孪生技术的发展提供了技术支撑。