基于冲量定理的高速空投假人最大动载计算模型研究

程炜，杨春信，柯鹏，马坤昌，高春鹏，戚晓玲

(1.北京航空航天大学 航空科学与工程学院， 北京 100191)(2.北京航空航天大学 交通科学与工程学院， 北京 100191)(3.航空工业航宇救生装备有限公司， 襄阳 441003)(4.航空防护救生技术航空科技重点实验室，襄阳 441003)

0 引 言

救生伞是弹射救生系统的关键装备之一，国军标GJB 232-87要求，开伞过程中人体脊柱所受冲击力不应超过该标准的耐受界限[1]。目前工程上对开伞动载的评定以风洞实验和空投试验为主。风洞实验可测物理量更多，但受约束较多，无法真实还原降落伞实际工作状态，且更偏向于对伞气动特性和伞衣结构的研究[2-4]。空投试验更能真实反映系统的工作状态，但对于假人高速空投问题，由于假人复杂的气动外形使得开伞时刻的姿态差异巨大，导致动载测量结果波动复杂，试验结果的重复性很差[5-6]。此外，高速空投试验的成本高，考虑到飞机和天气的因素，其试验条件也很难完全重复。

相比于实验，理论分析和数值模拟能够快速地预测和检验不同设计参数或环境参数对开伞动载的影响，可以为系统设计的评估和优化提供重要的理论依据，对于提高系统设计水平、减少试验次数、节省设计费用和保障系统安全都有重要意义。

假人最大动载一般出现在救生伞充气过程中，因此充气过程中伞衣阻力特征是关键。理论研究通常将假人视作质点或刚体，救生伞采用充气距离或者充气时间模型，给定伞衣无量纲阻力面积变化规律，通过动力学计算确定开伞动载，例如，W.P.Ludtke[7]给出了系统水平运动下无量纲开伞动载；K.F.Doherr[8]将W.P.Ludtke的工作拓展到任意轨迹角的情况；王利荣[9]给出另一种确定最大动载的经验方法，最大开伞动载为充满瞬间伞衣阻力的两倍，并给出了物伞系统垂直下降时的最大开伞动载计算式；J.Potvin[10]提出基于冲量定理来分析开伞动载，并推广至多种空投条件，包括定点空投[11]、无收口降落伞[12]、伞群空投[13]以及回收物有火箭驱动[14]等，给出了系统在水平和竖直运动下开伞动载的计算式[15]，但是模型参数的确定比较困难。

基于冲量定理的开伞动载计算方法不依赖于伞充气规律的解析表达式或假设，适用于不同伞衣类型，有明确物理内涵、封闭的表达式，能快速确定关键参数影响，具有较好工程应用价值。

为此，本文在J.Potvin工作基础上，建立适用于高速空投情况的假人最大动载计算模型，根据伞系统拉直速度、充气时间、速度损失因子和动载变化因子计算特定空投条件下假人的最大动载，并通过算例在某特定空投系统中进行仿真，确定模型参数。

1 假人高速空投全过程描述

整个空投试验物理过程复杂，根据作用物体及其受力特点将整个过程分为3个阶段进行分析。在时间轴上描述空投试验过程中的关键点和关键阶段，如图1所示，空投过程包括：

(1) 自由坠落阶段(出舱阶段)AB，在A时刻释放假人，假人和伞包固定在一起自由坠落，只受重力和气动力的作用；

(2) 拉直阶段BC，在时刻B伞包打开，引导伞开始工作，并逐渐将伞系统从伞包中拉出，直至伞系统拉直，本试验采用的是先拉伞绳法，此过程中假人受到气动阻力、重力以及吊带的拉力的作用；

(3) 充气阶段CD，在时刻C伞系统拉直，伞衣开始充气，此过程中空气阻力极具增加，假人最大动载即发生在充气阶段。而后伞衣充满，系统稳定下降。

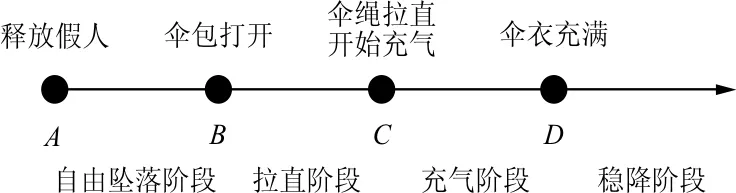
图1 假人高速空投物理过程

根据工程经验，动载峰值一般发生在CD段，即充气阶段。为此，本文针对充气阶段提出一种基于冲量定理的假人最大动载计算模型。

2 基于冲量定理的假人最大动载计算模型

2.1 假人最大肩带合力计算模型

对于假人，充气时间内在轨迹方向上冲量等于开伞前后的轨迹方向上的动量变化，则：

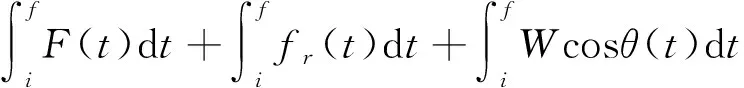
(1)

式中：m为假人质量；Vf,Vi分别为充气阶段结束和开始时刻的系统速度；F,fr分别为假人所受的肩带合力和气动力；W为假人所受重力；θ(t)为运动过程中系统轨迹角，系统水平运动和竖直运动分别对应于90°、0°。

对于高速空投，由于水平方向速度远大于竖直分量，且充气时间短，在此阶段内系统可视为水平运动，即θ=90°。另外，肩带合力远大于假人所受气动阻力，忽略重力和假人气动力冲量，有：

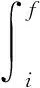
(2)

为了给出最大肩带合力，引入无量纲因子IF：

(3)

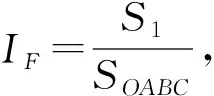
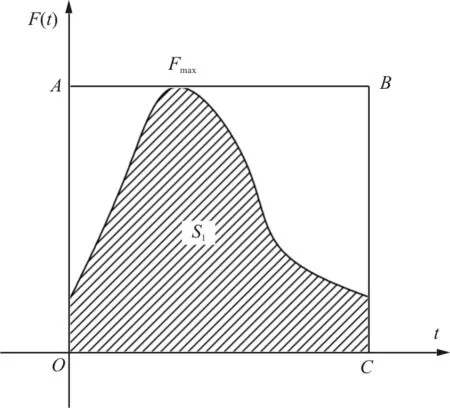
图2 IF物理含义

由于肩带合力为负值，式(2)可简化为

mVi-mVf=FmaxtmIF

(4)

式中：tm为充气时间。

由式(3)～式(4)可得：

(5)

2.2 假人最大动载计算模型

对于假人高速空投，根据国军标GJB 232-87，在救生伞设计中应关注开伞过程中人体脊柱对开伞冲击力的耐受强度(如图3所示)，假人动载表征假人在Zr轴方向上的力[1]。

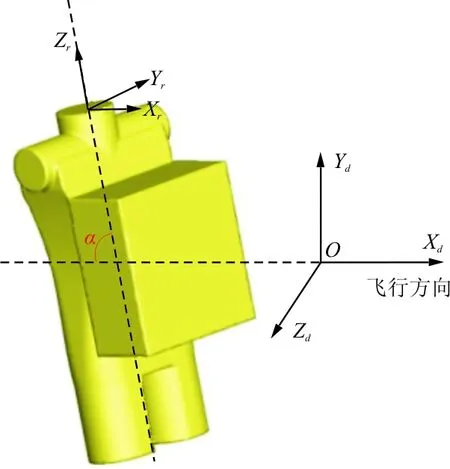
图3 假人坐标系示意图

定义假人姿态角为大地坐标系-Xd与假人+Zr轴夹角为α，由于充气过程中肩带合力可视为-Xd方向，因此姿态角α也为肩带合力与+Zr夹角。充气过程中Zr轴受力达到最大值FZmax的瞬间，有：

FZmax=Fmcosαm

(6)

式中：Fm为此刻的肩带合力；αm为此刻假人的姿态。

(7)

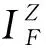
(8)

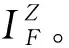
对于充满速度Vf，文献[15]分析低速情况下可以直接用系统稳降速度计算：

(9)

式中：W为伞物系统质量；(CA)d为稳降时的伞衣阻力特征。

对于假人救生伞高速空投，稳降速度和充满速度相差很大。由于拉直速度Vi为充气时刻初速度更容易获取，应用更加方便，因此定义速度损失因子η：

Vf=Vi-ηVi

(10)

η衡量了充气前后的速度损失效应。由此可以得到假人最大动载计算模型为

(11)

式(11)中充气时间tm由试验录像分析或计算中的特定充气模型决定。

图4 冲量定理模型应用思路

3 动载计算模型的应用

针对某特定空投系统，算例采用特定状态点的多体动力学仿真作为基础数据。算例中计算假人初始姿态角和转速均为零，称为零零姿态。

3.1 开伞过程的多体动力学建模

假人自释放至伞衣充满依次经历自由坠落(出舱)、降落伞拉直及伞衣充气三个阶段，本文动力学建模基于文献[16]的模型和方法展开，建立了拉直阶段质点弹簧模型和开伞阶段假人-救生伞系统两刚体动力学仿真模型。此外，拉直速度的计算则参考了文献[17]的结果，采用匀减速过程模拟空投起始到开始拉直的自由落体过程。

拉直阶段动力学仿真模型如图5所示，采用先拉伞绳法，将伞物系统处理为由若干个阻尼弹簧相连的集中质量结点。

图5 拉直阶段仿真模型

充气阶段的动力学仿真模型如图6所示，伞和假人均为刚体，伞气动力采用充气时间法[9]给出。

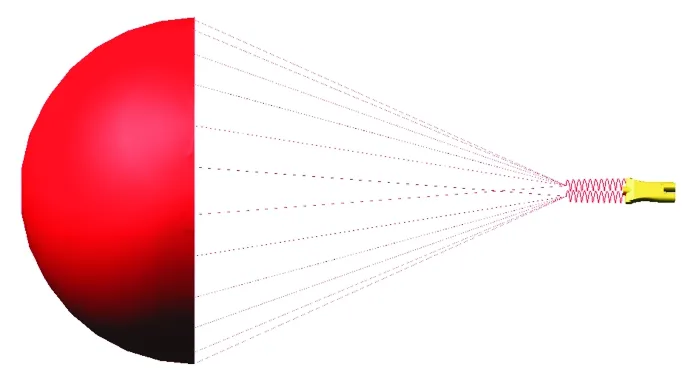
图6 充气阶段仿真模型

假人气动系数通过CFD获得[16]。

3.2 计算参数及工况

3.2.1 仿真参数

拉直计算采用的救生伞各部分质量及长度参数如图7所示。

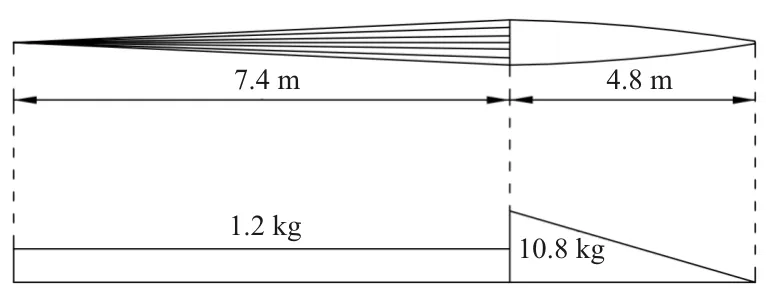
图7 伞衣伞绳质量及长度

引导伞拉力计算公式如下：

(12)

式中：Vys为引导伞速度；Ays为引导伞面积，本文取0.78 m2；Cys为引导伞阻力系数，本文取0.75。

本文采用充气时间法[9]模拟充气过程中气动阻力变化。试验确定的伞衣阻力特征曲线如图8所示。

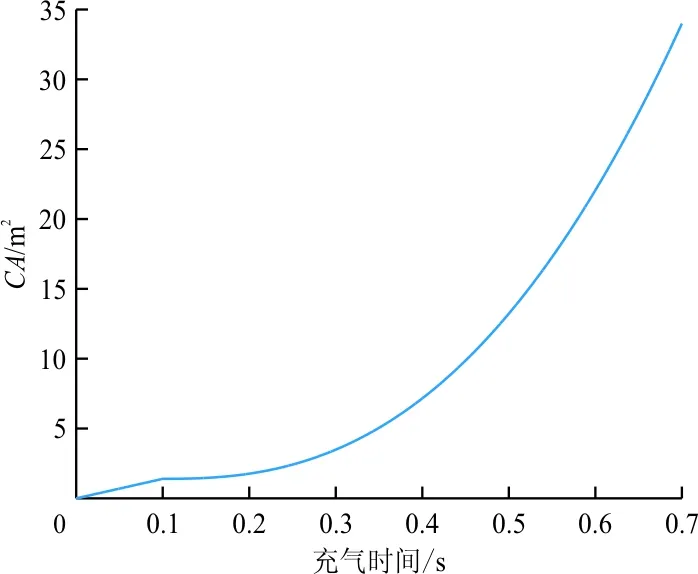
图8 伞衣阻力特征

充气过程中附加质量mf的计算为

mf=kfρ(CA)3/2

(13)

式中：ρ为空气密度；kf为附加质量系数，取0.41。

3.2.2 假人质量及空投速度

根据工程经验，假人动载对空投速度更敏感，在假人质量范围75 kg≤m≤150 kg内取4个点；空投速度范围缩小并取密，重点考察590 km/h≤v≤660 km/h，取8个点，共计32个工况点。工况点如图9所示。

图9 仿真工况点示意图

为了验证本文模型的有效性，取矩形内部任意4个点作为最大动载计算模型的预测点，其余28个点作为确定模型参数的基础状态点。

3.3 多体动力学仿真结果及分析

对工况在4 km空投高度下模型进行计算，不同质量下的假人最大动载关于空投速度的变化曲线如图10所示，可以看出：随着空投速度的增大，假人最大动载整体上也随之增大，同一速度下假人最大动载也是关于质量正相关的。个别工况点未表现出最大动载与速度的正单调关系，可能原因在于仿真对充气过程模拟的局限性上。

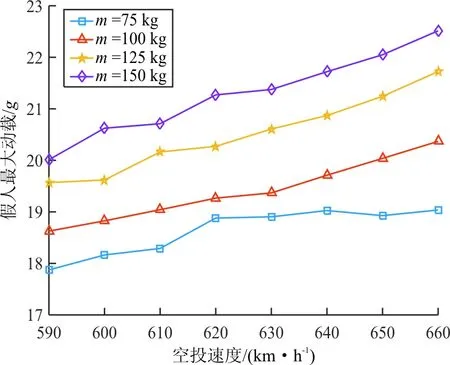
图10 最大动载关于空投速度变化曲线

图8所示的伞衣阻力特性规律是在来流方向始终与伞轴线方向一致的情况下得到的，在实际运动中，由于救生伞有姿态波动，来流速度并不一定始终与轴线同向，甚至可能出现瞬时速度与轴线垂直的情况，此瞬间充气过程将中断。本仿真基于图8所示的伞衣阻力特性规律，并未考虑以上几点。

3.4 冲量定理动载计算模型参数确定

3.4.1 速度损失因子η

根据仿真结果，在本工况下η大约取值为66.67%～75%，具体值与空投质量相关。为了获取不同质量下的η值，采用如下假设：对于同一具伞，在充气过程中系统损失的动能一致，则假人质量越大，其速度损失越小，即充满时刻速度应越大，即速度损失因子关于质量呈负相关，因此可以对质量、速度损失因子(如表1所示)作线性插值得到不同质量下速度损失因子η。

表1 不同质量下的速度损失

为了统一量纲，引入无量纲质量ε，

(14)

由式(14)可知，0≤ε≤1，取值0和1分别对应最小质量75 kg和最大质量150 kg。η的线性插值结果为

(15)

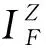
(16)

式中：下标i为第i个基础状态点结果；δ为所有工况点下本文模型与仿真基础数据的相对误差和。

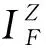
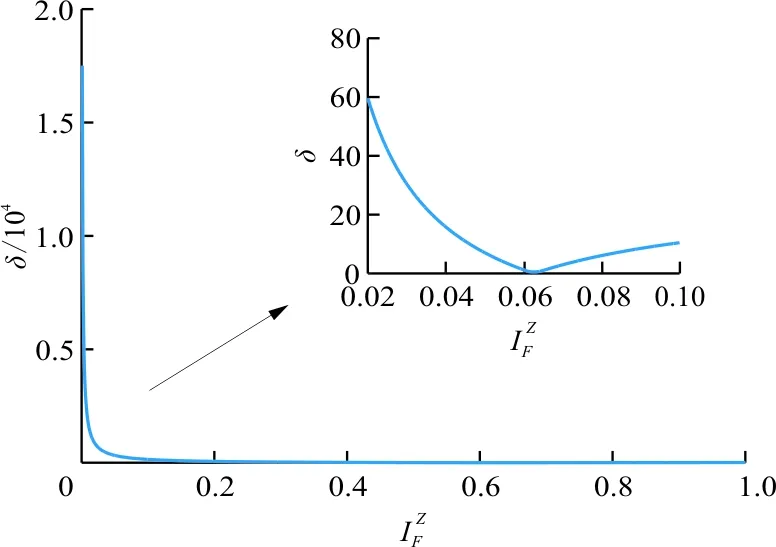
图11 δ关于变化规律

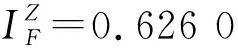
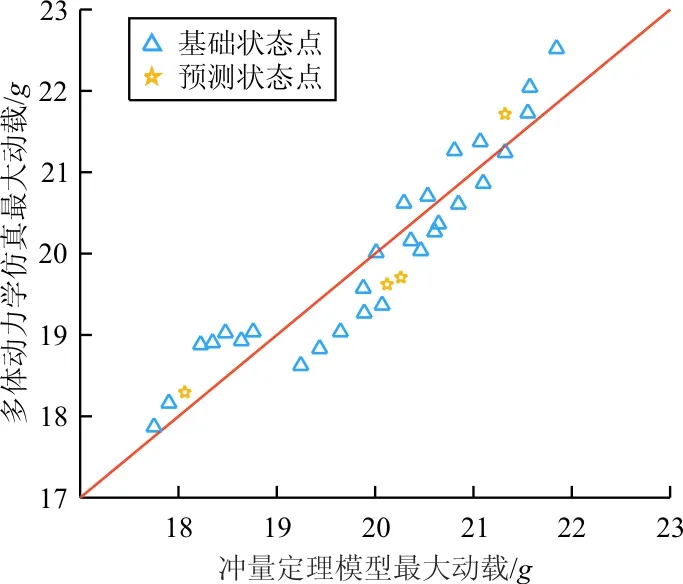
图12 多体动力学仿真与冲量定理模型计算结果对比

从图12可以看出：在基础状态点上，确定参数后的最大动载模型计算结果与多体动力学结果吻合度较好；同时，在预测点上，模型结果与仿真结果也有较好的吻合度，说明本模型是有效的。基于本节分析，给出本算例下，假人动载的冲量定理模型计算式为

(17)

4 结 论

(1) 基于定量系统仿真或者空投试验确定速度损失因子和动载变化因子后，本文模型可以快速确定最大动载，具有较好的工程应用价值。

(2) 在零零姿态下，假人动载关于空投速度和假人质量均正相关，与试验和仿真结果一致。

(3) 需要指出的是，目前模型选用了拉直速度作为计算参数，并不直观，所采用的匀减速模型也存在一定误差，后续可对出舱过程进一步研究，以空投速度为模型参数，应用更方便。