基于分时段与概率分布的滑行冲突预测研究
侯盼盼,王梓旭
(1.中国商飞上海飞机设计研究院 市场中心, 上海 201210)(2.中国民航大学 空中交通管理学院, 天津 300300)(3.北京大兴国际机场 运行管理部, 北京 102600)
0 引 言
随着我国经济的快速发展,民航的客运量和货运量都出现大幅的提高,机场变得越来越繁忙,因此对航空运行管理提出了更高的要求。目前航空运行管理面对诸多的压力,并且空中交通管理的瓶颈开始转移到机场方面。2009年召开的全国民航空管会议提出,民航空管系统要通过提高指挥能力,努力使每架航班空中飞行或地面滑行时间节约3 min。提高滑行效率必须以保证滑行航空器的滑行安全为前提,因此建立完整高效的滑行冲突预测体系显得尤为重要。
国外对于机场的滑行冲突已经做了较为深入的研究,J.Krozel等[1]初步探讨了机场场面冲突预测与解脱的方法;J.K.Kuchar等[2]提出了场面冲突检测审查和对场面冲突进行分类建模的方法;YANG L C等[3]提出了一种新的复杂报警事件设计思路与方法,使系统能够在线交替监测,并根据计算的物理测量报警值进行决策;D.Anuja[4]提出了一种模型,该模型基于神经网络进行航空器位置预测,从而减少运行冲突。
国内,Yu C[5]对关键区域滑行冲突进行了分析,建立了基于网络的仿真模型,并依据仿真结果提出了解决航空器推出冲突和减少航班延误的方法;徐肖豪等[6]引入了约束函数的概念,用以处理滑行道头对头冲突问题,对进一步的滑行研究具有重要的启发意义;尹嘉男等[7]在解决登机门分配问题时,把减少滑行冲突率作为一个目标来考虑;陈世林等[8]在解决滑行费用问题上以避免滑行冲突作为条件;王艳军等[9]在时间依赖最短路径算法的基础上,提出了一种回避冲突的动态滑行路径分配算法,用以解决机场场面航空器滑行路径分配问题;刘长有等[10]在研究航空器机场地面滑行时刻优化时把所有航空器的滑行速度均相同作为假设条件,忽略了不同航空器之间的速度差别;牟德一等[11]将滑行路径简化为图,在冲突预测时以两架航空器之间的时间间隔为冲突预测标准;丁建立等[12]基于飞机滑行时的冲突约束和跑道资源的动态分配, 采用改进蚁群协同算法与滑动窗口控制相结合的方法, 对滑行道进行优化调度。
上述文献中的滑行冲突预测鲜有对滑行过程的考虑,而滑行是航空器的一个运动过程。航空器在机场场面运行所经历的空间环节包括跑道系统、滑行道系统、停机位系统和廊桥系统等。为了更全面描述过程中的冲突预测,本文利用概率论基本原理,考虑航空器滑行过程,以航空器间距离与冲突概率双重标准分时段对滑行冲突进行预测。本文介绍的场面滑行冲突不考虑车辆等其他物体,只考虑作为运动实体的航空器在场面的运行冲突。
1 相关符号说明
本文使用的相关符号说明如表1所示,由于模型参数较多,表中列出主要参数,模型中零星出现的参数在后面单独说明。
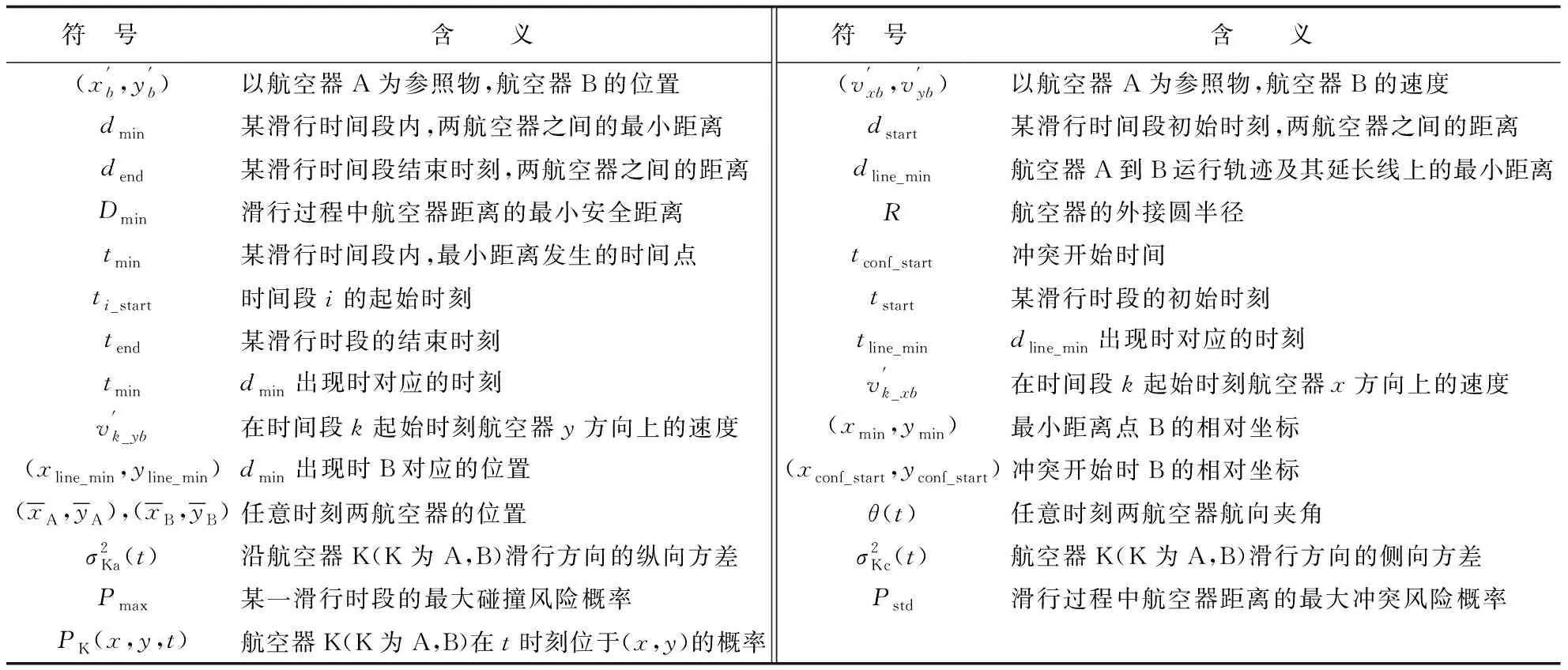
表1 符号说明
2 理想状态下的分时段冲突预测
在理想状态下,不考虑不确定运行误差以及突发情况,本文采用分段函数来描述航空器滑行时间与位置。
根据两航空器所经过的滑行路径交叉点情况,按照航空器到达交叉点时间的先后对两航空器的滑行路径重新划分为数目相同的多个滑行时间段,使得在每一个滑行时间段内航空器都保持方向和速度不变。两架航空器的滑行路径分别为T1,T3,T4,T5和T2,T4,T5,如图1所示。假设航空器A到达各点的时间为ta1,ta2,ta3,ta4,航空器B到达各点的时间为tb1,tb2,tb3,划分滑行时间段后,整体时间段则被分成六段,由ta1,ta2,ta3,ta4和tb1,tb2,tb37个时刻按照大小排序分割形成。
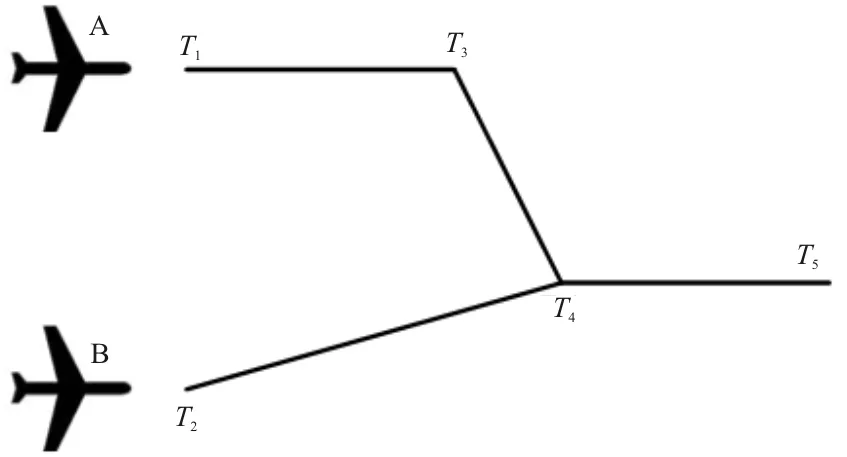
图1 航空器滑行路径

(1)
(2)
那么,对于任意时刻t,航空器B与A之间的相对位置可表示为
(3)
式中:tk为第k时段。
则,航空器A与航空器B所滑行路径的最小距离dline_min,对应时刻tline_min可表示为
(4)
(5)
航空器A与B最小距离dmin可以表示为
(6)
航空器A、B间距离最小的时刻tmin为
(7)
如果dmin>Dmin能够满足空间间隔标准,继续下一滑行时间段冲突预测;否则计算出最小距离发生的时间点tmin,冲突开始时间tconf_start,以及两航空器出现最小距离时,航空器B相对航空器A的坐标(xmin,ymin)。
在航空器B距离A的最近点(xline_min,yline_min),B的运动方向与B相对A位置向量垂直,如图2所示。

图2 某滑行时段A、B航空器位置示意图
因此有下述关系式成立:
(8)
求解可得:
(9)
(10)
那么,冲突开始时间tline_begin为
(11)
因此:
tconf_start=max (tstart,tline_begin)
(12)
那么,两航空器出现最小距离时,航空器B相对航空器A的坐标(xmin,ymin)可以表示为
(13)
(14)
求解完成后即可根据dmin,tmin,tconf_start和(xmin,ymin)进行冲突预测,结合预测结果辅助生成冲突报告。
3 考虑不确定因素下基于概率分布的冲突预测
第2节对理想状态下的航空器滑行冲突进行了预测,但是航空器在机场运行过程中很难按照理想状态运行。受航空器仪表指示误差、飞行员操作水平等各种不确定因素的影响,实际运行过程中航空器之间的冲突概率与理想状态下的预测结果存在一定的差异,为了更加贴近机场实际运行情况,在考虑随机误差的情况下,基于二维正态分布对滑行冲突进行预测。

航空器滑行误差可以看作是由许多微小而独立的随机变量组成,R.Paielli和H.Erzberger经过实际飞行数据研究得出,航空器在空中飞行时位置预测误差沿着航向、侧向和垂直方向是相互独立的[14]。纵向方差与t2成正比[15],侧向方差随飞行时间的增大而趋于某一个饱和值。其整体误差满足均值为零的正态随机分布,因此在场面运行时,借鉴上述结论,可将航空器的位置分布分为两个正交的水平分量:
(15)
式中:ra为纵向、侧向方差的增长率,与设备精度、飞行员操作水平等有关。
(16)
式中:rc为侧向方差的增长率,与设备精度、飞行员操作水平等有关。
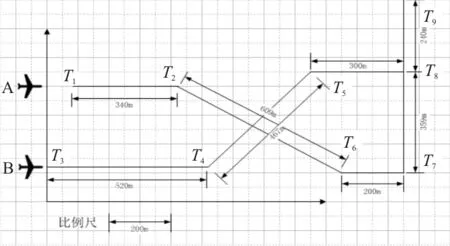
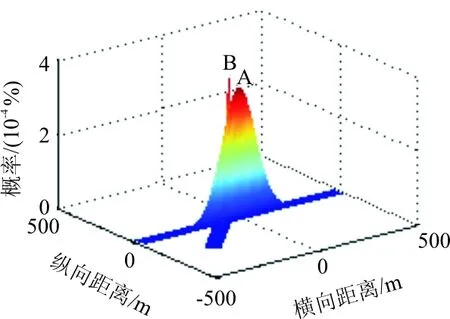
对某一滑行时段进行研究,将该时段以一定步长逐点计算冲突概率,求出最大冲突概率Pmax。当Pmax 设航空器A在t时刻位于(x,y)的概率为PA(x,y,t),航空器B在t时刻位于(x,y)的概率为PB(x,y,t)。 那么,PA(x,y,t)为 (17) 在计算航空器B出现在(x,y)点的概率时,需要进行坐标系转换,转换后坐标原点为B′,在t时刻航空器A与B所在坐标系x轴的夹角为θ(t),由航空器之间最小距离计算的过程可以得出点(x,y)转换坐标系后的坐标(xB,yB)为 (18) 此时,PB(x,y,t)可以表示为 (19) 则两者的滑行冲突风险可表示为 (20) 其中S需满足以下条件: 航空器碰撞风险图如图3所示,A,B为航空器的平均位置,A′,B′为航空器可能出现的实际网格位置。以航空器的几何中心为中心,一定长度R作为航空器的外接半径,绘制保护区,如果两个保护区有重叠部分,则视为有碰撞冲突,冲突概率为两航空器出现在各自网格位置概率的乘积。将所有两两网格的冲突概率叠加后,即为两航空器的冲突概率。整体预测流程如图4所示。 图3 航空器碰撞风险图 图4 冲突预测流程示意图 航空器A,B分别沿着T1、T2、T6、T7、T8、T9以及T3、T4、T5、T8、T9路径滑行如图5所示。各段滑行路径长度已经标出。两航空器速度VA=8 m/s,VB=7 m/s。tAT1=0 s时刻A从T1由静止出发,tBT2=45 s时刻B从T2由静止出发。航空器A、B按照图5所示的情况运行,根据本文所建立数学模型,应用Matlab编程仿真计算,得到航空器运行风险分析图,如图6所示。 图5 算例滑行路径示意图 (a) 滑行路径 (b) 冲突概率随时间变化 (c) 冲突概率随时间变化(指数表示) (d) 航空器之间的距离 从图6可以看出: (1) 如果以Dmin=100 m为冲突预测标准,由dmin可判断出,两航空器在滑行时间段2、3、4存在距离小于100 m的时刻,需要加以规避冲突,在其他时间段则满足冲突预测标准。 两航空器在121 s的时候距离达到最小值8.6 m,即为图6(d)星号所标示位置。 (2) 如果以Pstd=1.5×10-5为标准,如图6(c)所示,在92 s之后,航空器之间的风险冲突几乎一直大于Pstd。因此在滑行时间段2~7,都需要加以规避冲突。 (3) 综合上述两项结论,航空器在92 s之后一直存在风险冲突,需要规避冲突。 (a) t=90 s (b) t=120 s (c) t=150 s (d) t=180 s (a) t=90 s (b) t=120 s (c) t=150 s (d) t=180 s (1) 相对于将连续时间离散化的方法,采用基于分段函数的计算方法能够有效降低计算量,较好地解决了航空器路由规划的优化性和实时性之间的矛盾。 (2) 在滑行中存在不确定因素的情况下,需要考虑航空器侧向和纵向方差对滑行冲突的影响以及航空器位置误差随时间的累积效应。 (3) 在滑行冲突预测过程中应同时以最小安全距离和最大冲突风险概率为标准,确保航空器的滑行安全。实际运行中可与机场监视数据结合使用,作为冲突探测的理论模型,或通过仿真软件等技术手段进行可视化监控。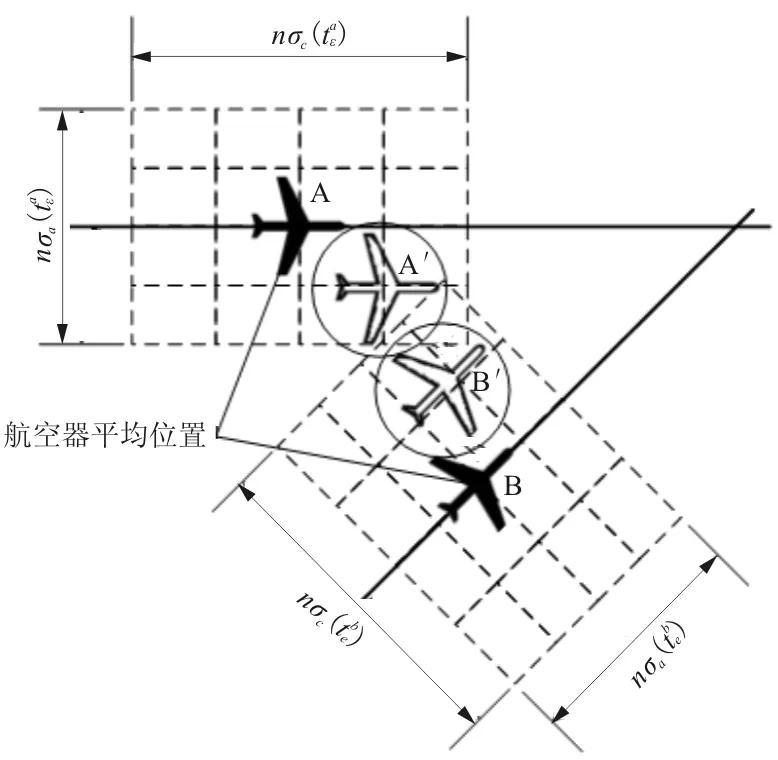

4 算例分析








5 结 论

