民用飞机客舱应急撤离仿真算法研究
王霁飞,刘龙权
(上海交通大学 航空航天学院, 上海 200240)
0 引 言
飞行安全是飞机研究中最重视的部分,运输类民航客机适航标准CCAR第25部803条款要求:对于客座量大于44座的飞行器,必须表明在应急情况下其最大乘坐量的乘员能在90 s内从飞机撤离至地面[1]。因此,民航客机在通过适航认证并正式运营之前,必须表明其客舱安全性满足适航规章的要求。然而,一次真机试验需要涉及许多人员、设备和仪器,费用较高,且具有较高的危险性。以波音公司为例,一次客舱逃生试验,总计耗费金额达到100万美元以上[2]。1972-1980年间,FAA的7次全机逃生试验共涉及人员2 571人,造成其中166人受伤。1981-1991年间,FAA全机逃生试验共涉及3 761人,受伤人数达到212人[3]。1991年,在对MD-11宽体机进行应急撤离疏散实验时,一位女性测试者因受伤而永久性的瘫痪[4]。2006年A380完成逃生测试时一人脚部骨折,多人受伤[5]。与之相比,数值仿真模拟既安全且可重复性高,又可以模拟各种极限情况,因此飞机客舱逃生数值模拟可作为试验的有益补充。
目前国外已长期开展飞机客舱安全逃生相关仿真研究。据文献调研,FAA早在1962年就已开展乘客应急撤离模型相关研究[6];1970年,FAA开发了GPSS软件,这是第一个能用来模拟飞机客舱应急撤离仿真的软件;此后国外陆续开发GA、AIREVAC、MACEY、airEXODUS等多个用于民航客机90 s应急撤离的仿真算法和软件[7],其中英国格林威治大学开发出商用软件airEXODUS能较好地模拟仿真各种应急撤离的场景,但关于飞机部分其软件对外保密[8-10]。
相比之下,国内对于飞机客舱逃生仿真的研究相对较少。李杰等[11]研究了飞机应急撤离的元胞自动机模型,并在DELMIA平台实现建模和三维演示;徐进津[12]研究了飞机客舱疏散仿真的人为因素,总结了客舱和乘客的属性以及一些人为因素数据。上述文献中均采用元胞自动机模型模拟疏散人群的属性,把疏散人群视为相同粒子,忽视了个体的差异化,与真实撤离实验存在一定差别。陈晨、杜红兵等[13-15]运用元胞自动机模型,并借鉴了智能体模型,开发仿真软件CabinEvac,并研究乘客的应急心理状态,但其对心理状态的考虑并不全面,且未与相同状态下的逃生试验结果进行对比验证。
智能体模型把关注点放在疏散体身上,认为模型对象能在一定的环境下,具有一定的行为规则和学习能力,通过感知外界因素调整自身的状态,最终完成目标[16]。这种模型的优点在于其能体现个体的差异性,使模拟仿真更接近于真实。
本文采用智能体模型,建立逃生智能体的行为准则,以最优路径算法A*算法为主要行为依据,根据拥挤情况选择在A*算法中适合飞机的估值函数;结合个体与个体之间的协助与阻碍影响,个体与环境的影响,建立客舱应急撤离的仿真模型;将算法结果与前人实验结果和权威软件airEXODUS仿真结果进行对比。
1 疏散人群的智能体模型设计
1.1 智能体模型
智能体模型来源于人工智能,指的是模型对象在一定的环境下,具有一定的行为规则和学习能力,最终完成目标任务[16],这是一种自下而上构建的社会模型[17]。
基于智能体模型理论,结合运输类飞机适航标准,本文中的智能体模型遵循的行为规则分为三大子规则,分别为路径抉择规则、移动规则和交互规则,如图1所示。在路径抉择时,智能体通过A*算法求取各逃生出口对应的最优路径,然后比较不同出口的最优路径,最终做出选择;在移动规则下,疏散体的移动速度受到初始移动速度与其他系数的影响;在交互规则下,拥挤、恐慌和互助分别对路径抉择中的A*算法估值函数和影响速度的系数产生影响。

图1 智能体模型的移动规则
1.2 路径抉择规则
在路径抉择上,每个疏散智能体均选择最优路径的方法前进,本文采用在最优路径研究领域被广泛采用的A*算法。
1.2.1 A*算法原理
A*算法是一种人工智能中典型的路径启发式搜索优化算法,通过选用合适的估值函数F(n),朝着最可能的值进行求取,最终得到从起点S到终点E的最短且最合适的路线,其原理图如图2所示。

图2 A*算法原理图
A*算法的步骤:
(1) 设置开放(open)和关闭(close)两个列表,起点定为S,终点定为E。
(2) 从S开始,把S放入open列表中。
(3) 判断open列表是否为空,若为空,则宣告路径寻找失败,退出循环。
(4) open列表为非空集合,选取open列表中F(n)最小的节点T,将节点T从open列表中删除,放入close列表。
(5) 检查节点T是否为终点E,若是终点E,则找到路径并退出循环。
(6) 若节点T不是终点E,则把节点T周围的可扩展节点Ti(上下左右且不出界和非墙节点)做预处理,计算Ti节点的F(Ti),并判断Ti。若Ti不在open和close列表中,则加入open列表,并定义其父节点为T。若Ti已经在open列表中,则比较当前F(Ti)与原先的F′(Ti):F(Ti)较小,则说明当前路径更优,并更改父节点为当前T,用F(Ti)代替F′(Ti);F′(Ti)较小则说明原路径更优,因此跳过。若Ti已经在close列表中,则跳过,处理下一个节点。
(7) 返回步骤(3),直到在步骤(3)或步骤(5)时跳出循环。
1.2.2 A*算法的估值函数
估值函数F(n)是A*算法中的一个核心,选择合适的估值函数能正确地得到目标至终点的最优路径,A*算法选择F(n)=G(n)+H(n)作为估值函数,其中G(n)为从起点S到达一个节点n所已经付出的代价,H(n)为从节点n到终点E所估计需要付出的代价。
在路径搜索中曼哈顿距离常被用于估值函数。曼哈顿距离指的是两点之间的x轴距离和y轴距离之和[18],即若存在两点S(x1,y1)和E(x2,y2),则曼哈顿距离L为
L(S,E)=|x1-x2|+|y1-y2|
(1)
飞机的情况较为复杂,人与人的交互也对估值判断有较大的影响,因此估值H(n)=L(S,E)+Hinter(n),其中Hinter(n)为人群交互所产生的估值函数影响变化。
1.3 交互规则
人与人之间的交互主要对模型体有两方面的影响,拥挤和恐慌会对路径抉择产生影响,同时恐慌与互相帮助也对人的移动速度产生了影响。
1.3.1 拥挤系数
拥挤对路径抉择具有较大的影响,拥挤的人数会被折算成对应的等价距离。
定义拥挤距离Hinter(S,E)=μ×people(S,E),其中people(S,E)指的是从起点到终点两个顶点所组成的矩形中所包含的人数,μ为拥挤系数。
因此,A*算法中估值函数H(n)=L(S,E)+Hinter(S,E)
1.3.2 恐慌系数
恐慌主要产生两方面的影响,一方面适当的恐慌会使人紧张,促使疏散体移动速度变快[19];另一方面过度的紧张会使得疏散人群变得不理智,产生移动停滞或反向移动等现象[20]。
本文采用SIS模型和情绪衰减管理模型[21]模拟疏散人群的恐慌现象。
恐慌情绪会对路径决策产生影响,人群分为两类人:易感者(Susceptibles)与感染者(Infectives)。易感者为情绪接收者,不向外传递情绪;感染者为情绪传递者,同时也能接收情绪。易感者与感染者可互相转变,其转变零界点为情绪阈值η。当情绪值达到ηc时,其行为呈现非理智状态,将出现停滞或随机移动的行为现象。
初始时刻的恐慌系数k通过正态分布确定[21],如式(2)所示。
kt=0~N(μk,σk)
(2)
式中:k为恐慌系数;μk为正态分布的均值;σk为正态分布的标准差。
由于恐慌程度与年龄性别有关,建立不同年龄段和性别的初始恐慌因子,如表1所示。

表1 不同年龄、性别人群的初始恐慌因子
某一时刻某一人物恐慌系数k的计算公式,如式(3)所示。
(3)

一般情绪传递半径为一格到两格[21],本文选用两格作为情绪传递半径。
(4)
疏散人群的恐慌会随时间衰减,并且会离出口相接近时大幅度衰减。因此情绪衰减速率kpdecay的计算公式,如式(5)所示。
(5)
式中:α为疏散体在靠近出口处的情绪衰减速率,取值0.8;β为疏散体正常情况下的情绪衰减速率,取值0.1;tp为疏散体收到情绪传递的时间;d为疏散体离最近出口的曼哈顿距离;Rdoor为出口相近处的临界曼哈顿距离。
当恐慌系数kp<ηc时,疏散体呈现较为理智状态,此时kmove=λkp,其中λ为激励调节因子;当恐慌系数kp≥ηc,疏散体呈现不理智状态,呈现停滞。
1.3.3 乘客之间的互相协助因子
互相帮助可以使得疏散者的移动速度变快。根据AASK的飞机事故数据库调查显示,49.5%的乘客会在飞行过程中与同伴一起同行,其中65%为家庭关系,16%为朋友关系,8%为同事关系,11%为其他关系,不同的关系决定了帮助的程度[22-23]。在同伴关系中,9%的乘客在真实飞行过程中,提供了他人帮助,其中男性占据68%,女性占据36%。
因此协助系数s:
(6)

1.4 移动规则
1.4.1 乘客的速度
人员最大的移动速度取决于年龄、性别,是否携带婴儿等其他因素影响,因此采用公式Vk=random(Vkmax,Vkmin)×λ,其中Vkmax为人员移动速度最大值,Vkmin为人员移动速度最小值,λ为速度影响系数。
人员最大移动速度采用GALEA整理的民机人员应急撤离速度分布统计数据,结合Fruin实验统计[20],数据是对于目前应急撤离实验录像影音中人群的速度统计得到,如表2所示。

表2 不同年龄性别人群应急撤离速度统计[24]
小于2岁的婴儿被视为无行为能力者,且依附于其他人员且弱化该人员逃生速度,本文采用减少被依附人员30%的移动速度。
1.4.2 速度影响系数
速度影响系数λ主要受到恐慌系数k、互助系数s和障碍物的影响。
在客舱中障碍物分为两种,可翻越式与不可翻越式。其中可翻越式主要为乘客的行李、座位处的把手,不可翻越式主要为座位、机上厨房与洗手间。根据《运输类飞机适航标准》附录J[1],在适航逃生时,会有乘客人数一半的行李、毯子、枕头等其他类似物品放在过道或出口造成轻微障碍。不同障碍物的速度影响系数如表3所示,得到速度影响系数λ=kmove×s×λelse。

表3 不同障碍物的速度影响系数
2 飞机客舱模型
2.1 机型选择B737-700机型
本文选用B737-700120座级机型进行数值仿真。该机型客舱分布图如图3所示,左右两侧呈现对称状态,每侧各有三个应急出口,共120个座位,为B737-700全普舱型机型。

图3 B737-700客舱模型图
2.2 应急设备使用情况
2.2.1 安全门使用情况
按照《运输类飞机适航标准》25.807条[1],许可的最大乘客数取决于机身上每一侧的应急出口类型和数量,可容纳最大乘客数规定如表4所示。

表4 应急出口类型与最大乘客数对应表
C型出口需在10 s内完全展开,其他型出口需要在6 s内完全展开[1]。结合文献[25]可得C型、Ⅰ型与Ⅱ型门大致开门时间如表5所示。

表5 各类型门开门时间
在适航审定过程中,局方要求使用的安全门是开启一半的门,根据中轴线对称的每两扇门使用其中一扇作为可用出口,用来测试能否通过90 s的应急撤离试验。由于在仿真计算过程中,左门开启与右门开启影响甚微,因此全部使用一侧作为开口。
2.2.2 逃生滑梯的使用情况
查阅文献[26],得到在正常离地高度3.5 m,滑梯展开与地面呈35°时,乘客与滑梯之间的摩擦系数为0.4,单人下滑时间为1.91 s。B737-700舱门离地高度约为2.7 m。因此t单人≈1.91/3.5×2.7,为1.47 s。按照CTSO-C69c标准,一段滑梯上应能同时承载3人[27],因此当t=1.47/3=0.49 s时,下一位疏散体即可使用滑梯。
2.3 应急撤离时间
应急撤离时长由以下两部分组成:
(1)T1——乘务员抵达相应安全门,若对应大门可用,则打开门,滑梯充气的时间。
(2)T2——乘客开始准备撤离,在开门过程中排队,开完门后依次乘坐应急逃生滑梯离开客舱的时间。
总撤离时长T=T1+T2。
3 模型有效性验证
为了验证数值仿真模拟的有效性,本文采用模拟B737-700机型,将本文数值模拟结果与airEXODUS软件仿真结果[24]和前人实验结果[28]进行对比。模拟客舱内含有60名志愿者,包含38名青年男性和22名青年女性。客舱段选用了前十排座椅(总计60个座位)和两个前排I型门。在真实实验中一共重复四次,airEXODUS软件仿真模拟12次,本文采用相同情况进行模拟20次结果,取最大与最小的模拟时间与实验结果进行对比图如图4~图5所示。
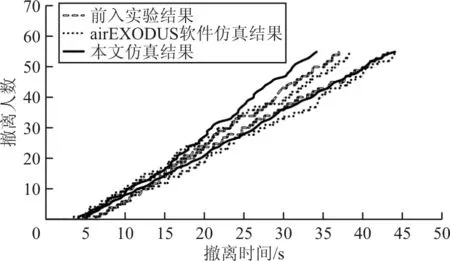
图4 应急撤离数值模拟结果、前人实验结果与airEXODUS软件模拟结果对比图

图5 应急撤离数值模拟20次结果频数分布图
从图4~图5可以看出:本文的数值模拟结果与真实实验结果和软件airEXODUS仿真结果吻合(airEXOUDS仿真软件为航空器撤离权威学者E.R.Galea带领团队开发[8-9,22-24]),在15~30 s,本文仿真结果较真实撤离有更宽的覆盖范围,这是因为真实实验一共由四次组成,因此并没有全面覆盖应急撤离的真实时间范围;同时,平均撤离时间较为接近,在25~40 s部分实线(本文模拟结果)包在长条点状线(前人实验结果)以外,较为合理。因此本文的仿真结果有效。
55名乘客疏散时间的数值模拟结果与前人实验结果和airEXODUS仿真结果对比如表6所示,可以看出:本文算法模拟的乘客疏散时间与前人实验结果和airEXODUS仿真结果接近。

表6 55名乘客疏散时间的数值模拟结果和
4 结 论
(1) 将适用于飞机疏散的A*算法仿真结果与前人实验结果和国外权威软件仿真结果进行对比,对比结果表明本文仿真算法是有效的。
(2) 本算法与传统应急疏散撤离中使用的元胞自动机模型相比,考虑了疏散体之间的差异性,是一种从疏散体本身出发的算法。利用本算法,可以使仿真模拟更接近真实疏散情况。但本算法的求解效率还有待进一步研究与改善。

