基于自适应动态规划的反高超武器微分对策制导律

孙磊，付斌，万士正，常晓飞，闫杰

(西北工业大学 航天学院， 西安 710072)

0 引 言

随着各国高超声速飞行器技术的发展，各型演示验证项目的武器化进程不断加快，以我国的“DF-17”、俄罗斯的“先锋”为代表的高超声速武器已经陆续进入到现役武器装备行列。相比于传统武器，高超声速武器具有飞行速度极快、自主博弈机动能力强、飞行弹道多变等突出特性，在对其进行拦截时，传统拦截制导方法拦截能力弱，使得我军在反高超声速武器拦截作战中，以“一对一”进行拦截时任务失败风险较大，以“多对一”进行拦截时，综合作战效能较低。

为了解决高超声速武器的拦截问题，研究人员提出了许多新型制导方法。李炯等[1-2]针对反高超声速武器拦截制导问题设计了一种非奇异快速终端二阶滑模制导律，并且针对侧窗探测的动能拦截反高超声速武器设计了一种制导律，其在对目标进行拦截时需要始终保证导引头侧窗对于目标的指向，从而实现对目标的探测；叶继坤等[3]基于经典的微分几何理论，对末制导中的弹目运动模型进行了空间几何分析，并设计了二阶滑模微分几何制导律，克服了不确定性的影响，保证了系统的鲁棒性和制导精度；雷虎民等[4]针对反高超声速武器拦截问题，设计了一种基于零控脱靶量在有限时间收敛的制导方法，通过自适应滑模理论与有限时间稳定控制理论的结合，选择解耦的纵向面与水平面上的零控脱靶量作为滑模面，给出了制导律形式，并且证明了制导律的有限时间收敛特性。

上述方法均将目标的突防策略考虑为一种固定的机动模式，当未来战场中，目标的机动将会更加智能，可能会针对我方机动而选择更加有针对性的突防策略。因此研究人员开始研究一种基于博弈微分对策的博弈制导方法。花文华等[5-6]基于变速导弹模型的非线性情况进行了制导律设计，并通过选取合适状态量对模型进行了线性化，推导出了微分对策制导律形式，还针对带有攻击角约束的情形进行了微分对策问题的指标设计，并通过系统的降阶，实现了解析形式的制导律求解；李迁运等[7]针对大气层内直/气复合飞行器进行了微分对策制导问题中，直/气复合控制系统对策空间分布的研究，并对策略空间进行了优化；Y.Oshman等[8]基于微分对策理论设计了一种针对未来高机动无人作战飞行器的制导方法，其主要创新点是采用了通过对目标姿态信息的解译，实现了对目标飞行状态的估计；A.Green等[9]在水平面内设计了一种追逃制导律，追逐方带有末端速度要求，逃逸方速度恒定但是带有机动能力，并根据追逃双方的初末条件给出了最优制导策略；V.Turetsky等[10]针对未来可能出现的强机动能力弹道导弹拦截问题，分析了两种基于追逃对策的制导律，对比结果显示，在相同的初始条件与参数下，仅考虑零控脱靶量作为性能指标的制导律所形成的攻击区较考虑能量最优的制导律有更大的攻击区。另外还有许多研究者采用了微分对策问题的建模方法进行制导律设计，但是在求解过程中多数都是采用了简化的非线性模型或者是近似模型，其求解精度在一定程度上会受到影响。

为了更好地求解微分对策条件下的纳什均衡解，研究者引入自适应动态规划(Adaptive Dynamic Programming,简称ADP)算法对这类最优化问题进行求解[11-17]，其中Sun J等[18-19]在拦截制导中采用自适应动态规划算法，但是其所选用的回报目标是终端零控脱靶量最小，而本文所采用的方法是每一时刻的视线角速度最小，相较之制导过程更平稳。

ADP算法具有求解速度快、计算精度高等优点，能够很好地应用于制导律设计过程。本文针对高超声速目标机动打击特点，采用自适应动态规划的方法进行拦截弹制导律求解。首先，针对高超声速目标拦截问题中的连续非线性问题进行微分对策问题建模；然后，利用近似动态规划算法对连续非线性系统微分对策问题进行求解；最后，基于高超攻防对抗对所给出的方法进行仿真验证。

1 微分对策制导问题建模

为了准确地描述微分对策问题，从而进行解的求取，需要对拦截弹与目标进行拦截相对运动的微分对策问题建模。

1.1 弹目相对运动关系建模

为了方便地描述末制导阶段的弹目相对运动，从而给出制导律推导时所需要的部分运动方程，本节对弹目相对运动关系进行简单的描述和定义。为了简化推导，一般可以将纵向与横侧向平面直接解耦后分开考虑。在纵向平面内，末制导阶段纵向平面内弹目运动关系如图1所示。

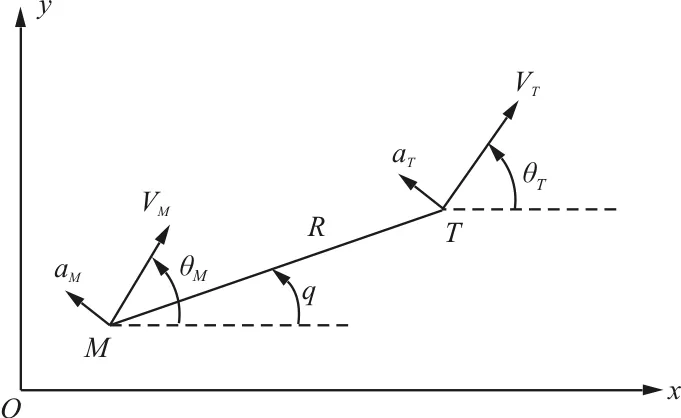
图1 末制导阶段纵向平面内弹目运动关系

图1中，Ox轴与Oy轴构成了弹目遭遇平面，拦截弹以质点M表示，其速度为VM，速度倾角为θM；在垂直于速度的方向上，拦截弹具有加速度aM；高超声速飞行器目标以质点T为表示，其速度为VT，速度倾角为θT；在垂直于速度的方向上，高超声速飞行器具有加速度aT；弹目相对距离为R，弹目视线角为q。

弹目间相对位置按照极坐标表达形式(R,q)的数学表达式为

(1)

(2)

在推导过程中，拦截弹与目标的运动模型也可以简化的表示为

(3)

拦截弹的速度VM与目标的速度VT在末制导阶段也可以认为是不再变化的。

对式(2)求导，可得：

(4)

将式(3)代入式(4)可得：

(5)

整理后可得：

(6)

选取系统状态为

(7)

系统状态方程可以写为

(8)

1.2 微分对策问题一般化描述

针对式(8)考虑连续非线性系统为

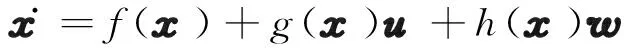
(9)

式中：x∈Rn为状态向量；u∈Rm为控制向量；w∈Rp为扰动向量；f(x)∈Rn、g(x)∈Rn×m、h(x)∈Rn×p均为光滑可微函数，分别为系统内动态方程、控制方程与扰动方程。

定义指标函数为

(10)

当追逃双方对于某一状态x(t)，采用控制策略u(x)与扰动策略w(x)时，可以用状态值函数(如式(11)所示)对追逃策略进行评价。

(11)

对式(11)求导后可得：

(12)

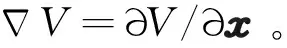
可以定义汉密尔顿函数为

H(x,u,w)=U(x,u,w)+

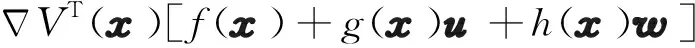
(13)

假设这个微分对策问题有唯一的鞍点解，且鞍点解满足纳什平衡条件，如式(14)所示。

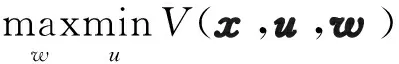
(14)

则根据Bellman方程最优性原理，有如下关系：

(15)

对于u*与w*必须满足最优性必要条件为

(16)

可以得到最优解形式如式(17)所示。

(17)

将式(16)、式(17)中的最优控制u*与w*代入汉密尔顿方程，得到：

xTQx+

(18)

2 连续非线性系统微分对策问题的近似动态规划解法

2.1 自适应动态规划算法流程

对值函数的表达式进行变形得到：

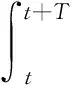
(19)

此时，纳什平衡条件可以重新整理为

(20)

根据自适应动态规划算法中常用的值迭代算法，有如下求解流程：

(1) 对于状态S初始化值函数，并计算t+T时刻的值函数；

(2) 根据t+T时刻值函数，以及t时刻的奖励函数U，计算当前时刻值函数的估计目标值；

(3) 根据目标值修正值函数的估计函数；

(4) 根据值函数修正值计算最优策略值。

值函数更新公式为

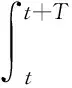
(21)

策略更新公式为

(22)

基于上述方法，设计一个Actor-Critic架构的算法框架，通过对基于神经网络的评价函数进行值迭代，不断地优化出一个最优的值函数，示意图如图2所示。

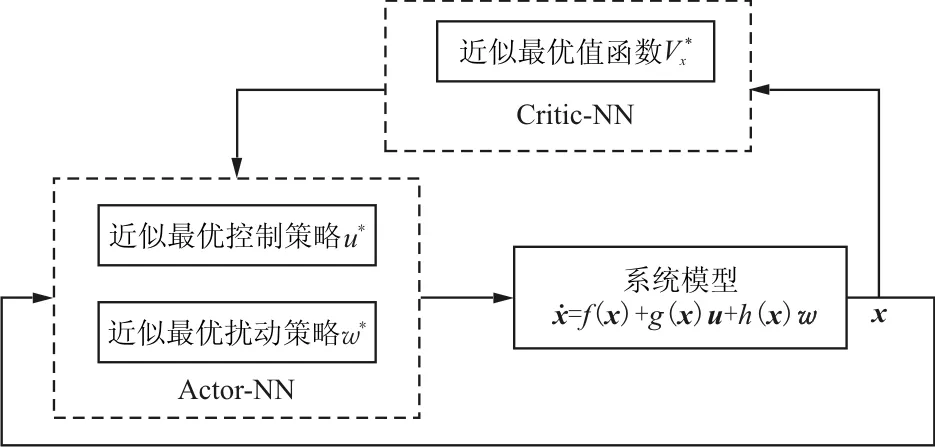
图2 自适应动态规划算法的Actor-Critic架构

2.2 自适应动态规划算法实现

本文给出值函数的神经网络近似形式的表达式为

(23)

式中：σ(x)为神经网络拟合基函数，以状态的4次项的齐次形式进行状态组合，需要设置对应的权值WVi。

值函数关于状态的偏导数则可表示为

(24)

按照值迭代公式，可以计算得到当前时刻的目标状态值函数更新值应为

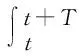
(25)

当前时刻的状态值函数神经网络近似值为

(26)

近似误差为

(27)

为了采用误差值对近似神经网络进行修正，本文采用梯度下降法，建立误差指标函数为

(28)

根据梯度下降法，给出值函数神经网络的权值修正算法为

(29)

式中：αV为学习率，表示对于梯度下降的比率更新。

其中，

(30)

3 末制导仿真

3.1 仿真参数设置

为了验证自适应动态规划算法的有效性，进行基于数字仿真的实验验证。仿真初始条件如表1所示。

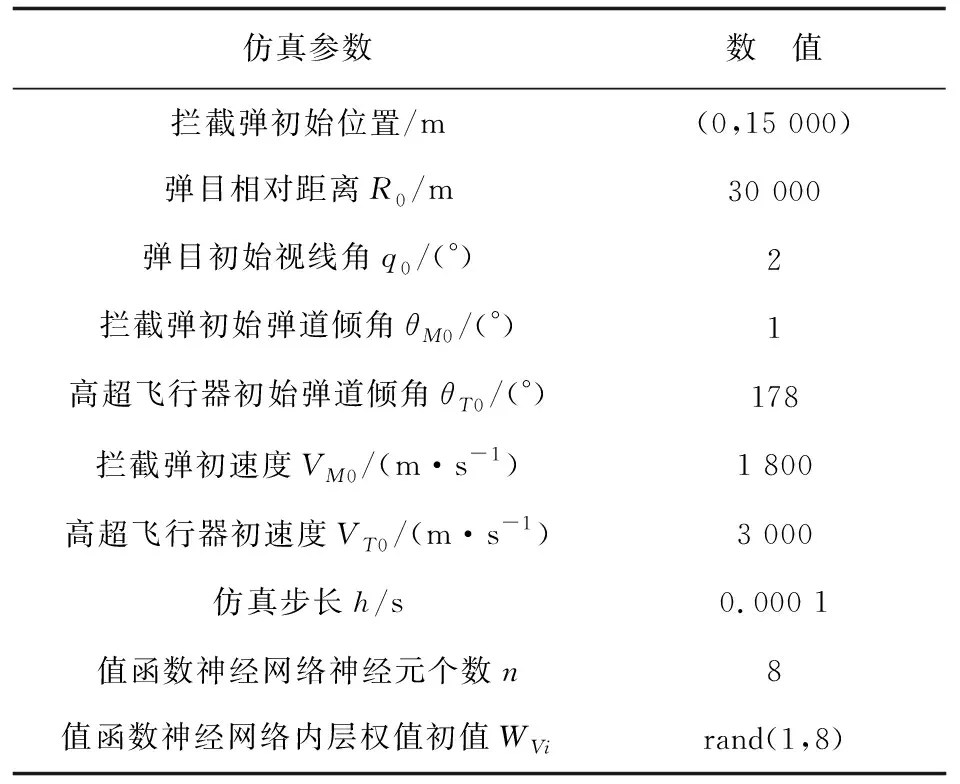
表1 仿真初始条件

3.2 对比制导律方法简介

周狄[20]提出的基于滑模变结构方法的最优滑模制导律(Optimal Sliding Mode Guidance，简称OSMG)在制导拦截问题中表现出了优异的特性，相比于增广比例导引算法，其不需要知道目标机动的具体大小，可根据当前状态与滑模面的关系自适应给出相应的补偿机动。OSMG制导下的拦截弹会按照给定的滑模面趋近于目标，OSMG算法具有较高的拦截精度，并且其需用过载相比于比例导引类算法而言会更小。其表达式为

(31)

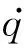
3.3 仿真结果与分析

考虑目标178°和175°两种弹道倾角情况下，对基于ADP的微分对策制导律和基于OSMG的制导律进行对比仿真，相应拦截轨迹和拦截过载结果如图3～图6所示。在目标弹道倾角为178°时，基于ADP的微分对策制导律与基于OSMG的制导律拦截效果均较为理想，不仅指令过载较小，且拦截精度较高。但是，当抬高目标初始弹道倾角到175°时，拦截效果出现了较大差异。

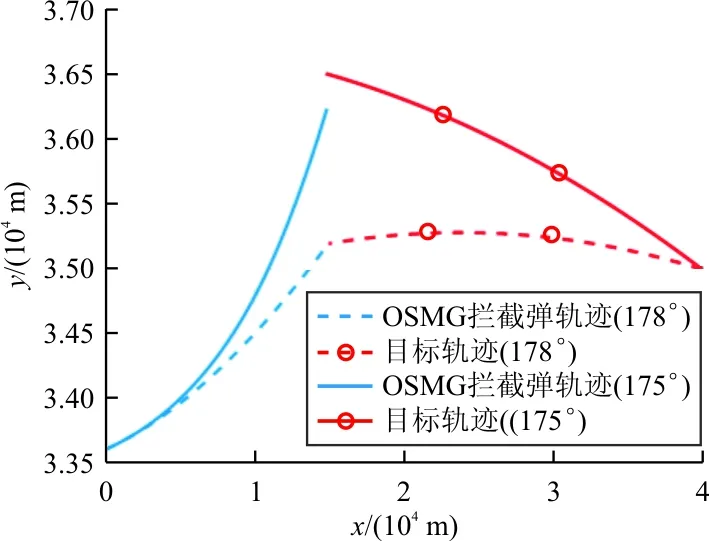
图3 OSMG制导律在两种情境下的拦截轨迹

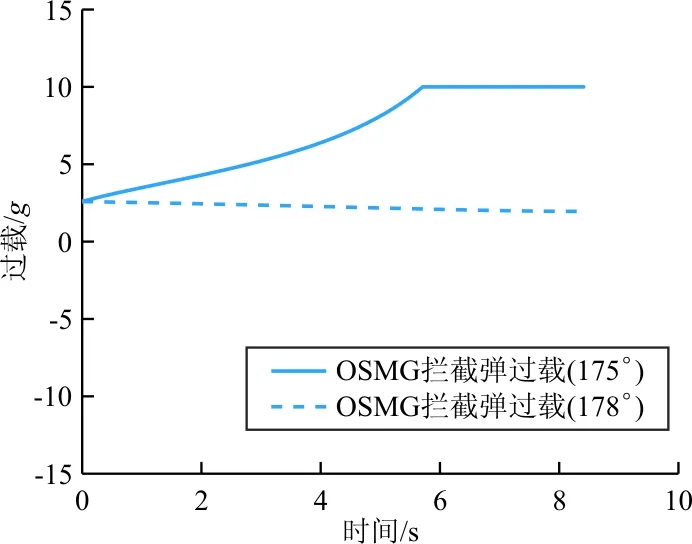
图4 OSMG制导律在两种情境下的拦截过载

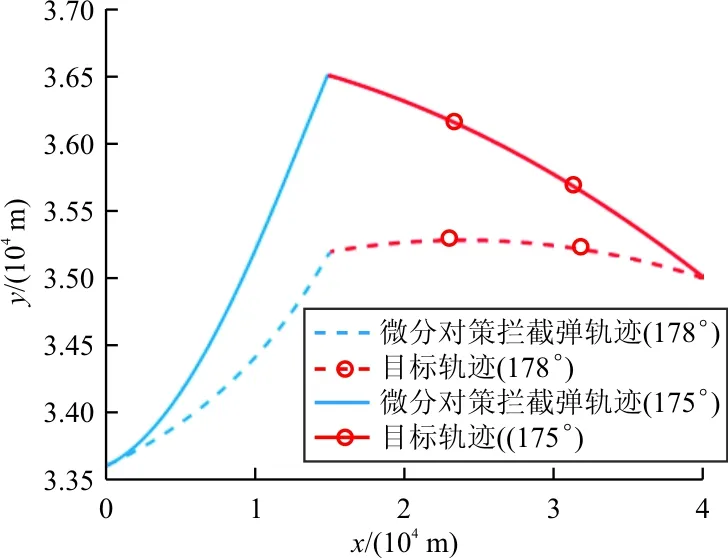
图5 ADP微分对策制导律在两种情况下的拦截轨迹

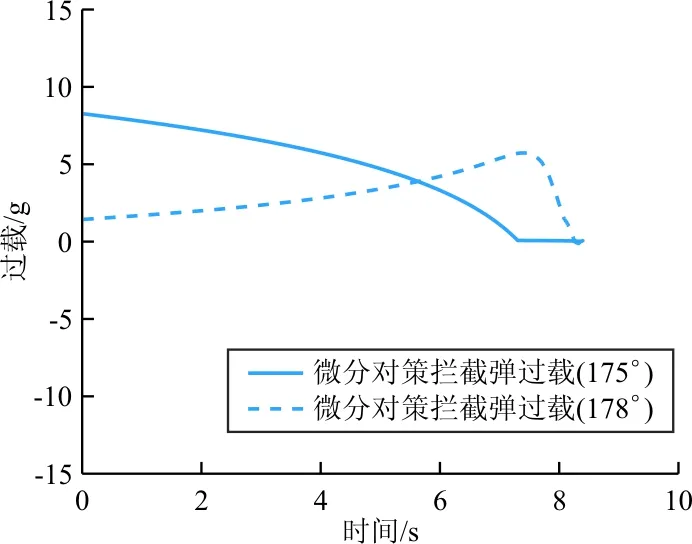
图6 ADP微分对策制导律在两种情况下的拦截过载

从图3可以看出：当目标初始弹道倾角较大时，迎头拦截趋势较好，拦截效果也较好；当目标初始弹道倾角减小时，弹目间迎头误差较大，拦截弹需要进行较大程度的修正。但是由于OSMG这种基于视线角速度的比例导引律类制导律，初始视线角速度较小的情况下，修正较慢(过载指令小)，当与目标逐渐接近时，逐渐提升过载，但由于时机较晚，过载即使饱和(过载已经达到了10g饱和，如图4所示)，也无法实现对目标的拦截。

基于ADP的微分对策制导律受到目标弹道倾角影响较小，适应性更好。从图 5可以看出：不论目标初始弹道倾角是175°或是178°，均对目标实现了较好的拦截。从图 6可以看出：当目标弹道倾角减小时，初始对准误差较大，基于ADP的微分对策制导律采用较大过载实现了指向调整；随后，拦截弹过载指令逐渐减小，直至拦截碰撞前收敛至0附近，这是因为基于ADP的微分对策制导律选择了预测零控脱靶量进行设计的，当预测零控脱靶量较小时，拦截弹不再进行机动来实现对目标的拦截。

综上所述，本文设计的基于自适应动态规划的微分对策制导律能够较好地实现对高超声速目标的拦截，并且对于初始迎头态势要求不高，适应性更好。

4 结 论

(1) 本文针对具有博弈突防能力的高超声速目标设计了一种基于自适应动态规划算法的微分对策制导律，这种制导方法能够快速便捷地对微分对策问题的纳什均衡解进行学习。

(2) 所提出的方法能够很好地实现对高超声速目标的拦截。相较于最优滑模制导律，该方法的适应性更强，拦截效果更好。