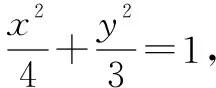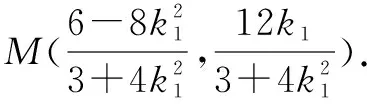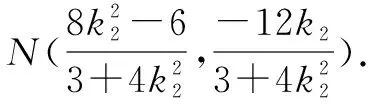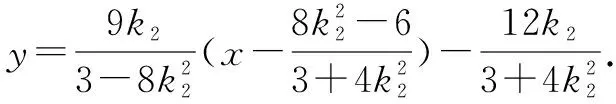例谈一题多解在解析几何中的应用

于庆丽

(江苏省宿迁市泗洪姜堰高级中学 223900)

新课程视野下高考命题秉持素养立意，多以策略性知识为背景，考查学生必备知识、关键能力、学科素养和核心价值，就数学而言最核心的价值就是发展学生的数学素养和提高解决问题的能力.数学名家说过，问题是数学的心脏，思维是数学的灵魂，而方法则是数学的行为，从一个经典的，简明的数学问题出发，把数学冰冷的美丽转化成数学火热的思考.通过多角度，全方位的观察、感知、分析、尝试、提炼、综合，使得数学的思考从联系、到联通，再到思维的有效对接，能够很好地优化解题思路，提升分析问题解决问题的能力.近几年解析几何在高考中对计算能力的考查逐年加大，而好的解法能够简化运算，所以在平时教学中要注重一题多解在解析几何中的应用，可以从不同的角度去思考和分析问题，在多种解法中去寻求通解和优解.

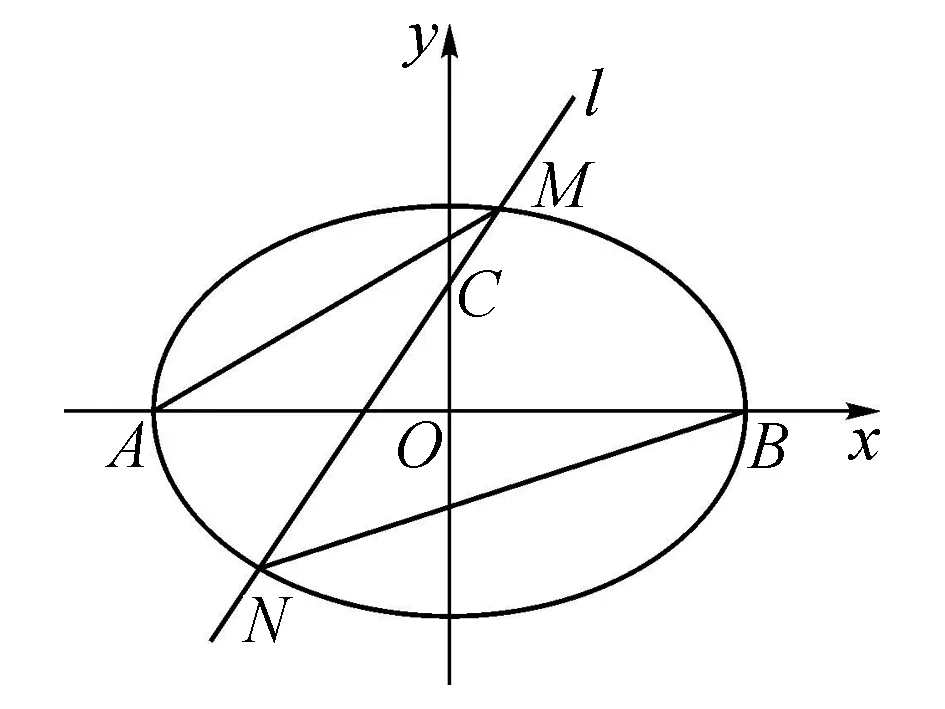
(1) 求椭圆C的标准方程；

(2) 如图，过点C(0，1)且斜率大于1的直线l与椭圆交于M，N两点，记直线AM的斜率为k1，直线BN的斜率为k2，若k1=2k2，求直线l斜率的值.

分析(1)根据已知条件，建立方程组，求出a，b，即可得到椭圆的标准方程.

(2)设出直线l方程为y=kx+1，M(x1，y1)，N(x2，y2)，将直线l方程与椭圆方程联立，求出x1+x2和x1x2，根据条件求出k1和k2，代入k1=2k2化简计算，得到关于k的方程，解方程求出k的值.

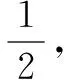
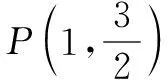
(2)解法一(通过两边平方转化成韦达定理形式)

由椭圆的对称性可知直线l的斜率一定存在，设其方程为y=kx+1.

设M(x1，y1)，N(x2，y2).

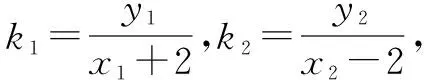
又因为M(x1，y1)，N(x2，y2)在椭圆上，

即3x1x2+10(x1+x2)+12=0.

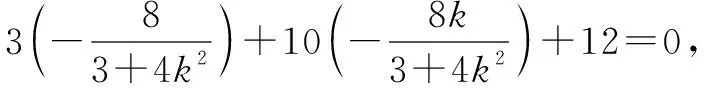
解法二(通解)

由椭圆的对称性可知直线l的斜率一定存在，设其方程为y=kx+1.

设M(x1，y1)，N(x2，y2).

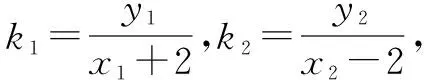
kx1x2+(2k+2)(x1+x2)+(2k-3)x2+6=0,

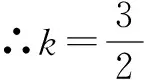
2(kx1+1)(kx2+1)=-3(x1+2)(x2+2),

(2k2+3)x1x2+(2k+6)(x1+x2)+14=0.

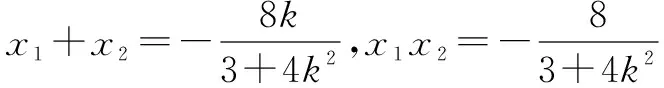
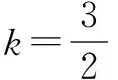
解法四(将直线AM与椭圆方程联立，解出M、N)