线性规划问题的求解策略
吴维峰
(山东省青州市潍坊工程职业学院 262500)
一、最值问题

A.2 B.3 C.5 D.6
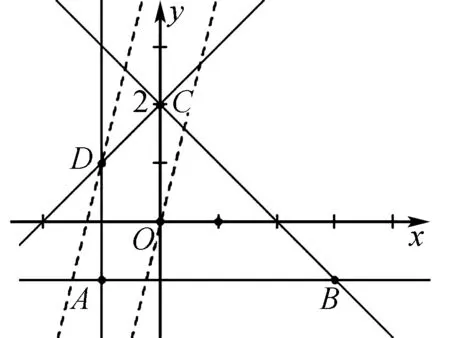
图1

结合图象,可知目标函数z=-4x+y取得最大值的(x,y)是两直线x-y+2=0与x=-1的交点D(-1,1),此时z=-4×(-1)+1=5,故答案:C.
点评破解此类在约束条件下目标函数的最值的线性规划问题,关键是根据题目条件作出约束条件所对应的可行域,利用图象在可行域所对应的平面区域下找出决策变量使得目标函数达到最值时的点,结合两直线的交点的求解并代入目标函数来确定相应的最值问题.
二、参数问题

A.3 B.2 C.-2 D.-3
分析根据条件作出相应的可行域,结合图象,利用对应直线族中斜率-a的取值情况加以分类讨论,结合截距的最大值来建立关系工,从而得以确定参数值问题.

图2

当z取得最大值4时满足条件,但直线要与可行域相交,当0<-a≤1时,即-1≤a<0时,以及当-1≤-a<0时,即0 ①根据河道整治工程的实际需要,工程单位需要做好防汛防台工作,并制定出专项的预防方案。②基于汛期的到来,工程单位要做好施工围堰工作,并组织专门人员勘测围堰,主要检查其是否存在渗水的现象。③做好基坑排水设施。及时对基坑排水系统进行疏通,确保排水系统能够稳定运行,发挥排水系统的作用,及时将积水排除基坑。④加强对排水沟建筑物通畅情况进行全面检查,并组织专门人员对其进行检查,一旦发现堵塞的地方,则需要及时对其进行疏通。 当-a>1时,即a<-1时,结合图象,可知此时最优解为O(0,0),此时zmax=0,不合题意; 当-a<-1时,即a>1时,结合图象,可知此时最优解为A(2,0),此时zmax=2a+0=4,解得a=2. 综上分析可得a=2,故选择答案:B. 点评破解此类在约束条件下相关参数求值或取值范围的线性规划问题,根据参数所在的位置(约束条件或目标函数),若在约束条件中,利用目标函数的相关信息来确定约束条件所对应的大致可行域,进而得以处理;若在目标函数中,利用直线的斜率的取值情况加以分类讨论,从而得以破解. 分析根据条件作出相应的可行域,并分别求解平面区域所对应的三角形的三个顶点坐标以及相应的截距值,结合z=y-ax取得最大值的最优解不唯一来确定对应截距值之间的关系,从而得以分析与求解. 图3 点评破解此类在约束条件下相应的最优解的线性规划问题,关键是根据题目条件作出约束条件所对应的可行域,则在封闭区间中最优解有无数组时,其对应的目标函数的直线与可行域中的对应边平行即可,从而得以数形结合,合理转化. 下面给出了四个命题:①pq;②pq;③pq;④pq. 这四个命题中,所有真命题的编号是( ) A.①③ B.①② C.②③ D.③④ 分析根据条件作出相应的可行域,利用相关命题并结合特殊点的坐标来判定其真假,再利用复合命题的性质来判断各相关复合命题的真假情况,从而得以正确判定. 图4 点评破解此类在约束条件下与其他知识交汇的综合的线性规划问题,关键是根据题目条件作出约束条件所对应的可行域,综合其他知识加以合理分析与综合,多知识交汇,综合来解决相关问题.三、最优解问题
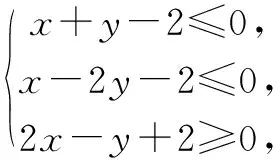
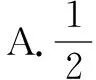


四、综合问题