一道高中数学联赛预赛试题的探究与思考

张晓建

(安徽省滁州中学 239000)

(1)求椭圆C的方程；

(2)E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线E,F的斜率为定值.并求出这个定值.

文[1]给本题进行了推广和类比得到了如下的结论：

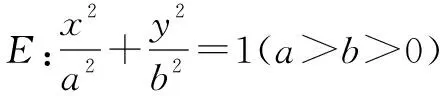
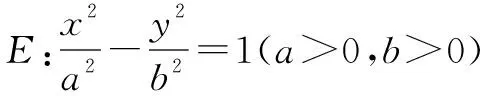
在笔者看来上述结论是否可以认为过圆锥曲线上一点P(x0,y0)(y0≠0)作两条关于x=x0对称的两条直线l1,l2与圆锥曲线分别交于A,B两点，则随l1,l2变化可以得到一组平行直线. 无独有偶，在2019年全国高中数学联赛广西省预赛的第11题引起了笔者的注意.

一、问题呈现

(1)求k·k1的值；

(2)求证：对任意k，直线MN过定点.

该问题是过椭圆短轴端点的一条直线，过此端点作两条关于这条直线对称的直线，与椭圆分别交于M,N，直线MN过定点的问题.和2009年辽宁高考试题比较，两道试题背景相同，那么这个问题是否可以推广到一般情形呢？具有怎么样的规律呢？笔者做了大胆的尝试，得到了一些有意思的结论.

二、探究延伸 得出结论

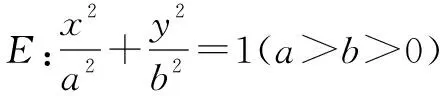
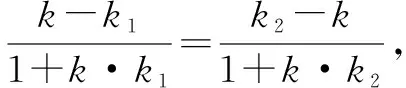
即：(k-k1)(1+k·k2)=(k2-k)(1+k·k1)，

化简可得：(k1+k2)(1-k2)=2k(1-k1·k2)(*).

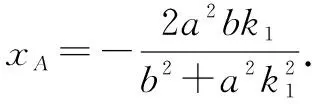
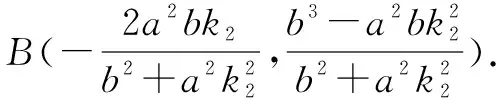
直线AB的斜率为

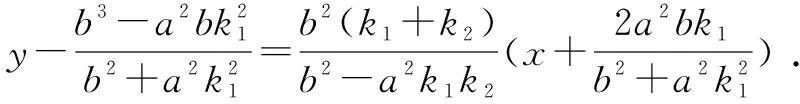
即(b2-a2k1k2)y=b2(k1+k2)x+b(b2+a2k1k2).

化简得到：b2(k2-1)y+2b2kx-b3(k2-1)=k1k2[a2(k2-1)y+2b2kx+a2b(k2-1)].

上式对于任意k1,k2都成立，故有：

特别地，当直线过椭圆长轴端点时我们可以得到如下结论：

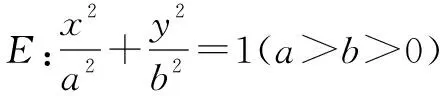
三、横向推广

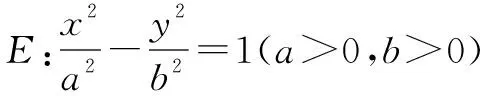
其证明与结论4证明相似.同样在抛物线中我们也得到如下结论：

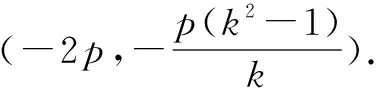
证明抛物线中：l1：y=k1x与直线l2：y=k2x关于直线l：y=kx对称，(*)式依然成立.

(2ky-(k2-1)x)k1k2=2ky+2p(k2-1).

上式对于任意k1,k2都成立，故有：

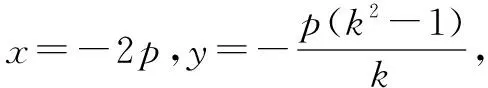
本次问题的探究结果可谓是让人惊叹不已，同一个背景的问题恰是两种不同的结果，一个是定值问题，一个是定点问题，定值问题是定点问题的特殊情形.同时该题的探究体现圆锥曲线完美的统一性质，在研究的过程中借助了几何画板软件观察定点结果，在推广的过程中也凸显了数学的核心素养，对数学直观、数学抽象、逻辑推理、数学运算有着深刻的理解.

当然本题也可以继续思考：圆锥曲线上的点是否可以是任意点，而不在顶点呢？这个问题还需要继续探究，希望有兴趣的读者一起继续探究，感受数学之美.