高中数学解决函数零点个数问题的解答方法

薛 婷

(山东省枣庄市第三中学 277000)

在练习题目当中出现的函数零点问题，大部分都是要考查学生的函数与方程思想的掌握程度，遇到这一类题型，不仅要求学生要研究函数的单一性，同时也要考虑到零点存在定理，要确保解的个数的充要性.这是同学们在解决这一问题是必须要考虑的条件，也是保证解题正确的一个重要前提.

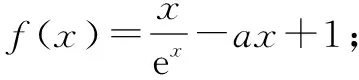
(1)当a=1时，求y=f(x)在区间x∈[-1,1]上的值域.

(2)试着求出函数f(x)的零点的个数，并证明你的结论是否正确.

分析遇到这样的问题，我们首先应该对题目当中给出的函数的单调性、最大值、最小值、变化趋势等内容进行分析，然后再借助这个函数的大致图象来判断零点的情况.

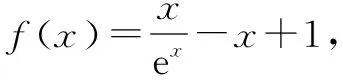
当x∈(0,1)时，f′(x)<0，f(x)递减.

所以当x=0时，f(x)取得极大值，也是函数f(x)的最大值，即f(x)max=f(0)=1.而f(x)min={f(-1),f(1)}min=f(-1)=2-e.所以，f(x)在区间x∈[-1,1]上的值域为[2-e,1]

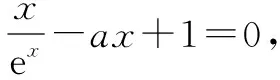
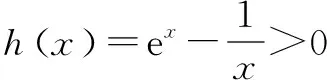
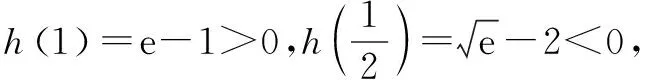
②若a<0，则

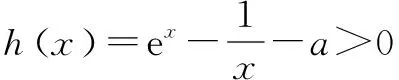
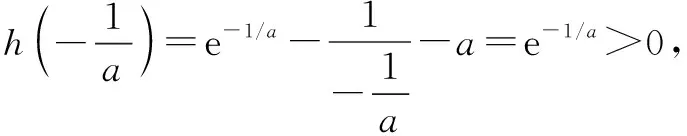
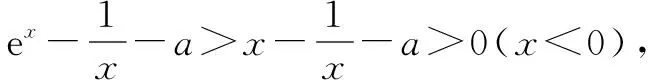
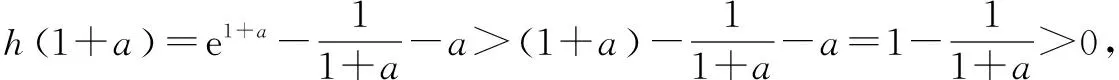
在上面的这道例题当中，第一小问在求解值域问题时，我们一定要注意对函数求导，并且对导数的范围进行讨论，这是一个必须的过程，能够保证解题的准确性.而这道题目当中的第二小问与第一小问没有必然的联系，同学们在求解的过程中，一定要记住不能把第一小问当中题目给出的已知条件带入到第二小问中进行运算，那样是不正确的.求解零点问题需要我们对题目进行分类讨论，在这道例题当中，由于原函数当中存在一个未知量a，所以我们要对未知量的取值进行分类讨论，仍然要对函数进行求导，并且研究函数和导函数的基本性质.在解题的过程中，我们应该尽可能的保持书写的整齐，这样一来既能够保持卷面的美观，也能让我们在后续进行检查的时候，能更加清晰地对自己的解题步骤进行归纳和检验.