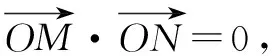动中寻“静” “定”题有招

陈国林

(江西省南昌市东华理工大学理学院 330013)

在新课程的标准要求下，平面解析几何问题对数形结合思想要求较高，以坐标法为核心，通过建立曲线方程，考查相关性质.这类试题的命制知识综合性较强，能够考查学生的逻辑思维，数学运算的能力.其中对于圆锥曲线中的定点、定值问题，要从题目信息中，以“静”寻“定”，依据题目条件，挖掘“定”题绝招.下面通过具体实例进行分析.

一、过定点问题

直线或曲线过定点问题需要把直线或曲线方程中的变量x，y视为常数看待，通过把方程一端化为零，且这个方程需要对任意参数都成立，所以这时的参数系数就要全部等于零，就可以得到一个关于x，y的方程组，这个方程组的解所确定的点就是直线或曲线所过的定点.

1.直线过定点

(1)求点P的轨迹C的方程；

(2)过点M(1，2)作曲线C的两条弦MA，MB，设MA，MB所在直线的斜率分别为k1，k2，当k1，k2变化且满足k1+k2=-1时，证明直线AB恒过定点，并求出该定点坐标.

评注该题可以通过代数推理，通过设出未知点的坐标，将直线MA、MB的方程表示出来后，利用根与系数的关系，直线方程的两点式即可写出AB的直线方程，最后利用直线系方程的知识即可求出直线AB经过的定点.

2.曲线过定点

(1)求a，b的值，并写出椭圆C的方程；

(2)设A，B分别为椭圆C的左、右顶点，在椭圆C上有异于A，B的动点P，若直线PA，PB与直线l:x=m(m为常数)分别交于不同的两点M，N，则当点P运动时，以MN为直径的圆是否经过定点？

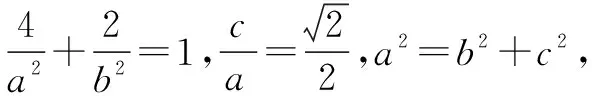
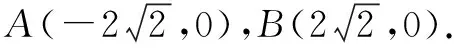
点评解决圆锥曲线中有关曲线恒过定点问题时，需要细心挖掘题目信息，将所求曲线表示出来.本题是圆过定点问题，解决此类问题，通过确定圆的圆心坐标和半径后，依据圆的标准方程即可以求出圆恒过的定点值.

二、定值问题

解析几何中的定值问题是指某些几何量，例如线段的长度、图形的面积、直线的斜率、角度的大小或某些代数表达式的值等和题目中的参数无关,不依参数的变化而变化,而始终是一个确定的值.

1.直线斜率为定值

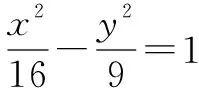
(1)求椭圆的标准方程；

(2)若E，F是椭圆上关于原点对称的两点，P是椭圆上一点，则当直线PE，PF的斜率都存在，记为kPE，kPF，则kPE·kPF是否为定值？若是，求出这个定值；若不是，请说明理由.

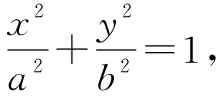
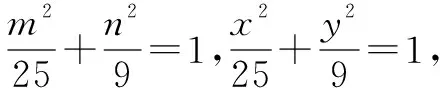
点评直线斜率是否为定值问题，毋庸置疑需要先将直线的斜率表示出来，通过已知条件列出方程，再进行化简即可得出定值.

2.面积为定值

(1)求椭圆C的方程；

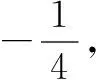
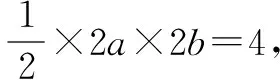
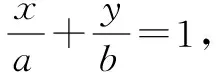
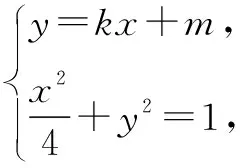
综上可知，△OMN的面积为定值1.

三、线段长度为定值

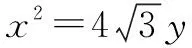
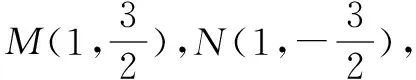
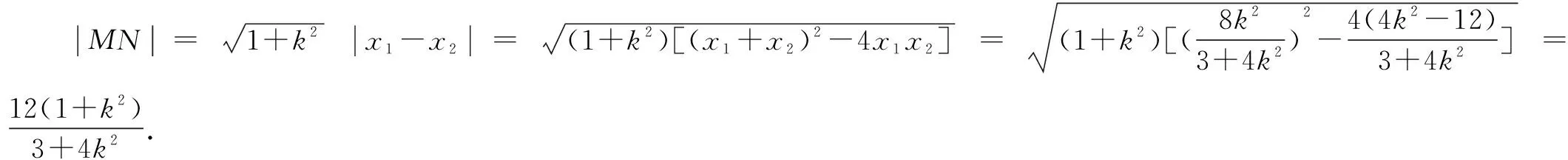
点评求解解析几何中的线段长度或比值为定值问题时，需要利用弦长公式、勾股定理，点到直线间的距离等相关公式求解出各线段长度的表达式，再将其比值表示出来，通过变形化简，即可确定线段长度的比值.

四、角度为定值

(1)求抛物线C的方程；

(2)若点E在抛物线C上，且纵坐标为2，经过点(2，0)的直线l与抛物线C交于A，B两点(不同于点E)，直线EA，EB分别交直线x=-2于点M，N，O为原点，求证：∠MON为定值.

(2)易知点E(2，2).设直线l:y=k(x-2)与抛物线C交于A(x1，y1)，B(x2，y2)两点.