基于EEMD的滚动轴承故障诊断方法

季景方，吴宣霖，黄瑞琛

（湖北汽车工业学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰442002）

滚动轴承具有效率高、摩擦阻力小、装配方便、润滑容易实现等优点，因而在旋转机械中得到广泛应用，是大部分旋转机械的基本组成部件。滚动轴承是易损零件，许多旋转机械中的故障都与滚动轴承有关。研究在滚动轴承不停机状态下进行实时信号采集和故障诊断对降低经济损失、避免重大事故发生的意义重大。陶栩通过对实测振动信号进行EMD，选择比较大的峭度值来筛选IMF 分量达到提取滚动轴承故障频率的目的［1］。罗金等提出了基于EEMD 和堆叠稀疏自编码的滚动轴承诊断方法，有效解决了智能诊断方法训练时间长、识别率不高的问题［2］。张树等采用细菌觅食算法对传统变分模态分解参数进行优化使得变分模态分解算法对轴承故障诊断解析效果更高，对故障的敏感性和抗噪能力更强［3］。De Jie Yu 等基于EMD 和Hillbert 谱提出了滚动轴承故障诊断的新方法，同时以外圈故障和内圈故障为例验证了所提出方法的有效性［4］。EMD 存在模态混叠、端点效应，同时单一采用峭度值进行故障诊断具有故障诊断精度不高的问题。基于此，文中采用EEMD对实测滚动轴承故障信号进行分解，联合相关系数和峭度值双准则来选择有用的IMF分量，从而达到对滚动轴承故障进行诊断的目的。

1 EMD及EEMD算法

1.1 EMD算法

EMD 是Huang 等人从瞬时频率的角度出发提出的新信号处理方法，通过EMD 将信号中存在的不同尺度的波动分解出来，从而形成一系列具有不同特征尺度的数据序列，这些不同特征尺度的数据序列称为本征模态函数（IMF）。对于信号x(t)，EMD过程如下［5］：

1）确定信号x(t)中的所有局部极大值和极小值点，采用三次样条函数将所有的局部极大值和极小值点连接起来形成上下包络线，计算上下包络线的平均值m1。

2）将信号x(t)减去上下包络线均值m1，那么可以得到新的序列h1：

5）将r1作为原始数据，重复步骤1）～4）得到第2个IMF分量c2。

6）不断地重复步骤1）～5）n次，那么就可以得到原始信号x(t)的n个IMF 分量，此时rn为单调函数，无法继续提取IMF分量。

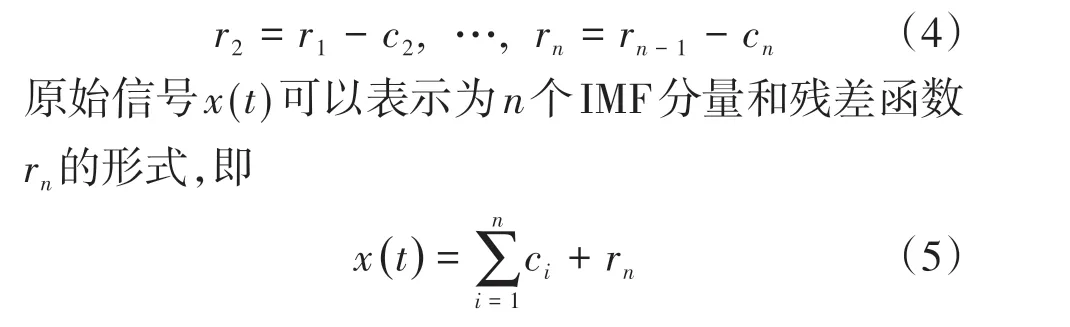
1.2 EEMD算法

EMD 对处理非线性、非平稳信号中具有十分广泛的应用，但是存在模态混叠、端点效应，在很大程度上影响了信号分解的准确率和故障特征提取的效率。针对EMD 存在的模态混叠现象，EEMD（集合经验模态分解）对EMD 进行了改进，使得不同时间尺度的信号自动分离到和其相适应的参考尺度［6］。EEMD 是在原始的信号中添加均匀分布的白噪声，使得信号变得集中、连续，提供了噪声对信号的干扰，削弱了瞬时冲击对信号分解所产生的影响。对于信号x(t)，EEMD过程如下［7］：

1）在信号x(t)中施加白噪声，将包含白噪声的信号进行EMD，得到各阶IMF分量；

2）重复将不同的白噪声加入原始信号x(t)中，同时进行EMD，得到各阶IMF分量；

3）将每次EMD 得到的IMF 分量进行加权平均，最终得到EEMD的分解结果。

采用EEMD的过程中，白噪声起辅助作用。实验表明，添加白噪声的次数为50～100 次所得到的EEMD 效果最好。相对于EMD，EEMD 使得EMD中存在的模态混叠现象和虚假模态分量有效减少。

2 滚动轴承故障诊断方法

2.1 相关系数

由于实测振动信号中含有噪声，滚动轴承的故障往往被淹没在噪声中。对实测的振动信号进行EEMD，通过计算IMF分量和原始振动信号之间的相关系数可以筛选出哪些IMF分量是真实的IMF分量，哪些IMF分量是虚假IMF分量。实测振动信号和各阶IMF分量之间的相关系数ρ计算公式为

对于真实的IMF分量，其相关系数比较大；对于虚假的IMF分量，其相关系数比较小。

2.2 峭度

峭度是描述波形尖峰度的无量纲参数，对于信号中存在的瞬时冲击特征非常敏感，因此广泛应用于滚动轴承的故障诊断中。峭度K计算公式为

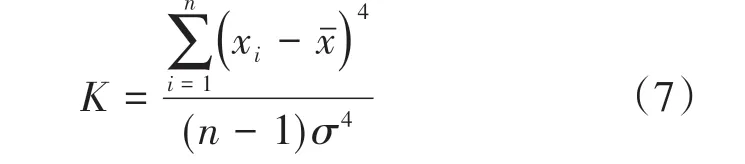
式中：xˉ为均值；σ为标准差。如果滚动轴承正常运转，那么测试所得振动信号趋于正态分布，K值约为3；如果滚动轴承出现故障，那么测试所得振动信号某时段的K值大于3。峭度值越大，测试所得振动信号中包含的故障冲击成分越明显［8］。

2.3 轴承故障诊断流程

对实测的滚动轴承振动信号进行EEMD，计算EEMD 所得的各阶IMF 分量和原始振动信号的相关系数以及各阶IMF 分量的峭度值。通过分析相关系数值和峭度值来选择有效的IMF分量，对信号进行重构处理。对重构后的信号进行Hillbert包络解调，得到重构后信号解调谱，在解调谱中寻找特征频率［9］。滚动轴承故障诊断流程如图1所示。

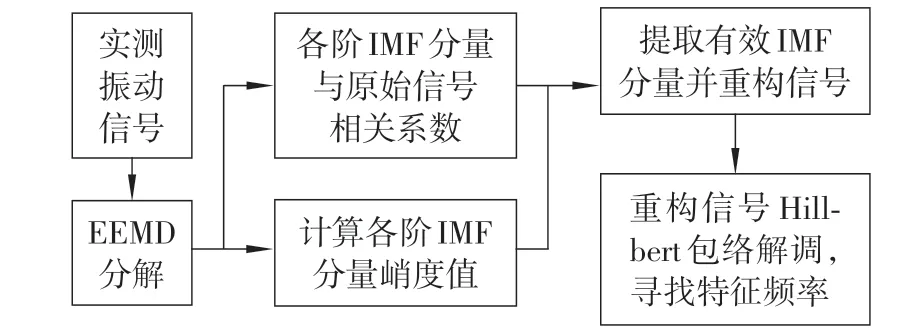
图1 滚动轴承故障诊断流程

3 实例分析

3.1 试验数据

试验数据来自美国西储大学滚动轴承研究中心的电气工程实验室，选择6203-2RSJEMSKF深沟球轴承，内圈直径为25 mm，外圈直径为52 mm，厚度为15 mm，滚动体直径为7.94 mm，滚道节径为39.04 mm，接触角为0°，滚动体个数为9。不同类型的故障有不同的特征频率计算公式。滚动轴承内圈故障和外圈故障的特征频率计算公式如式（8）～（9）所示［10］:

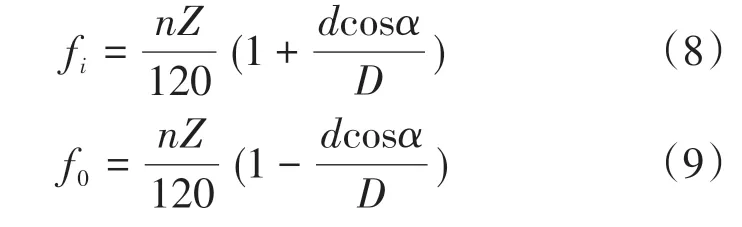
式中：n为转速；Z为滚动体个数；d为滚动体直径；α为接触角；D为轴承节圆直径。按照式（8）～（9）可以得到滚动轴承内圈故障频率为157.5 Hz，外圈故障频率为105 Hz。采用加速度传感器进行滚动轴承振动信号数据采集，试验采用频率为12 kHz。图2为美国西储大学轴承试验台。

图2 美国西储大学轴承试验台

3.2 数据处理和分析

3.2.1 滚动轴承内圈故障数据处理和分析

通过试验测得滚动轴承内圈故障的时域波形图，对其进行Hillbert包络解调，得到解调谱，如图3所示。由图3 可见，直接对实测信号进行Hillbert变换提取滚动轴承内圈特征频率，其解调谱中干扰比较多，无关的频率成分峰值也比较大，滚动轴承内圈故障特征频率无法提取。对实测的滚动轴承内圈故障时域信号进行EEMD，计算得各阶IMF分量和原始信号的相关系数以及各阶IMF 分量的峭度值，结果如表1所示。

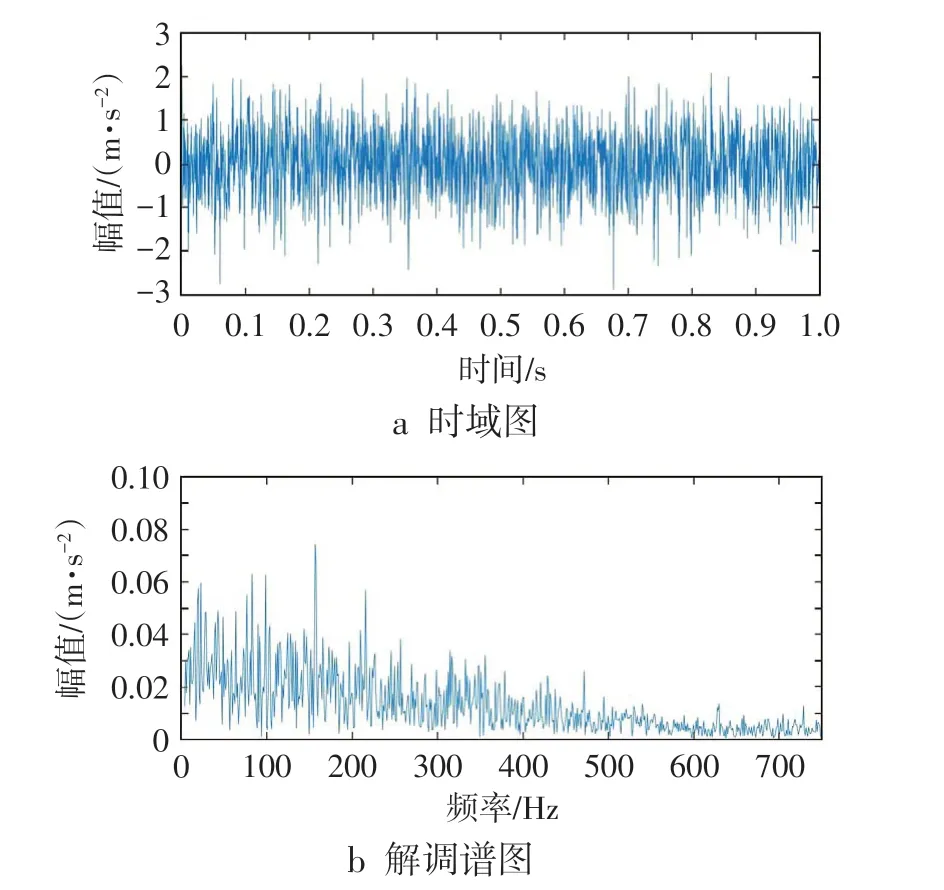
图3 滚动轴承内圈故障时域和解调谱图

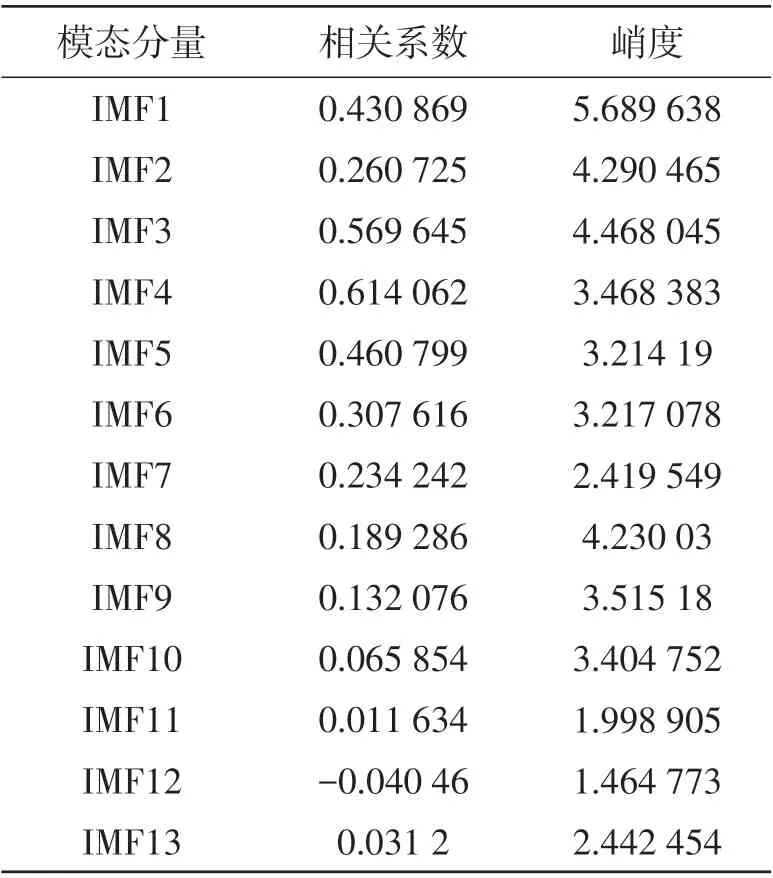
表1 滚动轴承内圈IMF分量相关系数与峭度

对有效IMF 分量的选择关系到故障诊断的精度，一般要综合考虑相关系数和峭度，选择相关系数和峭度值均比较大的IMF 分量。由表1 可见，IMF1、IMF3、IMF4 和IMF5 的相关系数和峭度均比较大，因此可以选择IMF1、IMF3、IMF4 和IMF5 作为有效IMF分量进行信号重构，得到第1个重构信号，对重构后的信号进行Hillbert包络解调，得到解调谱，如图4a所示。从峭度的角度来讲，如果滚动轴承正常运转，那么测试所得振动信号趋于正态分布，峭度值约为3，与IMF4和IMF5的峭度值差别不大，因此选择IMF1和IMF3作为有效IMF分量进行信号重构，得到第2 个重构信号，对重构后的信号进行Hillbert 包络解调，得到解调谱，如图4b所示。对比图4a和图4b，选择IMF1和IMF3作为有效IMF分量来进行信号重构，对滚动轴承内圈故障特征频率提取效果比较好，同时也可以节省计算的成本。

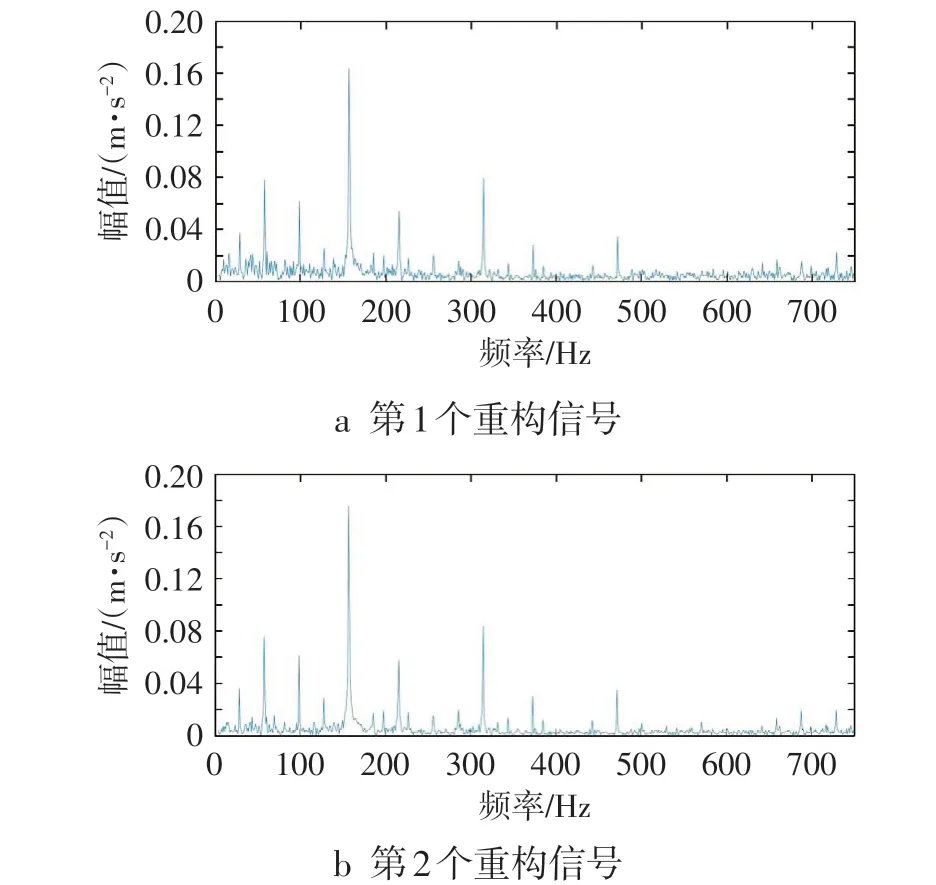
图4 滚动轴承内圈重构信号解调谱图

3.2.2 滚动轴承外圈故障数据处理和分析

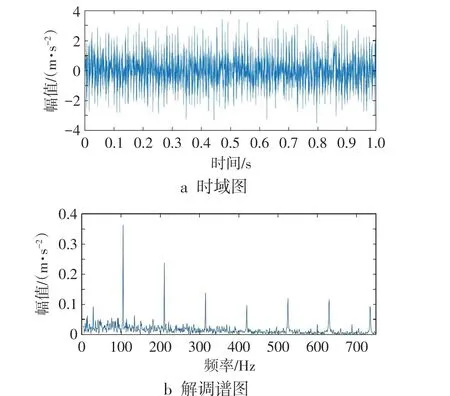
图5 滚动轴承外圈故障时域和解调谱图

通过试验测得滚动轴承外圈故障的时域波形图，对其进行Hillbert包络解调，得到解调谱，如图5所示。由图5 可见，直接对实测信号进行Hillbert变换提取滚动轴承外圈故障特征频率，尽管外圈故障特征频率可以提取，但是干扰比较多，无关的频率成分峰值也比较大，对滚动轴承故障特征的识别有比较大的干扰。对实测的滚动轴承外圈故障时域信号进行EEMD，计算得各阶IMF分量和原始信号的相关系数以及各阶IMF分量的峭度值，结果如表2所示。

选择IMF1、IMF3和IMF4作为有效IMF分量进行信号重构，得到第1 个重构信号，对重构后的信号进行Hillbert 包络解调，得到解调谱，如图6a 所示。选择IMF1 和IMF3 作为有效IMF 分量进行信号重构，得到第2 个重构信号，对重构后的信号进行Hillbert 包络解调，得到解调谱，如图6b 所示。对比图6a和图6b，选择IMF1和IMF3作为有效IMF分量来进行信号重构，对滚动轴承外圈故障特征频率提取效果比较好，同时也可以节省计算的成本。

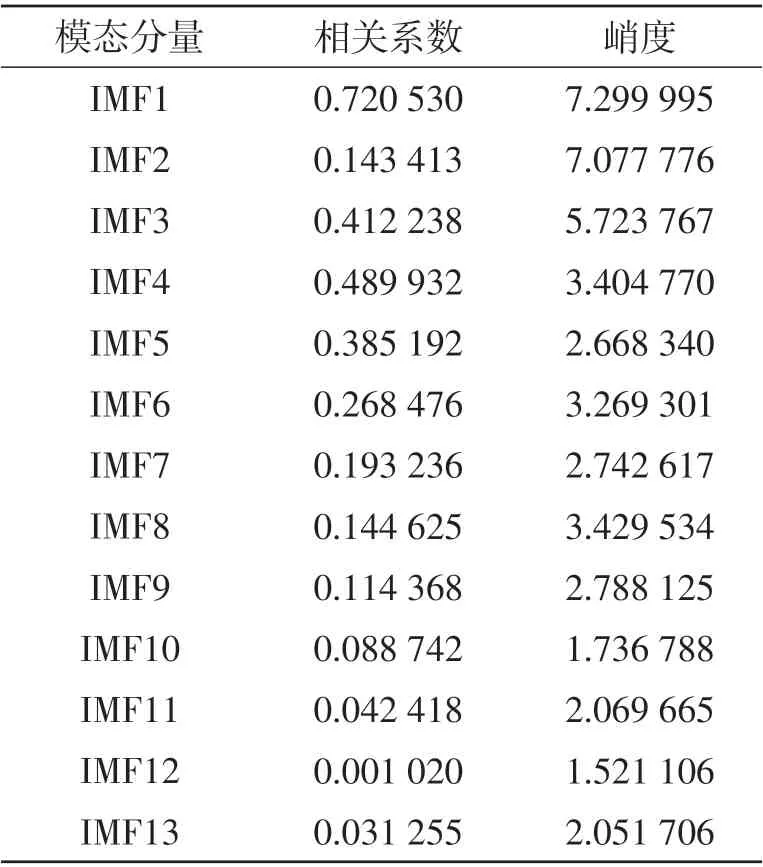
表2 滚动轴承外圈IMF分量相关系数与峭度

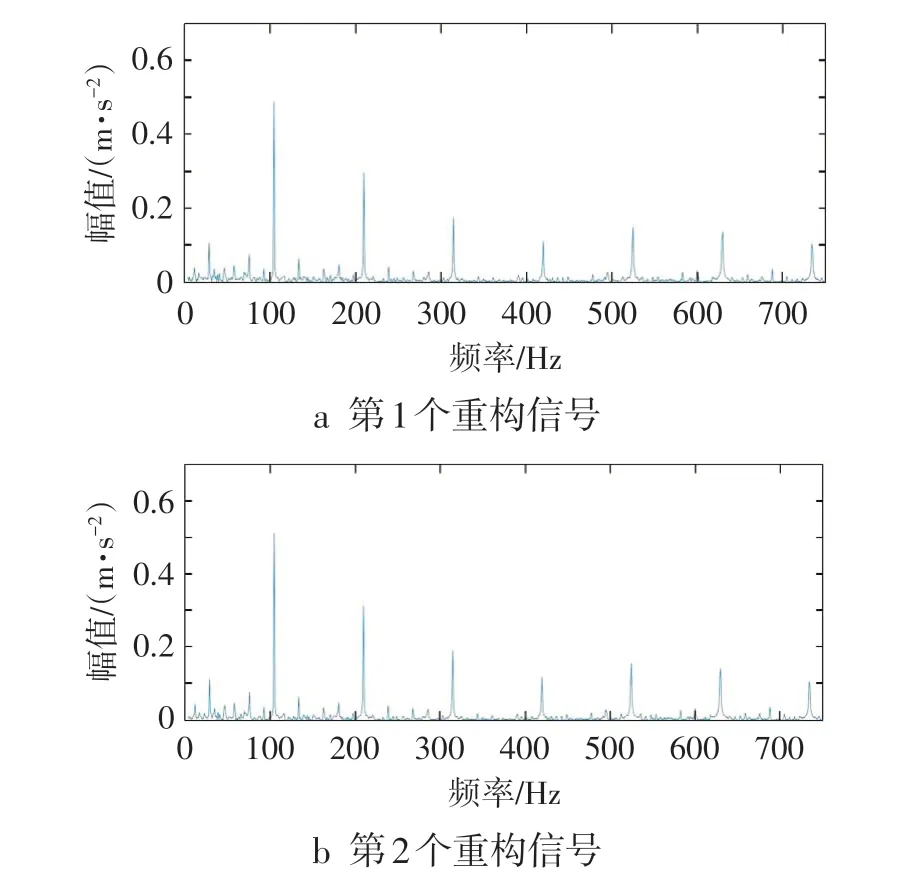
图6 轴承外圈重构信号解调谱图

4 结论

针对EMD 存在的模态混叠、端点效应，采用EEMD对实测振动信号进行分解，联合相关系数准则和峭度准则给出滚动轴承故障诊断的新方法。通过对实测滚动轴承内圈故障和外圈故障振动信号的分析，得出以下结论：1）联合相关系数准则和峭度准则选择有用的IMF分量对信号进行重构，对重构后的信号进行Hillbert包络解调得到的解调谱可以有效地识别故障特征频率；2）对有用IMF分量选择时优先考虑峭度，一般峭度值要大于3.5，同时相关系数大于0.4，其提取的IMF 分量抗噪能力更强，为有效IMF分量选择提供了参考。