一元线性回归参数的估计

李秀兰

（山西大同大学数学与统计学院，山西大同 037009）

变量间常见的关系有两类：一类是确定性关系，这些变量间的关系是确定的，给定x的值，y的值唯一确定，可以用函数y=f(x)表示；另一类是相关关系，变量间有关系，但是不能用函数表示，也就是说，给定x的值，y的值不唯一确定。回归分析就是研究变量间的相关关系的一门学科，它通过对客观事物中变量的大量的观察或试验获得的数据，去寻找隐藏在数据后面的相关关系，给出表达形式——回归方程的估计[1-2]。

一元线性回归的模型为

其中β0,β1,σ2未知参数,x是普通变量。

给定x的值xi,对y进行观测,得y的值yi,i=1,…,n。

由数据对(xi,yi)估计出β0,β1,记为则可得y与x关系的一个估计

称上式为回归方程(经验回归函数),称其图像为回归直线。

1 回归系数的点估计

(1)最小二乘估计。

在x=xi处,y的实际值yi与回归值的差异为=yi-β0-β1xi，令

Q(β0,β1)=应该满足

引入记号

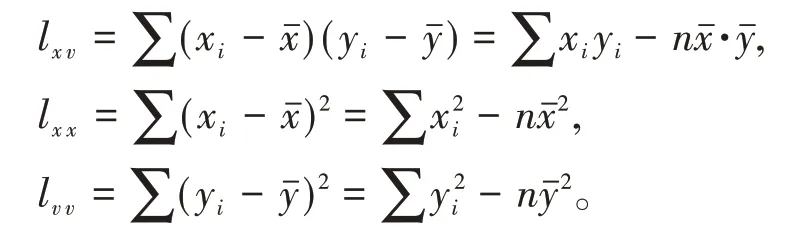
对β0,β1求偏导并令其为0，得正规方程组

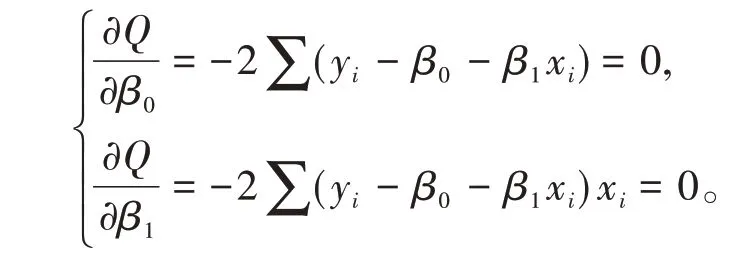
整理得

解方程组得

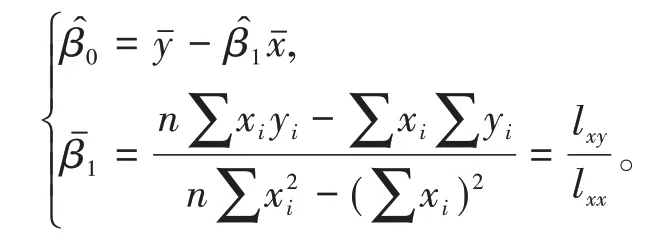
(2)回归系数的最大似然估计。

似然函数为

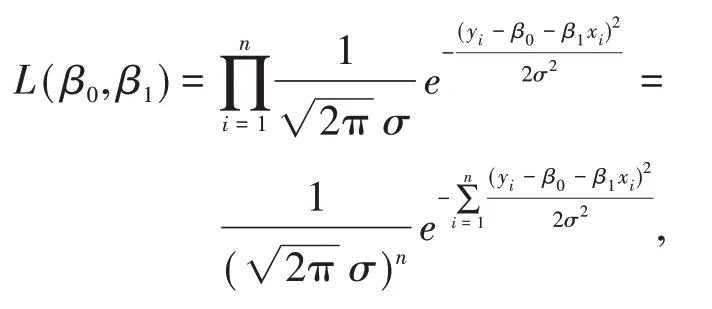
两边取对数得

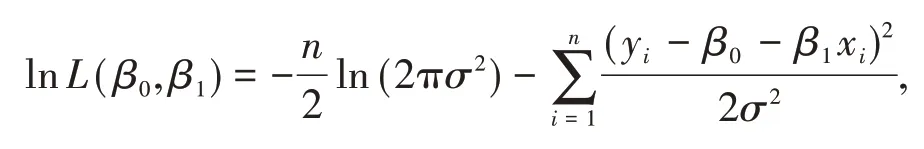
对β0,β1,σ2求偏导并令其为0，得

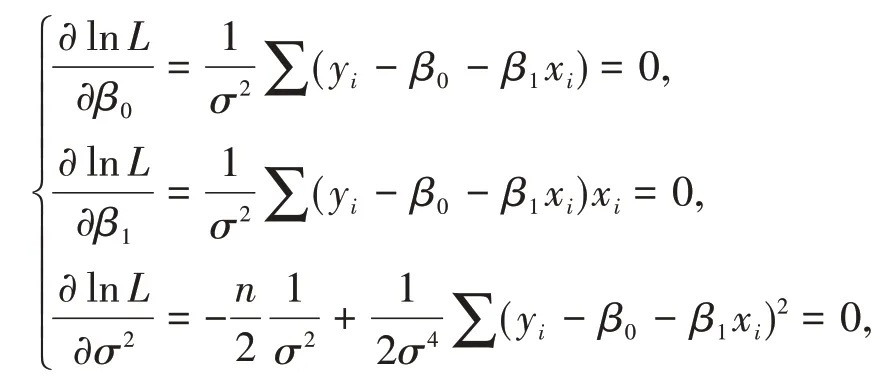
解方程组得

可以看到在随机误差服从正态分布时，参数的最小二乘估计与最大似然估计一致的，但是如果不知道随机误差的分布时，最小二乘估计还与上面的结果相同，但此时不能求最大似然估计。

2 回归系数的区间估计

引理1设yi=β0+β1xi+εi,i=1,2,…,n,εi～N(0,σ2),各εi间独立，则

显然Se/(n-2)是σ2的无偏估计;

为了得到β0,β1的区间估计，可以考虑t分布枢轴量

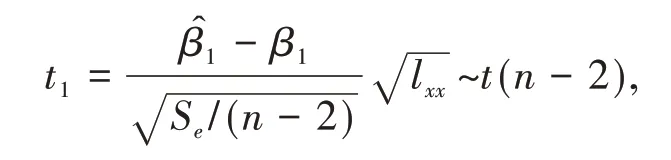
对于给定的置信水平1-α，查表得t1-α/2(n-2)，从而可以得到β0的置信区间是

对于给定的置信水平1-α，查表得F1-α(1,n-2)，从而可以得到β0的置信区间是