基于上证50指数的Smart Beta及CPPI类综合策略研究

牛晓健，李雅馨

（复旦大学 经济学院，上海 200433）

一、引言

近年来，Smart Beta策略成为量化投资领域的研究热点。从2000年第一只Smart Beta基金被发布以来，世界Smart Beta市场逐渐走向繁荣，相关产品规模成长迅速。Smart Beta策略指数不同于传统的风格指数，因为前者通常会通过相对量化、透明的规则求解最优化权重，而后者通常为应用市值进行加权（Hsu，2014［1］）；Smart Beta指策略也存在显著不同，Smart Beta指策略通常根据成分股对因子的暴露情况决定权重，具有透明、基于历史数据的特点，而Al ph a策略通常投资于相对广泛的范围，多基于投资经理对未来表现的预测性判断（Jacobs&Levy，1988［2］）。

目前Smart Beta指数并没有一个统一的定义。赖淼华（2017）［3］认为，广义Smart Beta指数是指基于规则或量化的方法，与传统市值加权成分股在成分选择或权重决定方式方面差异的指数，包括各类风格指数及策略指数、非市值加权的指数等，其旨在通过增加指数在某些风险因子上的暴露获取相应的超额收益；晨星（Morning S tar）采用了类似定义，并将Smart Beta指数大致分成三类：

（1）收益增强类：单因子策略指数（如价值、成长、动量、质量等）、多因子策略指数及基本面指数（通过红利、净利润、收入等指标决定权重）等。

（2）风险分散类：风险加权指数，如等权重指数、最小方差指数、风险平价指数、最大分散化指数等。

（3）其他类：多资产指数，非传统商品、债券指数等。

虽然目前Smart Beta策略在海外成为投资新宠，各类学术研究、商业研报层出不穷，在中国，Smart Beta策略的研究及应用仍处于较为初级的发展阶段，相关产品及学术研究仍相对匮乏。截至2018年年末，中国的Smart Beta产品仅有78只，规模不足380亿元，在ETP中占比不足10%，与美国Smart Beta产品7 862亿元的规模相差巨大，可以预计未来还有较大的发展空间。同时，随着国内2018年Smart Beta产品发行速度加快，预计Smart Beta产品在中国将会迎来快速发展期，具有较为良好的发展前景。

美国人寿保险业于20世纪80年代中期设立了保本基金，这也是金融界保本基金的开端。保本基金采取的技术方法主要为基于期权的投资组合策略（Option-b ased Portfolio Insurance，OBPI）及固定比例投资组合保险策略（Constant Proportion Portfolio Insurance，CPPI）两种。OBPI策略的构建基于期权，该策略通过综合使用股票及其相对应的看跌期权，来达到保本的目标。CPPI策略一般设置投资周期，通过动态调整投资组合在风险资产及无风险资产间的资产配置比例，保证组合的最大回撤可控，这一比例也被称为本金保护比例或要保额度。CPPI策略作为保本策略的一种，由于其具有简单、在机制上可实现保本的特点，在投资中也较为流行，较多应用于对冲基金、零售产品、寿险产品等。

但简单的CPPI策略可能过于僵化，在收益较多时存在忽略市场波动情况、无法满足投资者存在对保留投资组合在演变过程中的最高价值的需求等问题，因此可以对CPPI策略进行改进（杨辉平，2014［4］）。非时变的资产组合保护策略（Time-invariantPortfolio Protection，TIPP）能够动态调整期末保证的资金比例，将组合的保本底线从本金一定比例调整为本金的一定比例与资产组合曾达到的最高价值的一定比例的最大值，从而不断上调组合的目标保本价值，因此能够更好地满足投资者的投资需求。目前国内保本基金通常采用CPPI策略，部分采用TIPP策略，在市场大幅震荡期间，保本基金由于其本金保证的特点更受人青睐。

近年来，全球局势震荡加剧，全球股市的系统性风险上升，中国A股市场整体的波动性也有所增强。虽然基于风险类的Smart Beta策略相较其他单因子、多因子策略可以通过优化个股权重更好地控制组合风险、实现较高的夏普比率，但当整体市场出现下行时，投资组合仍将面临较大的亏损风险；而CPPI类策略作为投资组合保本策略，关注对资产组合本金的保护，从理论机制上来说，无论市场环境的恶劣程度如何，均可达到保证组合安全性目标。因此，基于两种策略的不同特点，如果综合使用两类策略，可能能够博采众长、综合利用两者的优点，在实现超额收益的同时有效规避市场大幅下行风险，达到更好的投资效果。

有基于此，本文将考虑综合使用两类策略，将利用风险分散类方法生成的Smart Beta策略指数作为风险资产输入CPPI类策略模型，构建最终投资组合，以期在实现超额收益的同时有效规避市场大幅下行风险，实现资产组合的保值增值。

本文的边际贡献方面，由于国内Smart Beta策略仍处于发展的初期，相关研究仍相对有限，且多集中于基于典型的Smart Beta价值、成长、规模、低波动性、动量、红利等单因子策略的应用性研究及因子择时研究方面，因此本文尝试采用的Smart Beta与CPPI综合策略，一方面能够拓展、丰富国内现有文献对Smart Beta策略、CPPI策略表现的实证研究，另一方面有助于探讨在利用Smart Beta策略时通过叠加CPPI类策略能否更加有效地规避市场性风险，跳出仅使用Smart Beta策略构建指数或仅使用CPPI类策略组合构建的单一思路，在目前黑天鹅事件频发、证券市场震荡加剧、系统性风险提升的大背景下，全球投资者避险需求急剧上升，冀望我们的研究能够为市场监管者和投资者提供一定参考。

二、文献综述

从1964 年Sharpe，Lintner，Mossin & Treyor 基于资产组合理论建立起资本资产定价模型（CAPM）以来，Beta 因子相区别于Alpha 因子出现在世人眼前。Haugen&Baker（1991）［5］基于对威尔逊5 000 指数在1972 至1989 年的研究证实了市场具有无效性，自此，学界对不同因子及如何构造最优风险资产组合展开了不懈的探索。Fama&French（1993）［6］、Fama&French（2014）［7］提出了FF 三因子模型、五因子模型，不断扩充因子库。

部分学者提出基本面指标可能比市值更可靠，Arnott et al.（2005）［8］通过对美国数据进行分析，提出可以使用部分基本面指标（如账面价值、收入、利润、分红等）进行加权，进而增强指数收益；Hemminki&Puttonen（2008）［9］对欧洲的研究发现，基于账面价值及分红构建的投资组合具有显著的超额收益。

此外，由于低波动率的市场异象一直存在（Xi et al.，2016［10］），部分学者从风险分散的角度出发，试图通过构建低波动率组合来降低组合的整体风险、实现夏普比率最大化，并由此衍生出等权重指数、最小波动率指数、风险平价指数、最大分散化指数等。Baker&Wurgler（2011）［11］发现低波动率组合及低Beta 组合实现了令人瞩目的平均收益，同时也拥有较小的回撤；Wei（2017）［12］通过情景分析发现，低波动率组合尤其适合养老金投资等应用场景，其既可以有效降低组合风险，又可以实现较高的夏普比率。

在A 股市场应用方面，Smart Beta 策略也具有较好投资效果。薛昆与魏江（2017）［13］通过研究发现四个风险分散类Smart Beta 策略指数均取得了高于基准指数的累计收益率及夏普比率；Cai et al.（2018）［14］的研究表明，基于上证50 成分股构建风险分散类Smart Beta 策略指数夏普比率均优于市值加权的上证50 指数。

固定比例投资组合保险策略（Constant Proportion Portfolio Insurance，CPPI）由Perold（1986）［15］、Perold&Sharpe（1988）［16］提出，最初应用于固定收益资产，旨在通过调整在无风险资产及风险资产间的资金分配比例，保证无论在何种市场条件下，在投资结束时资产组合价值均至少为本金的一定比例，实现投资组合保险目标；Black&Jones（1987［17］，1988［18］）将CPPI 策略扩展到了股票类资产。CPPI 策略的机制规则相较OBPI 策略更容易理解，且不需要通过利用期权等复杂衍生品进行组合构建，投资者可根据自身需要进行策略组合的灵活设定，故受到越来越多的投资管理人的关注与青睐，也成为较为主流的动态组合保险策略之一。杜少剑与陈伟忠（2005）［19］通过利用上证综指的实证研究发现，CPPI 策略在中国证券市场上可以起到一定的有效的保险作用。

鉴于CPPI 策略在规则设定时相对僵化，Estep&Kritzman（1988）［20］进一步提出了CPPI 策略的改进版本——非时变的资产组合保护策略（Time-invariant Portfolio Protection，TIPP）。在CPPI 策略的基础上，TIPP 策略通过调整预设的最低资产组合价值，保证最终资产组合价值既不会低于本金的一定比例，也不会低于资产组合所达到的最高价值的一定比例，可更好满足投资者希望保留更多收益的目标。

然而，部分学者发现，虽然在理论上相较其他策略具有较强的优越性，但在实际应用中，CPPI策略与TIPP 策略的结果不甚理想。越来越多的学者尝试对CPPI 策略及TIPP 策略进行优化；由于CPPI 策略及TIPP 策略中，固定的风险暴露通过乘数来决定，因此乘数是CPPI 及TIPP 策略中需要被确定的核心参数，如何更好地确定相关乘数也是一个可能的研究方向。Hamidi et al.（2009）［21］认为，非条件乘数没有充分考虑风险资产的风险变化情况，因此可以考虑使用根据市场情况的改变而改变的条件乘数。当市场处于牛市，风险资产价值迅速上升时，及时扩大乘数、提高风险暴露程度，有利于投资者更好地提升组合收益。姚远与郭珊（2012）［22］提出可以在每个调仓日根据前一期的股价变动对本期乘数进行灵活修正，从而更好地在上行期参与获利、下行期规避风险；Chen et al.（2008）［23］尝试利用遗传规划方法建立等式树，并结合主成分分析估计每期的乘数。也有部分学者指出，为了保证资产组合价值不跌破下限，乘数应与风险资产下一期的最大可能跌幅相关；在假设资产组合离散调仓的情况下，可以推导出乘数与在险价值（Value at Risk，VaR）的关系，即乘数为在险价值的倒数（Jiang et al.，2009［24］；Hamidi et al.，2014［25］）。进一步地，Hamidi et al.（2014）［25］指出，由于在险价值并不能反映最差情形中风险资产的损失情况，使用期望损失（Expected Shortfall，ES）替代在险价值，能够更好地衡量组合风险。

在近年来全球系统性风险上升的大背景下，基于Smart Beta 策略及CPPI 类策略的不同特性，部分海外学者也对两类策略的综合应用进行了实证研究。Theiler（2011）［26］通过利用历史模拟法对美国、欧洲指数进行分析发现，如果在Smart Beta 策略上叠加CPPI、TIPP 策略，可以达到及时止损的效果，明显提高组合的最终投资收益。Ardia et al.（2016）［27］通过对美国标普500 指数的相关研究也得出了类似的结论，发现Smart Beta 策略中等权重策略、低风险策略叠加CPPI、TIPP 策略应用，将带来比利用市值加权指数叠加CPPI、TIPP 策略所构建的组合更好的收益，策略的整体表现也更好。

相关学者的研究表明，Smart Beta 策略与CPPI 类策略的综合应用可能会带来更好的组合收益更好地控制组合风险。

目前A 股市场上综合策略应用的相关研究仍较少，因此本文将尝试综合使用Smart Beta 策略及CPPI 类策略构建投资组合，探索综合策略的应用是否会存在更好的表现。。

三、Smart Beta及CPPI类策略应用效果分析

（一）风险分散类Smart Beta策略

本文首先基于上证50指数以及其所有成分股的股价数据，测试了四类典型风险分散类Smart Beta策略指数：等权重策略指数、最小方差策略指数、风险平价策略指数、最大分散化指数的相关表现。

等权重策略是最简单、最基础的风险分散策略之一。假设投资组合中所含股票个数为n，则组合中每只股票的权重如下：

最小方差策略可看作均值方差最优化策略的调整版；在最小方差策略下，假设投资组合中所含股票个数为n，组合各个成分股的协方差矩阵为Ω，各股票的权重为wi，则组合中股票的权重向量w可通过如下的最优化过程得到：

风险平价策略的基本思想是保证每只股票对整体风险的贡献度相同。考虑到各个股票对可能具有不同的相关性后，定义总风险贡献为TRC（TotalRis k Contri b ution），则每只股票的总风险贡献TRCi应相同，即可通过求解如下最优化过程得到最优权重向量：

最大分散化策略的目标是构建能使组合风险得到最大分解的投资组合。假设组合的权重向量为w、标准差向量为σ，最大分散化策略等价于求解如下最优化过程：

在进行Smart Beta策略指数的编制时，首先需要确定调仓日期。考虑到较频繁地调仓需要较高成本，但调仓频率过低可能导致组合无法随着市场情况的变化进行及时调整的问题，故本文参考Bertrand，etal.（2002）［28］、Bertrand，etal.（2009）［29］等学者的做法，将调仓频率设置为月度，在每月月末依据策略规则进行各个股票的仓位调整。其次，进行最小方差策略、风险平价策略及最大分散化策略的应用均需要计算各股票的方差或投资组合内的所有股票的协方差矩阵。为了精确地对方差及协方差矩阵进行估计，本文使用每次调仓时点前一年的收益率数据进行计算。

本文将2006年1月1日设为基期，假设四个Smart Beta策略指数及上证50指数在基期的指数值均为1，所得Smart Beta策略指数从2006年1月1日至2018年12月28日的点数值如图1所示。表1展示了四个策略指数及上证50指数的相关年化指标，无风险利率取为1个月中债国债到期收益率在对应区间的均值。在回测区间内，风险分散类的Smart Beta策略指数无论是年化收益还是夏普比率相比较均明显优于上证50指数，且最小方差策略指数、风险平价策略指数在实际应用中效果较好。同时，在2015年股灾爆发后的阶段，最小方差策略指数的收益表现明显优于其他几类指数，其指数数值与其他指数的差距不断扩大，最终达到了极高的点位值，体现了该策略较好的收益增强作用。

但也应注意到，四种风险分散类的Smart Beta策略指数与上证50指数的整体演进趋势相对较为一致；从最大回撤来看，除最小方差策略指数的最大回撤为63.20%明显较低外，等权重、风险平价、最大分散化策略指数的最大回撤分别为72.88%、71.84%、72.79%，与上证50指数72.41%的回撤较为接近，体现出风险分散类的Smart Beta策略指数仍面临的较大系统性风险，侧面反映了综合应用相关策略的现实意义。

图1 四类Smart Beta策略指数及上证50指数点位变化情况

表1 四类Smart Beta策略指数及上证50指数相关统计指标

（二）CPPI类策略

传统CPPI策略事先确定本金保护比例及决定了风险暴露程度的核心变量——乘数。假设投资组合初始价值为V0，投资组合的初始下限为F0，无风险利率为rf，整个投资期限为［0，T］，本金保护比例为η，则通常投资组合的初始下限与组合价值间满足如下关系式：

假设初始投资于风险资产的价值为F0，投资于无风险资产的价值为P0，乘数为m；定义缓冲层（C）为资产价值与资产下限之差，CPPI模型的核心假设为投资于风险资产的价值与乘数及缓冲层C成正比。在［0，T］时间内，任意时刻t，投资者应用如下公式进行仓位调整：

标准TIPP策略为满足投资者希望保留投资过程中的最高收益的一定比例的现实需求，定义将新的下限定义如下：

由于标准TIPP策略是标准CPPI策略的简单改进版本，故其也遵循CPPI策略的基本框架。在投资期限内的任意时刻t，TIPP策略下调仓规则可用下列表达式进行描述，其中各符号含义与前文中所述的CPPI策略中的符号含义相同：

本文首先对标准CPPI及TIPP策略组合的实际应用效果进行对比分析。在实际应用中，常数乘数 m 的取值范围一般为［1，13］（Bertrand，etal.，2009［29］），因此，本文将乘数分别取为 3、6、9、12，对两类策略进行测试。假设投资起始日为2007年1月1日，在起始日分别构建乘数为3、6、9、12的4个标准CPPI投资组合及4个标准TIPP投资组合，其中本金保护比例η为90%，组合的初始价值为1 000；每月月末进行调仓，持有这些组合至2018年12月28日，计算这些投资组合在投资期内的每日的价值，可以得到在整个期间投资组合的价值演进曲线。图2展示了这8个策略组合在整个投资期间内的价值变化情况，表2展示了上证50指数及8个投资组合的相关统计指标。

可以明显看出，当2008年金融危机、2015年股灾等较大的系统性风险爆发时，由于TIPP策略下的投资组合在构建过程中由于将组合价值的下限定义为本金的一定比例与资产组合所达到的最高价值的一定比例中的较大值，所以在危机爆发的相对初期即触碰到了组合价值的下限，进而将资产全部投入无风险资产，较好地规避了系统性风险所引起的组合价值的大幅下跌，其表现明显好于标准CPPI策略；最终CPPI策略下的四个投资组合的表现甚至相较上证50指数更差，投资期末出现了本金的亏损。标准差及最大回撤的结果也均体现出了TIPP策略组合相较于CPPI策略组合的优越性。故在下文的分析中，本文将集中于TIPP策略应用的相关探索。

图2 常数CPPI、TIPP策略组合及上证50指数组合价值变化情况（2007年1月1日—2018年12月28日）

表2 常数CPPI、TIPP策略组合及上证50指数组合相关统计指标（2007年1月1日—2018年12月28日）

由于标准TIPP策略在整个投资期限内乘数保持不变，可能并未充分考虑随时间推移风险资产的价格及风险的变化情况，因此寻找根据市场情况的改变而改变的条件乘数，可能有助于更好地把控组合风险、提高资产组合的表现。本文将参考相关学者的研究，应用其中的两类条件乘数估计方法进行测试。

1.条件乘数的收益率调整法

姚远和郭珊（2012）［22］提出了条件乘数的收益率调整法，即考虑到短期可能存在的动量效应，可以考虑在每个调仓日利用上一期的风险资产价值的变动对本期的乘数进行相关修正，进而更好地达到在价格上行期获利、下行期规避风险的目的，具体公式如下：

其中a（a≥1）为乘数扩大器，取决于投资者的风险偏好；a的取值一般为1、2、3、4等整数，较大的a会导致投资组合对风险资产的价值变动更加敏感，将会针对市场情况的变化对风险资产进行更大幅度的调整。在本文中，假设投资者的风险偏好为较低水平，乘数扩大器a的取值为2。通过公式（9）可以看出，股价的上行将会带来条件乘数向上修正，从而试图通过增加风险暴露程度更多地从市场的上涨中获利；股价的下行将会带来条件乘数向下修正，从而试图通过减少风险暴露程度规避系统性风险。

2.条件乘数的ES估计法

除了利用上一期风险资产的价格变动来估计条件乘数外，部分学者（Jiang etal.，2009［24］；Hamidi，etal.，2014［25］）指出，乘数与在险价值间存在一定的关系；Hamidi，etal.（2014）［25］指出，由于在险价值并不能反映在最差情形中风险资产的损失情况，使用期望损失（ES）替代在险价值能够更好地衡量组合风险，从而提出了条件乘数的ES估计法。本文参考上述学者的研究，考虑利用期望损失来估计条件乘数，具体公式如下：

接下来，条件乘数的估计问题转为期望损失ES的估计问题。一般而言，常用的分位数估计法有非参数法、参数法、半参数法等；由于半参数法中GARCH估计法考虑到了资产收益率所存在的波动率群集现象，部分学者认为利用GARCH（1，1）模型对下一期的波动率进行估计将会得到更好的估计效果①MANGANELLI，et al.Value at risk models in finance （August 2001）［EB/OL］.ECBWorking Paper No.75.Available at SSRN：https：//ssrn.com/abstract=356220.。本文同时考虑到资产收益率序列可能存在的时间序列自相关情况，如果在每个调仓日利用AIC或者BIC规则筛选出最合适的ARMA模型，并综合利用ARMA+GARCH（1，1）模型对资产收益率的条件均值及方差进行预测，可能会实现更好的效果。具体而言，假设资产收益率服从t分布，在每个调仓日首先拟合ARMA（pM，qM）+GARCH（1，1）模型，其中ARMA 模型的阶数由 AIC规则来进行确定；利用拟合出的模型即可预测下一期的均值及方差，作为t分布的相关参数，再估计期望损失，因此下面需推导t分布下期望损失的表达式。

假设资产收益率服从均值为μ，方差为σ2，自由度为n的t分布，设伽马函数为G（.），则标准t分布的概率密度函数可表达为：

根据定义式，可以得到在标准正态分布下，期望损失的表达式可以具体推导如下：

因此，在标准t分布下，期望损失ES是在险价值VaR的函数。

设t1为均值为μ，方差为σ的非标准t分布，t0为标准t分布，则有：

因而可得非标准t分布的在险价值与标准t分布的在险价值间的关系式如下：

下面利用期望损失的定义式，推导非标准t分布的期望损失与标准t分布的期望损失间的关系：

因此，本文在计算非标准t分布的期望损失时，将首先计算标准t分布的在险价值，继而利用公式（12）求出标准t分布的期望损失，最后利用公式（15）求出非标准t分布的期望损失。在估计出期望损失之后，再利用乘数与期望损失的关系式（10），即可求出条件乘数，进而进行投资组合的构建与仓位调整。

本文分别按照乘数为3、6、9、12的常数乘数TIPP策略规则及条件乘数的收益率调整法、条件乘数的ES估计法两类条件乘数确定方法，基于上证50指数，构建投资期为2011年1月1日至2018年12月28日、月末调仓、本金保护比例η=90%，组合的初始价值为1 000的投资组合，所得各个投资组合的价值变化情况如图3所示，表4展示了相关统计指标。回测表明，两个条件乘数策略及乘数为12、9的TIPP策略具有较好的综合投资效果；而乘数为3、6的TIPP策略则虽具有较为明显的低波动性特征，但从夏普比率来看表现较差。因此，下文使用两个条件乘数TIPP策略及乘数为9、12的TIPP策略，与Smart Beta策略进行综合应用。

图3 常数及条件乘数TIPP策略组合及上证50指数组合价值变化情况（2011年1月1日—2018年12月28日）

表3 常数及条件乘数TIPP策略组合及上证50指数组合相关统计指标（2011年1月1日—2018年12月28日）

四、Smart Beta及CPPI类策略的综合应用效果分析

基于此前分析，风险分散类的Smart Beta策略指数中最小方差策略指数、风险平价策略指数在实际应用中效果较好；TIPP策略的实际应用效果好于CPPI策略的应用效果，且其中两类条件乘数TIPP策略及乘数为9、12的常数乘数TIPP策略表现相对较好。因此接下来，本文将尝试把之前计算中所得到的最小方差策略指数、风险平价策略指数这两类策略指数分别作为风险资产输入TIPP策略的构建框架中，并分别应用两类条件乘数估计法及两个常数乘数，以实现Smart Beta及CPPI类策略的综合应用，观察8种可能的方法组合中哪种方法可能会达到较好的效果。为了方便下文叙述，本文将8个Smart Beta及TIPP综合策略组合进行了编号，表4展示了各个综合策略的相关信息。

表4 8个Smart Beta及TIPP综合策略相关编号

8个Smart Beta及TIPP综合策略组合的投资期间为2011年1月1日至2018年12月28日，本金保护比例η为90%，组合的初始价值为1 000，图4为最终所得到的组合价值变化情况的结果，表5为各组合相关统计指标。可以看出，通过在2015年股灾爆发前充分投资于风险资产，并在市场出现大幅下行时及时通过将资产全部投入无风险资产进行止损，8个综合策略组合的投资收益均显著优于上证50指数的收益，夏普比率也均高于上证50指数，表明综合策略的应用相较单纯的市值加权指数确实具有更好的效果。

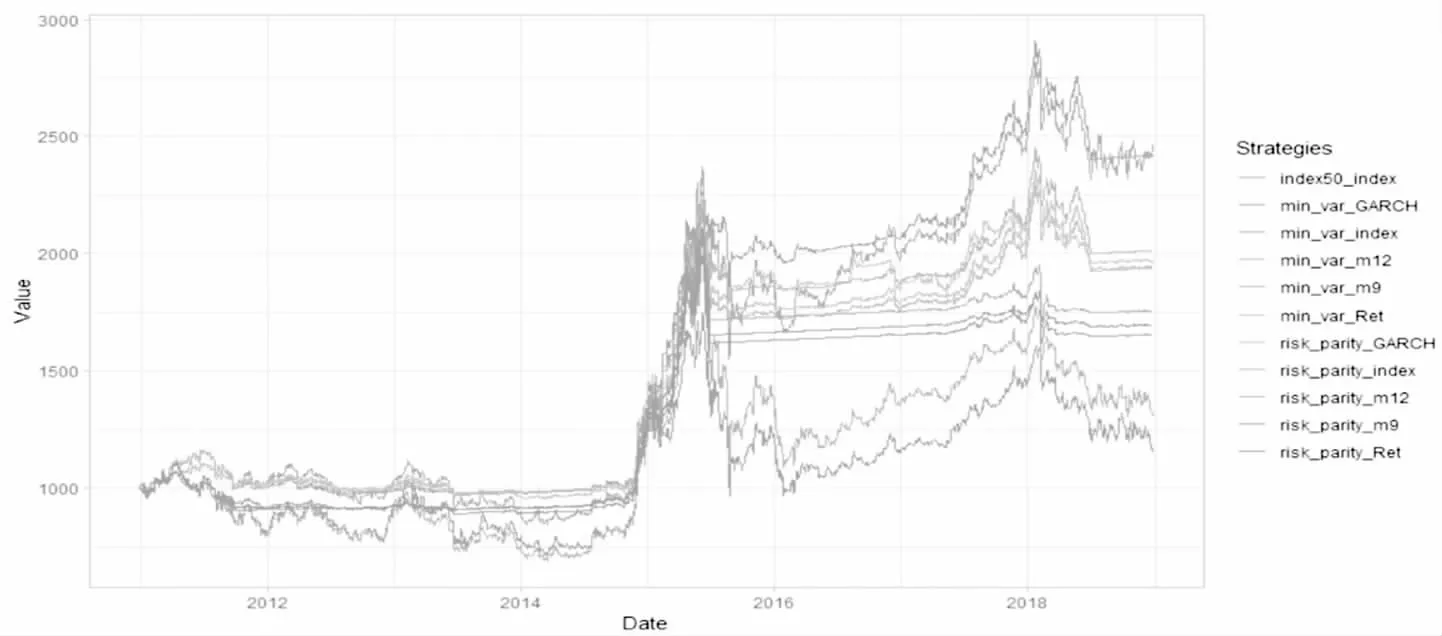
图4 Smart Beta策略及TIPP策略综合应用组合价值变化情况（本金保护比例为90%）

从8个综合策略投资组合的相关统计指标来看，综合策略5具有最高的年化收益率，为12.02%，体现出明显的高收益特征；综合策略1、综合策略8收益表现也相对较好，分别为9.63%、9.61%。从波动性来看，8个综合策略组合的标准差均小于13%，远低于2个策略指数及上证50指数，且综合策略1、综合策略5下的投资组合具有最低的波动性，标准差分别为9.95%、10.06%。从夏普比率来看，由于E S估计法下的TIPP策略能够在平抑组合风险的前提下有效保证组合收益，其与最小方差策略指数、风险平价策略指数的综合应用取得了最高的夏普比率值，分别为0.963、0.734。

表5 Smart Beta策略及TIPP策略综合应用组合相关统计指标（本金保护比例为90%）

此外，在不同的Smart Beta策略指数上叠加TIPP策略所取得的增强效果并不相同。为了更好地进行观察，图5、图6分别绘制了在风险平价策略指数、最小方差策略指数叠加四个TIPP策略的效果。

对于风险平价策略指数而言，综合策略的叠加应用无论在收益增强方面还是在稳定性提高方面，均取得了良好效果。从年化收益率来看，风险平价策略指数的平均收益率仅为3.53%，但综合策略1、4、3、2下的投资组合的平均收益率分别为9.63%、8.37%、7.14%、6.48%，体现出了较好的收益增强效果。从波动率来看，TIPP策略的叠加使用也均降低了组合的波动性，风险平价策略指数的波动率为22.98%，而四个综合策略的波动率均低于12%，组合稳定性显著提升。最大回撤方面，与TIPP策略在最小方差策略指数上综合应用所得的估计结果类似，E S估计法下的综合策略1最大回撤最小，仅为12.67%；综合策略2、4、3下组合的最大回撤分别为22.83%、22.83%、20.67%，具有相对较大的缺口风险，但仍大大低于风险平价策略指数45.51%的最大回撤。由于四个综合策略组合均起到了有效的收益增强及波动性平抑效果，其夏普比率远高于风险平价策略指数的0.052，综合策略1、4、3、2下的组合的夏普比率分别为0.734、0.527、0.471、0.356。从偏度来看，除综合策略1下的日收益率轻微正偏，偏度为0.194外，其他投资组合的及指数均体现出轻微的负偏特征，而这也于金融市场收益率的经验统计结果相一致；从峰度来看，风险平价策略指数组合的峰度为5.886，但四个综合策略组合的峰度均超过15，体现出明显的尖峰特点。

图5 风险平价策略指数及TIPP策略综合应用组合价值变化（本金保护比例为90%）

对于最小方差策略指数而言，由于该指数本身就具有较高收益性及较好的风险规避能力，年化收益率高达11.88%，而在叠加TIPP策略的过程中，组合会将部分资产投资于收益率较低的无风险资产以降低组合风险，因此TIPP策略的叠加对收益可能会产生一定的负面影响。从年化收益率来看，除了综合策略5收益率为12.02%略高于最小方差策略指数组合外，其他几个组合的年化收益率均低于最小方差策略指数，综合策略6、7、8的年化收益率分别为8.63%和8.16%、9.61%。然而，TIPP策略的叠加使用显著降低了组合的波动性，最小方差策略指数的波动率为19.22%，而四个综合策略组合的波动率均低于13%，体现出了较好的风险分散效应。同时，通过观察可以发现，E S估计法下的综合策略组合实现了对最小方差策略指数的较好跟踪，不仅取得了与其极为接近的收益，而且较好地降低了组合的波动性，从而导致了投资组合夏普比率的大幅提升。最大回撤方面，综合策略5的最大回撤最小，仅为12.05%；综合策略6、7、8下投资组合的最大回撤分别为19.25%、22.89%、21.25%，体现出了较大的缺口风险，但所有组合的最大回撤均明显小于最小方差策略指数组合的最大回撤34.60%。得益于叠加TIPP策略后组合稳定性的明显增强，四个综合策略组合的夏普比率均高于最小方差策略指数组合的夏普比率，从高到低排序分别为综合策略5、6、8、7下的投资组合，夏普比率分别为0.963、0.614、0.547和0.501。偏度及峰度方面所得结果与TIPP策略在风险平价策略指数上综合应用所得结果也较为类似。

图6 最小方差策略指数及TIPP策略综合应用组合价值变化（本金保护比例为90%）

通过综合分析可以看出，综合策略5——最小方差策略与E S估计法下的条件乘数TIPP策略的叠加使用所得投资结果最好，不仅能够取得较好的收益，而且能够同时保持组合的相对稳定性，最大回撤较小、夏普比率最高，在各个综合策略组合中的表现最为良好；从夏普比率来看，综合策略1——风险平价与E S估计法下的TIPP综合策略组合、综合策略8——最小方差与乘数为12的TIPP综合策略组合、综合策略7——最小方差与乘数为9的TIPP综合策略组合也具有较为不错的表现。

考虑到不同的投资者由于风险偏好及风险承受能力不同，在投资期初设定的本金保护比例也可能存在差异，为了进一步验证在不同的本金保护比例下综合策略组合的效果是否稳健，本文将本金保护比例η设定为85%，再次构建上述投资组合，组合价值变化情况如图7所示，表6展示了相关统计指标。图8、图9再次分别绘制了在风险平价策略指数、最小方差策略指数上叠加四个TIPP策略的效果。最终所得结果与本金保护比例η=90%的结果较为类似，体现了本文结论的相对稳健性。

图7 Smart Beta策略及TIPP策略综合应用组合价值变化情况（本金保护比例为85%）

表6 Smart Beta策略及TIPP策略综合应用组合相关统计指标（2011年1月1日—2018年12月28日，本金保护比例为85%）

图8 风险平价策略指数及TIPP策略综合应用组合价值变化（本金保护比例为85%）

图9 最小方差策略指数及TIPP策略综合应用组合价值变化（本金保护比例为85%）

五、结论与投资建议

在全球局势震荡加剧、股市系统性风险上升的大背景下，本文基于上证50指数及其成分股股价数据的研究发现，综合应用风险分散类的Smart Beta策略及CPPI类策略确实能够综合利用两者优点，在实现超额收益的同时有效规避市场大幅下行风险，达到更好的投资效果。

本文对四个风险分散类Smart Beta策略进行测试表明，此类策略能够起到收益增强效果，其中最小方差策略指数兼具高收益性及低波动性特征，其表现最优，风险平价策略指数也具有不错的表现；但当系统性风险爆发时，指数组合还是会较多地受到市场整体下行的负面影响，出现较大幅度的回撤。对标准CPPI及TIPP策略组合的实际应用效果进行分析，可以发现TIPP策略整体更优；分析条件乘数及常数乘数TIPP策略组合相关表现，可以看到收益率调整法、E S估计法下的条件乘数策略及乘数为12、9的TIPP策略具有较好的综合投资效果。因此，本文使用两个条件乘数TIPP策略及乘数为9、12的TIPP策略，与Smart Beta策略中最小方差策略指数、风险平价策略指数进行综合应用。

实证结果表明，综合策略的应用相较单纯的市值加权指数确实具有更好的效果。其中，最小方差策略与E S估计法下的条件乘数TIPP策略的叠加使用所得投资结果最好，可以起到对最小方差策略指数的较好跟踪效果，同时明显降低组合的波动性，进而同时实现较好投资收益及保持组合相对稳定的双重投资目标；夏普比率最高、最大回撤较小。夏普比率测度下，风险平价与E S估计法下的TIPP综合策略组合、最小方差与乘数为12的TIPP综合策略组合、最小方差与乘数为9的TIPP综合策略组合也具有较为不错的表现。

此外，在不同的Smart Beta策略指数上叠加TIPP策略所取得的增强效果并不相同。对于最小方差策略指数而言，由于该指数本身就具有较高收益性及较好的风险规避能力，而在叠加TIPP策略的过程中组合会将部分资产投资于收益率较低的无风险资产以降低组合风险，因此TIPP策略的叠加对收益可能会产生一定的负面影响，除了ES估计法下的综合策略组合的收益率略高于最小方差策略指数组合外，其他几个组合的年化收益率均低于最小方差策略指数；但TIPP策略的叠加使用显著降低了组合的波动性，使得最终四个综合策略组合的夏普比率均高于最小方差策略指数组合的夏普比率。对于风险平价策略指数而言，综合策略的叠加应用无论在收益增强方面还是在稳定性提高方面均取得了良好效果，综合策略组合的夏普比率远高于风险平价策略指数。

为了进一步验证在不同的本金保护比例下综合策略组合的效果是否稳健，本文将本金保护比例η设定为85%，再次构建投资期限为2011—2018年8个综合策略投资组合。最终所得结果与η=90%时的结果也较为一致，体现了策略的相对稳健性。

基于上述分析，本文的主要结论及投资建议如下：

（1）对于单纯的指数投资者而言，风险分散类Smart Beta指数相较上证50指数确实具有一定的超额收益，其中最小方差策略指数表现最优，风险平价策略指数也为较好选择；

（2）对比CPPI类投资组合保险策略，TIPP策略相较CPPI策略收益更好、组合稳定性更强；在TIPP策略中，E S估计法下的条件乘数TIPP策略表现最优，乘数为12、乘数为9的标准TIPP策略、收益率调整法下的条件乘数TIPP策略的表现也相对较好。

（3）Smart Beta策略与CPPI类策略的综合应用确实能够起到相较单一策略应用更好的投资效果，其中最小方差策略与E S估计法下的条件乘数TIPP策略的叠加使用所得投资结果最好，可以同时实现较好投资收益及保持组合相对稳定的双重投资目标。此外，风险平价与E S估计法下的TIPP综合策略组合、最小方差与乘数为12、9的TIPP综合策略组合也具有较为不错的表现。